Test t dla próbek sparowanych: definicja, wzór i przykład

Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.

W tym samouczku wyjaśniono następujące kwestie:

• Motywacja do wykonania testu t dla par próbek.
• Wzór na wykonanie testu t dla par próbek.
• Założenia, które należy spełnić, aby przeprowadzić test t dla par próbek.
• Przykład wykonania testu t dla par próbek.

Test t dla par prób: Motywacja

Test t dla par próbek jest powszechnie stosowany w dwóch scenariuszach:

1. Pomiaru dokonuje się na pacjencie przed i po zabiegu – np. mierzony jest maksymalny skok pionowy zawodników koszykówki z college’u przed i po ich udziale w programie treningowym.

2. Pomiaru dokonuje się w dwóch różnych warunkach – na przykład czas reakcji pacjenta mierzony jest w przypadku dwóch różnych leków.

W obu przypadkach chcemy porównać średni pomiar pomiędzy dwiema grupami, w którym każdą obserwację z jednej próby można powiązać z obserwacją z drugiej próby.

Test t dla sparowanych próbek: wzór

Test t dla par prób zawsze wykorzystuje następującą hipotezę zerową:

• H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)

Hipoteza alternatywna może być dwustronna, lewa lub prawa:

• H ₁ (dwustronny): μ ₁ ≠ μ ₂ (średnie z dwóch populacji nie są równe)
• H ₁ (po lewej): μ ₁ < μ ₂ (średnia populacji 1 jest niższa niż średnia populacji 2)
• H ₁ (po prawej): μ ₁ > μ ₂ (średnia populacji 1 jest większa niż średnia populacji 2)

Do obliczenia statystyki testu t używamy następującego wzoru:

t = x _różnica / (s _różnica /√n)

Złoto:

• x _diff : przykład średniej różnic
• s: przykład odchylenia standardowego różnic
• n: wielkość próby (tj. liczba par)

Jeśli wartość p odpowiadająca statystyce testu t z (n-1) stopniami swobody jest mniejsza niż wybrany poziom istotności (najczęściej wybierane są 0,10, 0,05 i 0,01), wówczas można odrzucić hipotezę zerową.

Test t dla sparowanych próbek: założenia

Aby wyniki testu t dla par próbek były ważne, muszą zostać spełnione następujące założenia:

• Uczestnicy powinni być wybierani losowo z populacji.
• Różnice między parami powinny mieć w przybliżeniu rozkład normalny.
• W różnicach nie powinny występować skrajne wartości odstające.

Test t dla sparowanych próbek : przykład

Załóżmy, że chcemy wiedzieć, czy określony program treningowy jest w stanie zwiększyć maksymalny skok w pionie (w calach) u koszykarzy z college’u.

Aby to przetestować, możemy wybrać prostą losową próbę 20 koszykarzy z college’u i zmierzyć każdy z ich maksymalnych skoków w pionie. Następnie możemy pozwolić każdemu zawodnikowi korzystać z programu treningowego przez miesiąc, a następnie pod koniec miesiąca ponownie zmierzyć jego maksymalny skok wzwyż.

Aby ustalić, czy program treningowy rzeczywiście miał wpływ na maksymalny skok w pionie, przeprowadzimy test t dla sparowanych próbek na poziomie istotności α = 0,05, wykonując następujące kroki:

Krok 1: Oblicz podsumowanie danych dla różnic.

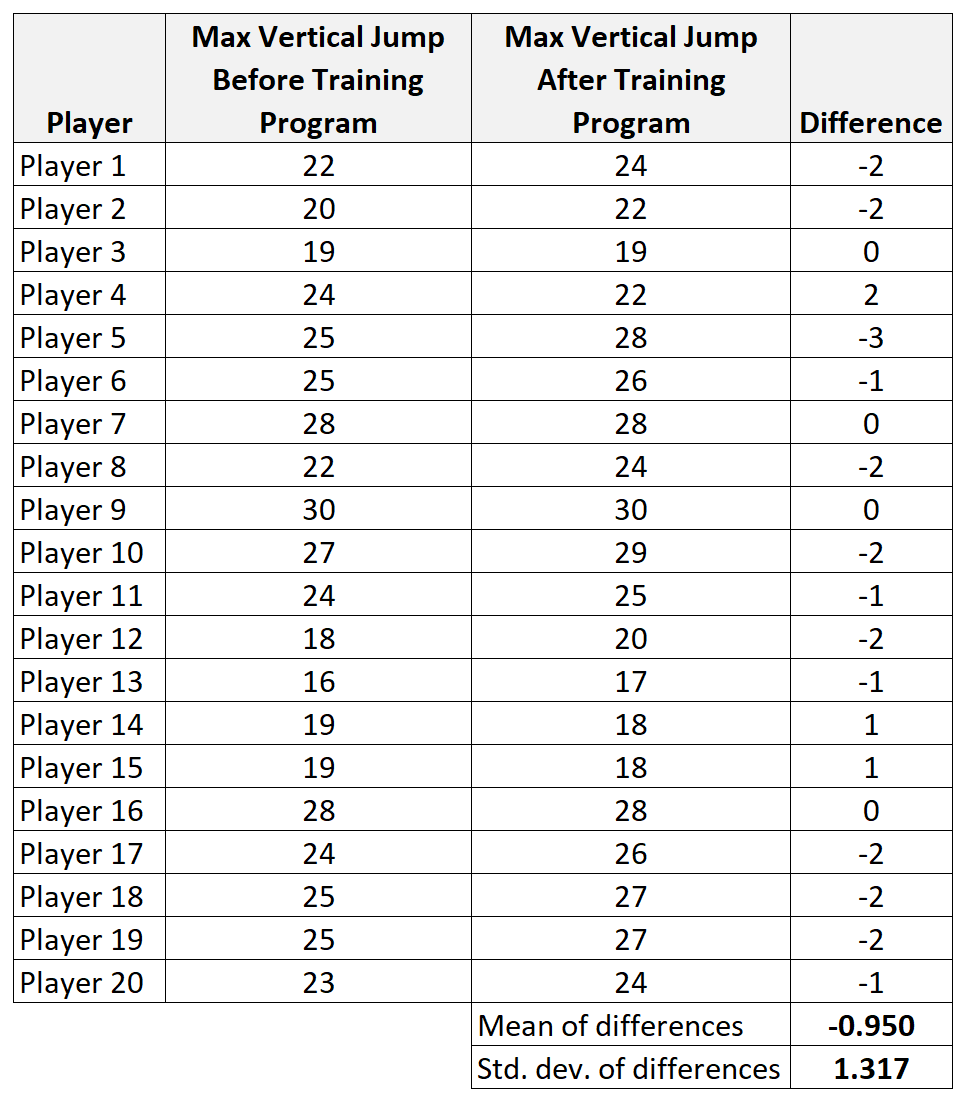
• x _diff : średnia z prób różnic = -0,95
• s: odchylenie standardowe próby różnic = 1,317
• n: wielkość próby (tj. liczba par) = 20

Krok 2: Zdefiniuj założenia.

Test t przeprowadzimy dla sparowanych próbek przy następujących hipotezach:

• H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)
• H ₁ : μ ₁ ≠ μ ₂ (średnie z obu populacji nie są równe)

Krok 3: Oblicz statystykę testu t .

t = x _różnica / (s _różnica /√n) = -0,95 / (1,317/ √ 20) = -3,226

Krok 4: Oblicz wartość p statystyki testu t .

Według kalkulatora wyniku T do wartości P , wartość p związana z t = -3,226 i stopniami swobody = n-1 = 20-1 = 19 wynosi 0,00445 .

Krok 5: Wyciągnij wnioski.

Ponieważ ta wartość p jest poniżej naszego poziomu istotności α = 0,05, odrzucamy hipotezę zerową. Mamy wystarczające dowody, aby stwierdzić, że średni maksymalny skok pionowy zawodników różni się przed i po wzięciu udziału w programie treningowym.

Uwaga: Można także wykonać cały test t dla prób zależnych, korzystając po prostu z kalkulatora testu t dla prób zależnych .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak przeprowadzić test t dla par próbek przy użyciu różnych programów statystycznych:

Jak wykonać test t dla par próbek w programie Excel
Jak wykonać test t dla sparowanych próbek w SPSS
Jak wykonać test t dla sparowanych próbek w Stata
Jak wykonać test t dla sparowanych próbek na kalkulatorze TI-84
Jak wykonać test t dla sparowanych próbek w R
Jak wykonać test t dla sparowanych próbek w Pythonie
Jak ręcznie wykonać test T dla par próbek