Test t-studenta

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest test t-Studenta i do czego służy w statystyce. W ten sposób dowiesz się, jak przeprowadzany jest test t-Studenta, jakie są różne rodzaje testów t-Studenta i jaki jest na nie wzór.

Co to jest test t-Studenta?

Test t-Studenta , zwany także testem T lub po prostu testem t , jest testem statystycznym, w którym statystyka testowa jest zgodna z rozkładem t-Studenta . Dlatego w statystyce test t-Studenta służy do odrzucenia lub przyjęcia hipotezy zerowej testu hipotezy.

W szczególności test t-Studenta jest używany do testowania hipotez , w którym badana populacja ma rozkład normalny, ale wielkość próby jest zbyt mała, aby poznać wariancję populacji.

Krótko mówiąc, test t-Studenta służy do odrzucenia lub przyjęcia hipotezy badawczej niektórych testów hipotez. Na przykład test t-Studenta służy do testowania hipotez dla jednej próby, dla prób niezależnych lub dla prób pokrewnych. Następnie zobaczymy, jak w każdym przypadku obliczany jest test t-Studenta.

Rodzaje testów t-Studenta

Istnieją trzy rodzaje testów t-Studenta :

Test t-Studenta dla jednej próby – służy do sprawdzenia hipotezy o wartości średniej z próby.
Test t-Studenta dla dwóch niezależnych prób : pozwala sprawdzić hipotezę o różnicy średnich z dwóch niezależnych próbek.
Test t-Studenta dla dwóch sparowanych próbek (lub próbek pokrewnych) – służy do sprawdzenia hipotezy o średniej z próbki badanej dwukrotnie.

Przykład testu t-Studenta

Testy hipotez dla średniej próby to takie, w których hipoteza zerowa i hipoteza alternatywna testu mówią coś o wartości średniej populacji.

Wzór na test t-Studenta dla jednej próby jest następujący:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Złoto:

$t$

jest statystyką testu hipotezy dla średniej, która jest zdefiniowana przez rozkład t-Studenta.
$\overline{x}$

to przykładowe środki.
$\mu$

jest wartością średniej zaproponowanej w teście hipotezy.
$s$

jest odchyleniem standardowym próbki.
$n$

to wielkość próbki.

Po obliczeniu wartości testu t-Studenta wynik testu statystycznego z wartością krytyczną należy zinterpretować tak, aby odrzucić lub nie hipotezę zerową:

Jeżeli test hipotezy dla średniej jest dwustronny, hipotezę zerową odrzuca się, jeśli wartość bezwzględna testu t-Studenta jest większa od wartości krytycznej t _α/2|n-1 .
Jeżeli test hipotezy dla średniej odpowiada prawemu ogonowi, hipoteza zerowa zostaje odrzucona, jeśli wartość testu t-Studenta jest większa niż wartość krytyczna t _α|n-1 .
Jeśli test hipotezy dla średniej odpowiada lewemu ogonowi, hipoteza zerowa zostaje odrzucona, jeśli wartość testu t-Studenta jest mniejsza niż wartość krytyczna -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Należy pamiętać, że krytyczne wartości testowe uzyskuje się z tabeli rozkładu Studenta.

➤ Zobacz: Konkretny przykład testowania hipotezy dla średniej

Test t-Studenta dla prób niezależnych

Test t-Studenta dla prób niezależnych służy do odrzucenia lub przyjęcia hipotezy o związku pomiędzy średnimi dwóch populacji, na przykład, że średnie z dwóch populacji są różne lub że średnia populacji A jest większa od średniej . populacja B.

Jednakże w tym przypadku wzór na test t-Studenta zmienia się w zależności od tego, czy można założyć, że wariancje populacji są równe, czy nie. Zobaczymy wówczas dwa możliwe przypadki.

Nieznane i równe odchylenia

Wzór na obliczenie testu t-Studenta dla prób niezależnych, gdy wariancje populacji są nieznane, ale zakłada się, że są równe, jest następujący:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Złoto:

$t$

jest statystyką testującą hipotezę dotyczącą różnicy średnich o nieznanych wariancjach, która jest zgodna z rozkładem t-Studenta z n ₁ + n ₂ -2 stopniami swobody.
$\mu_1$

jest średnią populacji 1.
$\mu_2$

jest średnią populacji 2.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$s_p$

jest zbiorczym odchyleniem standardowym.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Łączne odchylenie standardowe dwóch próbek oblicza się przy użyciu następującego wzoru:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Nieznane i różne odmiany

Jeżeli wariancje populacji nie są znane, a ponadto zakłada się, że są różne, wzór na obliczenie testu t-Studenta dla prób niezależnych jest następujący:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Złoto:

$t$

jest statystyką testującą hipotezę dotyczącą różnicy średnich o nieznanych wariancjach, która jest zgodna z rozkładem t-Studenta.
$\mu_1$

jest średnią populacji 1.
$\mu_2$

jest średnią populacji 2.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$\sigma_1$

jest odchyleniem standardowym populacji 1.
$\sigma_2$

jest odchyleniem standardowym populacji 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Jednakże w tym przypadku stopnie swobody rozkładu t-Studenta obliczane są ze wzoru:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Zobacz: Konkretny przykład testowania hipotez pod kątem różnicy średnich

Test t-Studenta dla próbek sparowanych lub powiązanych

Test ten stosuje się, gdy dwie badane próbki są ze sobą powiązane, tak że w rzeczywistości jest to pojedyncza próbka osobników, która została poddana analizie dwukrotnie (za każdym razem w innych warunkach).

Można na przykład analizować oceny uczniów z zajęć z matematyki i statystyki, aby sprawdzić, czy istnieje znacząca różnica między średnimi z obu przedmiotów. W tym przypadku ocena z matematyki każdego ucznia jest powiązana z oceną ze statystyki tego samego ucznia.

Wzór testu t-Studenta dla próbek sparowanych lub powiązanych to:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

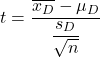
Złoto:

$t$

jest statystyką testującą hipotezę dla sparowanych średnich, która jest zdefiniowana przez rozkład t-Studenta.
$\overline{x_D}$

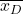
jest średnią próbki utworzoną na podstawie różnicy danych.
$\mu_D$

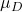
jest wartością średniej zaproponowanej w teście hipotezy.
$s_D$

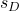
jest odchyleniem standardowym próbki utworzonym przez różnicę danych.
$n$

to wielkość próbki.

Założenia testu t-Studenta

Aby wykonać test t-Studenta muszą zostać spełnione następujące warunki:

Ciągłość – przykładowe dane są ciągłe.
Losowość : Próbki danych zostały wybrane losowo.
Homogeniczność : wariancja próbki danych jest jednorodna.
Normalność – rozkład definiujący próbkę danych jest w przybliżeniu normalny.

Jak wykonać test t-Studenta

Na koniec, podsumowując, szczegółowo opisano kroki, które należy wykonać, aby przeprowadzić test t-Studenta.

Zdefiniuj hipotezę zerową i alternatywną podczas testowania hipotez.
Ustal poziom istotności (α) testu hipotezy.
Sprawdź, czy spełnione są założenia testu t-Studenta.
Zastosuj odpowiedni wzór na test t-Studenta i oblicz statystykę testową.
Zinterpretuj wynik testu t-Studenta, porównując go z wartością krytyczną testu.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Co to jest test t-Studenta?

Rodzaje testów t-Studenta

Przykład testu t-Studenta

Test t-Studenta dla prób niezależnych

Nieznane i równe odchylenia

Nieznane i różne odmiany

Test t-Studenta dla próbek sparowanych lub powiązanych

Założenia testu t-Studenta

Jak wykonać test t-Studenta

o autorze

Dr Benjamin Anderson

Dodaj komentarz