Jak wykonać test t welcha w r

Test t Welcha służy do porównywania średnich między dwiema niezależnymi grupami, gdy nie zakłada się, że obie grupy mają równe wariancje.

Aby wykonać test t Welcha w R, możemy użyć funkcji t.test() , która wykorzystuje następującą składnię:

t.test(x, y, alternatywa = c(„dwie twarze”, „mniej”, „większy”))

Złoto:

• x: wektor liczbowy wartości danych dla pierwszej grupy
• y: wektor numeryczny wartości danych dla drugiej grupy
• alternatywa: alternatywna hipoteza testu. Domyślnie jest dwustronny.

Poniższy przykład pokazuje, jak użyć tej funkcji do wykonania testu t Welcha w R.

Przykład: test t Welcha w R

Nauczyciel chce porównać wyniki egzaminów 12 uczniów, którzy korzystali z broszury przygotowującej do egzaminu w celu przygotowania się do egzaminu, z wynikami 12 uczniów, którzy tego nie robili.

Poniższe wektory przedstawiają wyniki egzaminów uczniów w poszczególnych grupach:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Przed wykonaniem testu t Welcha możemy najpierw utworzyć wykresy pudełkowe , aby zwizualizować rozkład wyników dla każdej grupy:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

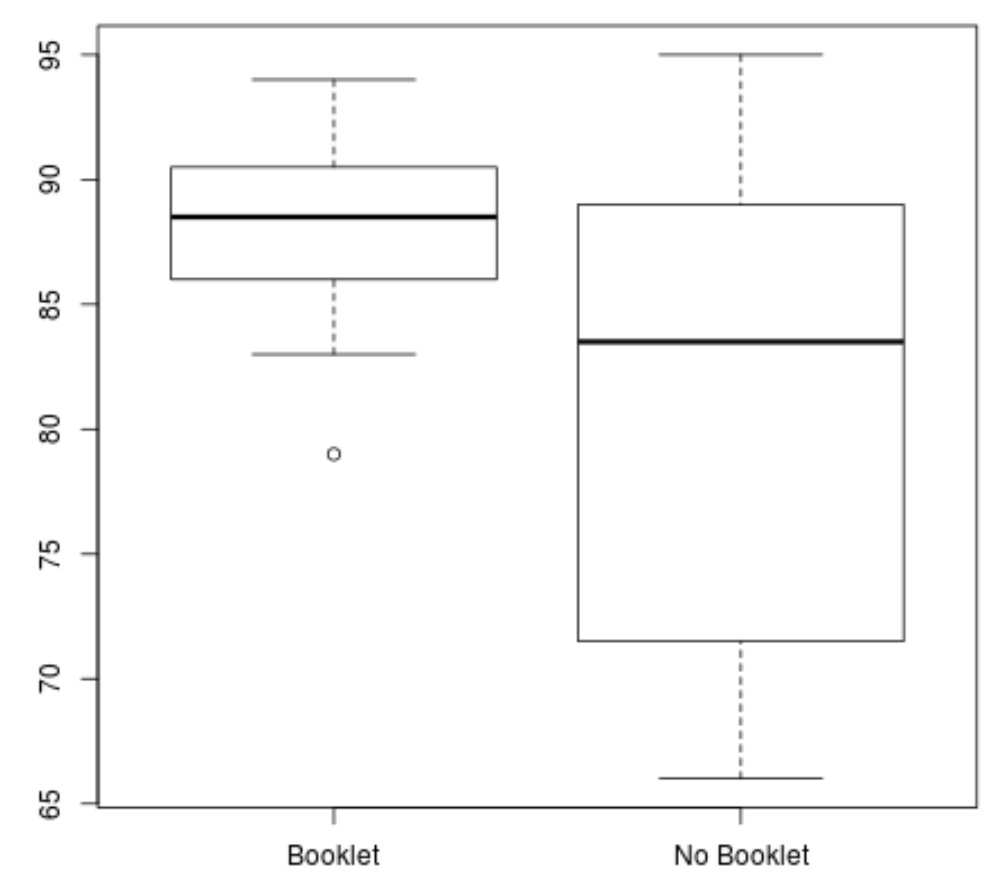
Wyraźnie widać, że grupa „Broszura” ma wyższy średni wynik i mniejszą wariancję ocen.

Aby formalnie sprawdzić, czy średnie wyniki między grupami różnią się istotnie, możemy wykonać test t Welcha:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

Z wyniku widzimy, że statystyka testu t wynosi 2,2361 , a odpowiadająca jej wartość p wynosi 0,04171 .

Ponieważ ta wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową i stwierdzić, że istnieje statystycznie istotna różnica w średnich wynikach egzaminów pomiędzy obiema grupami.

Funkcja t.test() dostarcza nam również następujących informacji:

• 95% przedział ufności dla różnicy średnich wyników egzaminów pomiędzy obiema grupami wynosi [0,3048; 13,8618 ].
• Średni wynik egzaminu pierwszej grupy to 87,91667 .
• Średni wynik egzaminu drugiej grupy to 80,83333 .

Pełną dokumentację funkcji t.test() znajdziesz tutaj .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w języku R:

Jak wykonać test t dla jednej próby w R
Jak wykonać test t dla dwóch próbek w R
Jak wykonać test t dla sparowanych próbek w R
Jak wykreślić wiele wykresów skrzynkowych na jednym wykresie w R