Co to jest test wielomianowy? (definicja – przykład)

Test wielomianowy służy do określenia, czy zmienna kategoryczna ma rozkład hipotetyczny.

W teście tym wykorzystuje się następujące hipotezy zerowe i alternatywne:

H ₀ : Zmienna kategoryczna ma rozkład hipotetyczny.

H _A : Zmienna kategoryczna nie podlega rozkładowi hipotetycznemu.

Jeśli wartość p testu jest poniżej pewnego poziomu istotności (np. α = 0,05), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że zmienna nie ma hipotetycznego rozkładu.

Test ten stosuje się, gdy zmienna może przyjąć k różnych wyników. Klasycznym przykładem testu wielomianowego jest sytuacja, w której chcemy ustalić, czy określone kości są uczciwe. Kiedy rzucasz kostką, prawdopodobieństwo, że wypadnie na każdą liczbę (od 1 do 6) wynosi 1/6.

Aby sprawdzić, czy kość jest sprawiedliwa, możemy rzucić nią kilka razy i sprawdzić, czy liczba trafień na różnych liczbach znacznie różni się od tego, czego byśmy się spodziewali.

Poniższe przykłady pokazują, jak przeprowadzić test wielomianowy przy użyciu statystycznego języka programowania R.

Przykład 1: Uczciwe kostki

Załóżmy, że chcemy ustalić, czy kość jest sprawiedliwa. Aby to przetestować, uruchamiamy go 30 razy i rejestrujemy częstotliwość każdego wyniku. Poniższa tabela przedstawia wyniki:

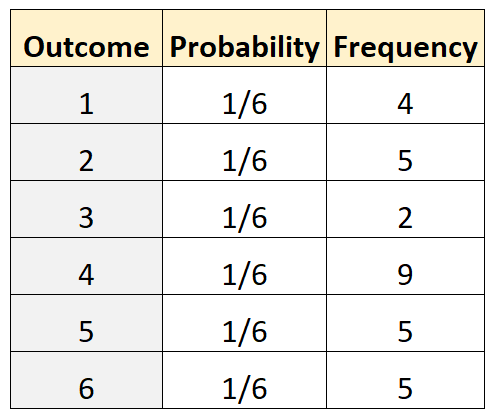
Do przeprowadzenia testu wielomianowego można użyć następującego kodu w języku R:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

Wartość p testu wynosi 0,4306 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie odrzucimy hipotezy zerowej. Nie mamy więc wystarczających dowodów, aby stwierdzić, że kości są niesprawiedliwe.

Przykład 2: Sprzedaż produktu

Załóżmy, że właściciel sklepu stawia hipotezę, że taka sama liczba klientów kupi każdy z czterech różnych produktów. Aby to przetestować, rejestruje liczbę klientów, którzy kupili każdy produkt w danym tygodniu. Poniższa tabela przedstawia wyniki:

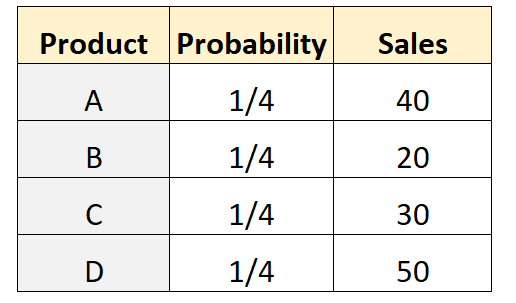
Poniższy kod w języku R może zostać użyty do przeprowadzenia testu wielomianowego na tym zbiorze danych:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

Wartość p testu wynosi 0,00226 . Ponieważ ta wartość p jest mniejsza niż 0,05, odrzucimy hipotezę zerową. Mamy więc wystarczająco dużo dowodów, aby stwierdzić, że sprzedaż nie jest równa dla każdego produktu.

Przykład 3: Kulki w torbie

Tomek stwierdza, że prawdopodobieństwo wybrania z worka czerwonej, zielonej lub fioletowej kulki wynosi odpowiednio 0,2, 0,5 i 0,3. Aby to sprawdzić, jego przyjaciel Mike sięga do torby i wyciąga kulkę (z zamiennikami) 100 razy. Poniższa tabela przedstawia wyniki:

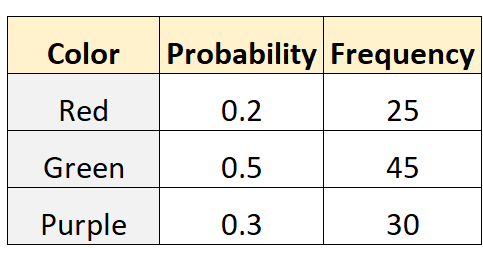
Poniższy kod w języku R może zostać użyty do przeprowadzenia testu wielomianowego na tym zbiorze danych:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

Wartość p testu wynosi 0,3999 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie uda nam się odrzucić hipotezy zerowej. Dlatego nie mamy wystarczających dowodów, aby stwierdzić, że rozmieszczenie kulek w worku różni się od tego określonego przez Toma.

Dodatkowe zasoby

Wprowadzenie do rozkładu wielomianowego
Kalkulator rozkładu wielomianowego