Testowanie hipotez pod kątem wariancji

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, na czym polega testowanie hipotez pod kątem wariancji. Znajdziesz więc wzór na sprawdzenie hipotezy wariancyjnej oraz dodatkowo rozwiązane krok po kroku ćwiczenie.

Na czym polega testowanie hipotez pod kątem wariancji?

Testowanie hipotez pod kątem wariancji to metoda statystyczna stosowana do określenia, czy odrzucić hipotezę zerową dotyczącą wariancji populacji. Innymi słowy, testowanie hipotezy wariancji służy do odrzucenia lub przyjęcia hipotezy o wartości wariancji populacji.

W szczególności, w zależności od wartości statystyki testowej hipotezy dla wariancji i wybranego poziomu istotności, hipoteza zerowa jest odrzucana lub akceptowana.

Należy pamiętać, że testowanie hipotez ma wiele nazw, można je również nazwać kontrastami hipotez, testowaniem hipotez lub testowaniem istotności.

Wzór testowania hipotez na wariancję

Statystyka testu hipotezy dotycząca wariancji jest równa różnicy między liczebnością próby minus jednokrotność wariancji próby i podzieloną przez proponowaną wartość wariancji populacji. Statystyka testu hipotezy dotycząca wariancji ma rozkład chi-kwadrat .

Zatem wzór na obliczenie statystyki testu hipotezy dla wariancji jest następujący:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Złoto:

$\chi^2$

jest statystyką testującą hipotezę dotyczącą wariancji, która ma rozkład chi-kwadrat.
$n$

to wielkość próbki.
$s^2$

jest wariancją próbki.
$\sigma^2$

jest proponowaną wariancją populacji.

Aby zinterpretować wynik statystyki, uzyskaną wartość należy porównać z wartością krytyczną testu.

Jeśli test hipotezy na wariancję jest dwustronny, hipoteza zerowa jest odrzucana, jeśli statystyka jest większa niż wartość krytyczna.
$\chi_{1-\alpha/2|n-1}^2$

lub jeśli wartość krytyczna jest mniejsza niż

$\chi_{\alpha/2|n-1}$

.
Jeśli test hipotezy dla wariancji pasuje do prawego ogona, hipoteza zerowa jest odrzucana, jeśli statystyka jest większa niż wartość krytyczna
$\chi_{1-\alpha|n-1}^2$

.
Jeżeli test hipotezy pod kątem wariancji pasuje do lewego ogona, hipoteza zerowa zostaje odrzucona, jeśli statystyka jest mniejsza niż wartość krytyczna
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Wartości testowe hipotezy krytycznej dla wariancji uzyskuje się z tabeli rozkładu chi-kwadrat. Należy zauważyć, że stopnie swobody rozkładu Chi-kwadrat to wielkość próby minus 1.

Przykład sprawdzania hipotez w świecie rzeczywistym pod kątem wariancji

Po zapoznaniu się z definicją testowania hipotezy wariancji i jej wzorem, zobaczymy konkretny przykład, który zakończy przyswajanie tej koncepcji.

W fabryce znajduje się maszyna, która z dużą precyzją produkuje części do samochodu. Podejrzewa się jednak, że odeszła i obecnie produkuje części ze szczeliną większą niż 8 mm ² . Aby obalić tę hipotezę, analizuje się próbkę składającą się z 25 sztuk, a jej wariancja próbki wynosi 9,1 mm ² . Czy hipotezę wyjściową można odrzucić przy poziomie istotności α=0,05?

Hipoteza zerowa i hipoteza alternatywna dla tego testu hipotezy wariancji są następujące:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Aby określić, czy hipotezę zerową można odrzucić, obliczamy statystykę testu hipotezy dla wariancji, korzystając ze wzoru, który widzieliśmy powyżej: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Teraz szukamy wartości krytycznej odpowiadającej prawemu ogonowi dla 24 stopni swobody i poziomu istotności α=0,05 w tabeli rozkładu Chi-kwadrat:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Zatem obliczona statystyka jest mniejsza niż wartość krytyczna testu, w związku z czym hipoteza zerowa testu hipotezy wariancji nie jest odrzucana, lecz odrzucana jest hipoteza alternatywna.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Zobacz: Testowanie hipotez dla średniej populacji
➤ Zobacz: Testowanie hipotez dotyczących proporcji populacji

Testowanie hipotez dla wariancji dwóch populacji

Testowanie hipotezy wariancji w dwóch populacjach służy do odrzucenia lub przyjęcia hipotezy, że wariancje dwóch różnych populacji są równe.

Zatem hipoteza zerowa testu hipotezy dotyczącej wariancji dwóch populacji jest zawsze następująca:

$H_0: \sigma^2_1=\sigma^2_2$

Hipotezą alternatywną może być jedna z trzech opcji:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

W tym przypadku wzór na obliczenie statystyki testu hipotezy dla wariancji dwóch populacji jest następujący:

$F=\cfrac{s_1^2}{s_2^2}$

Złoto:

$F$

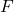
jest statystyką testującą hipotezę dotyczącą wariancji dwóch populacji, która jest zgodna z rozkładem F .
$\sigma_1^2$

jest wariancją populacji 1.
$\sigma_2^2$

jest wariancją populacji 2.
$s_1^2$

jest wariancją próbki 1.
$s_2^2$

jest wariancją próbki 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Ponieważ rozkład Snedecora F nie jest symetryczny, hipotezę zerową odrzuca się w oparciu o następujące kryteria:

[lateks]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{czarny} \ \text{If }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej