Test u manna – whitneya
Test U Manna-Whitneya (czasami nazywany testem sumy rang Wilcoxona) służy do porównywania różnic między dwiema niezależnymi próbkami, gdy rozkłady próbek nie mają rozkładu normalnego, a liczebność próbek jest mała (n < 30).
Uważa się, że jest to nieparametryczny odpowiednik niezależnego testu t dla dwóch próbek .
Oto kilka przykładów, kiedy można zastosować test U Manna-Whitneya:
- Chcesz porównać wynagrodzenia pięciu absolwentów uniwersytetu A z wynagrodzeniami pięciu absolwentów uniwersytetu B. Wynagrodzenia nie podlegają rozkładowi normalnemu.
- Chcesz wiedzieć, czy utrata masy ciała różni się w przypadku dwóch grup: 12 osób stosujących dietę A i 10 osób stosujących dietę B. Utrata masy ciała nie ma rozkładu normalnego.
- Chcesz wiedzieć, czy wyniki 8 uczniów w klasie A różnią się od wyników 7 uczniów w klasie B. Wyniki nie mają rozkładu normalnego.
W każdym przykładzie chcesz porównać dwie grupy, rozkład próbkowania nie jest normalny, a liczebność próby jest mała.
Zatem test U Manna-Whitneya jest odpowiedni, o ile spełnione są następujące założenia.
Założenia testu U Manna-Whitneya
Przed wykonaniem testu U Manna-Whitneya należy upewnić się, że spełnione są następujące cztery założenia:
- Zwykła lub ciągła: Zmienna, którą analizujesz, jest porządkowa lub ciągła. Przykładami zmiennych porządkowych są pozycje Likerta (np. 5-punktowa skala od „zdecydowanie się nie zgadzam” do „zdecydowanie się zgadzam”). Przykładami zmiennych ciągłych są wzrost (mierzony w calach), waga (mierzona w funtach) lub wyniki testów (mierzone od 0 do 100).
- Niezależność: Wszystkie obserwacje z obu grup są od siebie niezależne.
- Kształt: Kształty rozkładów dla obu grup są w przybliżeniu takie same.
Jeśli te założenia są spełnione, można wykonać test U Manna-Whitneya.
Jak wykonać test U Manna-Whitneya
Aby wykonać test U Manna-Whitneya, postępujemy zgodnie ze standardową pięcioetapową procedurą testowania hipotez :
1. Podaj założenia.
W większości przypadków test U Manna-Whitneya wykonywany jest jako test dwustronny. Hipotezy zerowe i alternatywne zapisuje się w postaci:
H 0 : Obie populacje są równe
H a : Te dwie populacje nie są równe
2. Określ poziom istotności, jaki należy zastosować w przypadku hipotezy.
Zdecyduj się na poziom istotności. Typowe wybory to .01, .05 i .1.
3. Znajdź statystykę testową.
Statystyka testowa jest oznaczona jako U i jest mniejszą z wartości U 1 i U 2 , jak zdefiniowano poniżej:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
gdzie n 1 i n 2 to wielkości próbek odpowiednio dla próbek 1 i 2, a R 1 i R 2 to suma rang odpowiednio dla próbek 1 i 2.
Poniższe przykłady pokażą, jak szczegółowo znaleźć tę statystykę testową.
4. Odrzuć lub nie odrzucaj hipotezy zerowej.
Korzystając ze statystyk testowych, określ, czy możesz odrzucić hipotezę zerową, na podstawie poziomu istotności i wartości krytycznej podanych w tabeli U Manna-Whitneya.
5. Interpretacja wyników.
Interpretuj wyniki testu w kontekście zadanego pytania.
Przykłady wykonania testu U Manna-Whitneya
Poniższe przykłady pokazują, jak przeprowadzić test U Manna-Whitneya.
Przykład 1
Chcemy wiedzieć, czy nowy lek skutecznie zapobiega atakom paniki. Łącznie 12 pacjentów podzielono losowo na dwie grupy po 6 osób i przydzielono do grupy otrzymującej nowy lek lub placebo. Następnie pacjenci rejestrują liczbę ataków paniki, których doświadczyli w ciągu miesiąca.
Wyniki przedstawiono poniżej:
| NOWY LEK | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Wykonaj test U Manna-Whitneya, aby sprawdzić, czy istnieje różnica w liczbie ataków paniki wśród pacjentów w grupie placebo w porównaniu z grupą nowego leku. Użyj poziomu istotności 0,05.
1. Podaj założenia.
H 0 : Obie populacje są równe
H a : Te dwie populacje nie są równe
2. Określ poziom istotności, jaki należy zastosować w przypadku hipotezy.
Problem mówi nam, że powinniśmy zastosować poziom istotności 0,05.
3. Znajdź statystykę testową.
Przypomnijmy, że statystyka testowa jest oznaczona jako U i jest mniejszą z wartości U 1 i U 2 , jak zdefiniowano poniżej:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
gdzie n 1 i n 2 to wielkości próbek odpowiednio dla próbek 1 i 2, a R 1 i R 2 to suma rang odpowiednio dla próbek 1 i 2.
Aby znaleźć R 1 i R 2 , musimy połączyć obserwacje z obu grup i uporządkować je od najmniejszej do największej:
| NOWY LEK | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Całkowita próbka: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Rangi: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = suma rang dla próby 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = suma rang dla próby 2 = 1,5+3+6,5+10+11+12 = 44
Następnie używamy wielkości próbek n 1 i n 2 , a także sumy rang R 1 i R 2 , aby znaleźć U 1 i U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Nasze statystyki testowe to mniejsza z wartości U1 i U2 , która wynosi U=13.
Uwaga: Możemy również użyć kalkulatora testu U Manna-Whitneya, aby ustalić, że U = 13.
4. Odrzuć lub nie odrzucaj hipotezy zerowej.
Stosując n 1 = 6 i n 2 = 6 z poziomem istotności 0,05, tabela U Manna-Whitneya mówi nam, że wartość krytyczna wynosi 5:
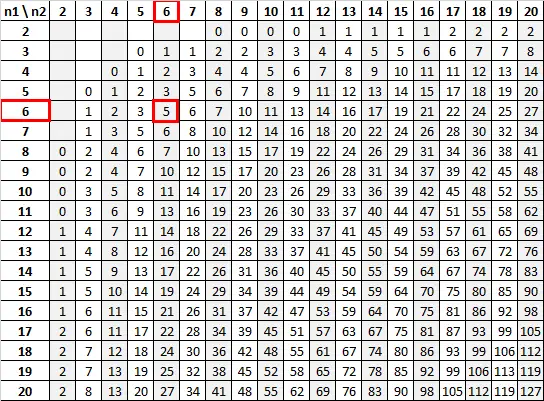
Ponieważ nasza statystyka testowa (13) jest większa niż wartość krytyczna (5), nie możemy odrzucić hipotezy zerowej.
5. Interpretacja wyników.
Ponieważ nie odrzuciliśmy hipotezy zerowej, nie mamy wystarczających dowodów, aby stwierdzić, że liczba ataków paniki doświadczanych przez pacjentów w grupie placebo różni się od tej w grupie nowego leku.
Przykład 2
Chcemy wiedzieć, czy nauka przez 30 minut dziennie przez tydzień pomaga uczniom osiągać lepsze wyniki na teście. Łącznie 15 pacjentów przydzielono losowo do grupy badanej lub do żadnej grupy badawczej. Po tygodniu wszyscy uczniowie przystępują do tego samego testu.
Wyniki testów dla obu grup przedstawiono poniżej:
| BADANIE | BEZ STUDIÓW |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Wykonaj test U Manna-Whitneya, aby sprawdzić, czy istnieje różnica w wynikach testu dla grupy badanej w porównaniu z grupą niebadaną. Użyj poziomu istotności 0,01.
1. Podaj założenia.
H 0 : Obie populacje są równe
H a : Te dwie populacje nie są równe
2. Określ poziom istotności, jaki należy zastosować w przypadku hipotezy.
Problem mówi nam, że powinniśmy zastosować poziom istotności 0,01.
3. Znajdź statystykę testową.
Przypomnijmy, że statystyka testowa jest oznaczona jako U i jest mniejszą z wartości U 1 i U 2 , jak zdefiniowano poniżej:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
gdzie n 1 i n 2 to wielkości próbek odpowiednio dla próbek 1 i 2, a R 1 i R 2 to suma rang odpowiednio dla próbek 1 i 2.
Aby znaleźć R 1 i R 2 , musimy połączyć obserwacje z obu grup i uporządkować je od najmniejszej do największej:
| BADANIE | BEZ STUDIÓW |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Całkowita próbka: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Rzędy: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = suma rang dla próby 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = suma rang dla próby 2 = 1+2+3+4+6+11+13 = 40
Następnie używamy wielkości próbek n 1 i n 2 , a także sumy rang R 1 i R 2 , aby znaleźć U 1 i U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Nasze statystyki testowe to mniejsza z wartości U1 i U2 , która wynosi U=12.
Uwaga: Możemy również użyć kalkulatora testu U Manna-Whitneya, aby ustalić, że U = 12.
4. Odrzuć lub nie odrzucaj hipotezy zerowej.
Stosując n 1 = 8 i n 2 = 7 z poziomem istotności 0,01, tabela U Manna-Whitneya mówi nam, że wartość krytyczna wynosi 6:
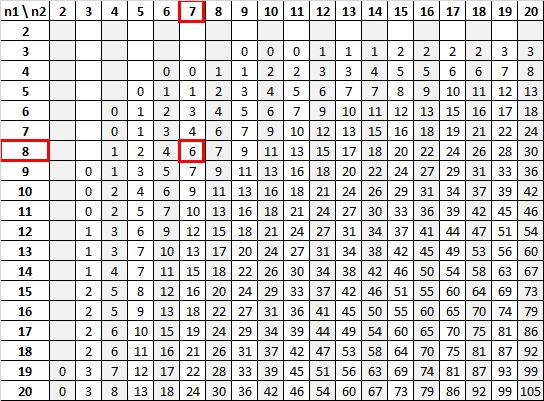
Ponieważ nasza statystyka testowa (12) jest większa niż wartość krytyczna (6), nie możemy odrzucić hipotezy zerowej.
5. Interpretacja wyników.
Ponieważ nie odrzuciliśmy hipotezy zerowej, nie mamy wystarczających dowodów, aby stwierdzić, że wyniki uczniów, którzy studiowali, na testach różnią się od wyników uczniów, którzy się nie uczyli.
Dodatkowe zasoby
Kalkulator testu U Manna-Whitneya
Stół Manna-Whitneya U
Jak wykonać test U Manna-Whitneya w programie Excel
Jak wykonać test U Manna-Whitneya w R
Jak wykonać test U Manna-Whitneya w Pythonie
Jak wykonać test U Manna-Whitneya w SPSS
Jak wykonać test U Manna-Whitneya w Stata
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej