Jak obliczyć współczynnik inflacji wariancji (vif) w sas

W analizie regresji wieloliniowość występuje, gdy dwie lub więcej zmiennych predykcyjnych jest ze sobą silnie skorelowanych, tak że nie dostarczają unikalnych lub niezależnych informacji w modelu regresji.

Jeśli stopień korelacji między zmiennymi jest wystarczająco wysoki, może to powodować problemy podczas dopasowywania i interpretacji modelu regresji.

Jednym ze sposobów wykrycia współliniowości jest użycie metryki zwanej współczynnikiem inflacji wariancji (VIF) , która mierzy korelację i siłę korelacji między zmiennymi objaśniającymi w modelu regresji .

W tym samouczku wyjaśniono, jak obliczyć VIF w SAS-ie.

Przykład: obliczanie VIF w SAS

Na potrzeby tego przykładu utworzymy zbiór danych opisujący atrybuty 10 koszykarzy:

 /*create dataset*/
data my_data;
    input rating points assists rebounds;
    datalines ;
90 25 5 11
85 20 7 8
82 14 7 10
88 16 8 6
94 27 5 6
90 20 7 9
76 12 6 6
75 15 9 10
87 14 9 10
86 19 5 7
;
run ;

/*view dataset*/
proc print data =my_data; 

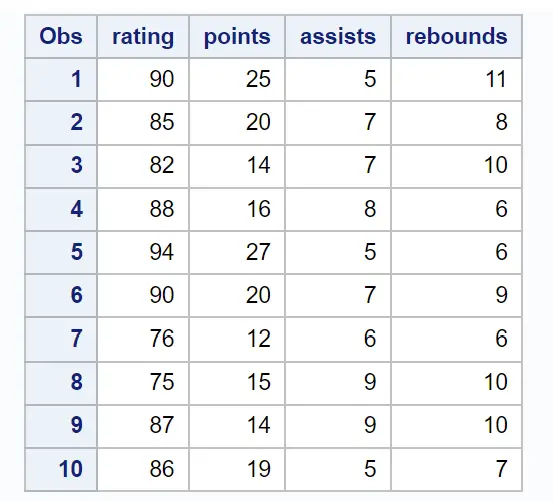
Załóżmy, że chcemy dopasować model regresji liniowej, wykorzystując punktację jako zmienną odpowiedzi oraz punkty , asysty i zbiórki jako zmienne predykcyjne.

Możemy użyć PROC REG , aby dopasować ten model regresji z opcją VIF do obliczenia wartości VIF dla każdej zmiennej predykcyjnej w modelu:

 /*fit regression model and calculate VIF values*/
proc reg data =my_data;
    model rating = points assists rebounds / lively ;
run ; 

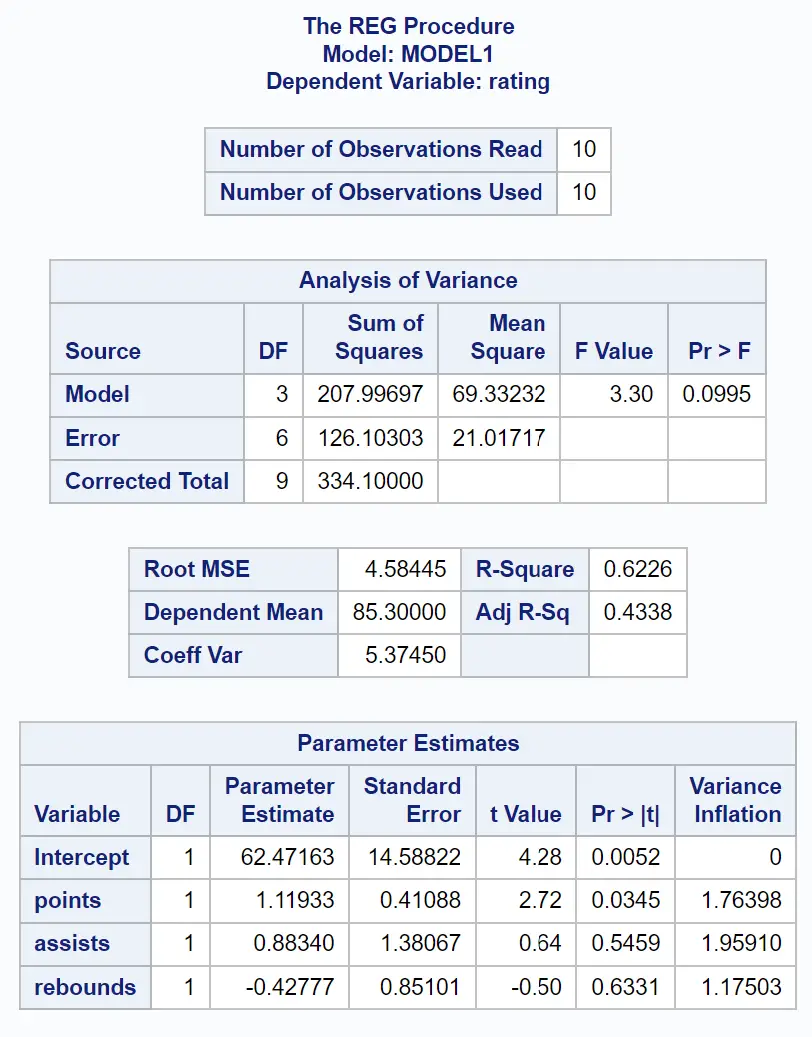
Z tabeli Oszacowania parametrów możemy zobaczyć wartości VIF dla każdej ze zmiennych predykcyjnych:

• punktów: 1,76398
• asysty: 1,96591
• zbiórki: 1,17503

Uwaga: Zignoruj VIF dla „Przechwytywania” w szablonie, ponieważ ta wartość nie jest istotna.

Wartość VIF zaczyna się od 1 i nie ma górnej granicy. Ogólna zasada interpretacji VIF jest następująca:

• Wartość 1 wskazuje, że nie ma korelacji pomiędzy daną zmienną predykcyjną a jakąkolwiek inną zmienną predykcyjną w modelu.
• Wartość od 1 do 5 wskazuje na umiarkowaną korelację między daną zmienną predykcyjną a innymi zmiennymi predykcyjnymi w modelu, ale często nie jest ona na tyle poważna, aby wymagała szczególnej uwagi.
• Wartość większa niż 5 wskazuje na potencjalnie poważną korelację pomiędzy daną zmienną predykcyjną a innymi zmiennymi predykcyjnymi w modelu. W tym przypadku szacunki współczynników i wartości p w wynikach regresji są prawdopodobnie niewiarygodne.

Ponieważ każda z wartości VIF zmiennych predykcyjnych w naszym modelu regresji jest bliska 1, w naszym przykładzie wieloliniowość nie stanowi problemu.

Jak sobie radzić z wielowspółliniowością

Jeśli stwierdzisz, że współliniowość jest problemem w Twoim modelu regresji, istnieje kilka typowych sposobów jego rozwiązania:

1. Usuń jedną lub więcej wysoce skorelowanych zmiennych.

W większości przypadków jest to najszybsze rozwiązanie i często akceptowalne, ponieważ usuwane zmienne i tak są zbędne i dodają niewiele unikalnych lub niezależnych informacji do modelu.

2. Liniowo łączy w jakiś sposób zmienne predykcyjne, na przykład dodając je lub odejmując.

W ten sposób można utworzyć nową zmienną obejmującą informacje z obu zmiennych i nie będzie już występował problem współliniowości.

3. Wykonaj analizę zaprojektowaną w celu uwzględnienia silnie skorelowanych zmiennych, taką jak analiza głównych składowych lub regresja metodą cząstkowych najmniejszych kwadratów (PLS).

Techniki te są specjalnie zaprojektowane do obsługi wysoce skorelowanych zmiennych predykcyjnych.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak wykonać wielokrotną regresję liniową w SAS-ie
Jak utworzyć wykres resztkowy w SAS-ie
Jak obliczyć odległość gotowania w SAS