Jak wykonać transformację boxa-coxa w r (z przykładami)

Transformacja Boxa-Coxa jest powszechnie stosowaną metodą przekształcania zbioru danych o rozkładzie normalnym w zbiór o bardziej normalnym rozkładzie.

Podstawową ideą tej metody jest znalezienie takiej wartości λ, aby przekształcone dane były jak najbardziej zbliżone do rozkładu normalnego, korzystając ze wzoru:

• y(λ) = (y ^λ – 1) / λ jeśli y ≠ 0
• y(λ) = log(y), jeśli y = 0

Możemy wykonać transformację box-cox w R za pomocą funkcji boxcox() z biblioteki MASS() . Poniższy przykład pokazuje, jak w praktyce wykorzystać tę funkcję.

Zapoznaj się z tym artykułem z Uniwersytetu Connecticut, aby uzyskać ładne podsumowanie rozwoju transformacji Boxa-Coxa.

Przykład: Transformacja Boxa-Coxa w R

Poniższy kod pokazuje, jak dopasować model regresji liniowej do zbioru danych, a następnie użyć funkcji boxcox() , aby znaleźć optymalną lambdę do przekształcenia zmiennej odpowiedzi i dopasowania do nowego modelu.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

Optymalna lambda okazała się -0,4242424 . Tym samym w nowym modelu regresji pierwotną zmienną odpowiedzi y zastąpiono zmienną y = (y ^-0,4242424 – 1) / -0,4242424.

Poniższy kod pokazuje, jak utworzyć dwa wykresy QQ w języku R, aby zwizualizować różnice w resztach między dwoma modelami regresji:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

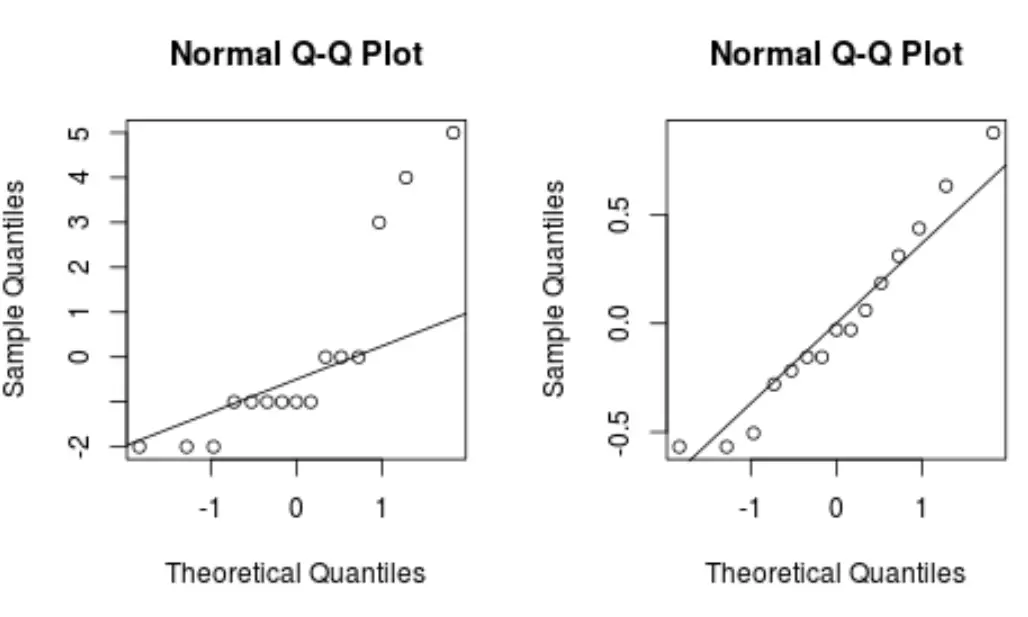
Ogólnie rzecz biorąc, jeśli punkty danych leżą wzdłuż prostej linii ukośnej na wykresie QQ, zbiór danych prawdopodobnie ma rozkład normalny.

Zwróć uwagę, jak model przekształcony przez Boxa-Coxa tworzy wykres QQ o znacznie prostszej linii niż oryginalny model regresji.

Wskazuje to, że reszty modelu przekształconego Box-Coxa mają znacznie bardziej normalny rozkład, co spełnia jedno z założeń regresji liniowej .

Dodatkowe zasoby

Jak przekształcać dane w R (log, pierwiastek kwadratowy, pierwiastek sześcienny)
Jak utworzyć i zinterpretować wykres QQ w R
Jak wykonać test Shapiro-Wilka na normalność w R