Moda (statystyki)
W tym artykule wyjaśniono, jaki tryb znajduje się w statystykach. Dowiesz się, jak znaleźć tryb statystyczny dla danych zgrupowanych i niezgrupowanych, różne typy trybów i kilka przykładów tej miary statystycznej.
Co to jest tryb w statystykach?
W statystyce tryb to wartość w zbiorze danych, która ma najwyższą częstotliwość bezwzględną, to znaczy tryb jest najczęściej powtarzaną wartością w zbiorze danych.
Dlatego, aby obliczyć modę zbioru danych statystycznych, wystarczy policzyć, ile razy każdy element danych pojawia się w próbce, a modą będą najczęściej powtarzające się dane.
Tryb służy do definiowania rozkładu statystycznego, ponieważ najczęściej powtarzająca się wartość znajduje się zwykle w środku rozkładu.
Tryb można również nazwać trybem statystycznym lub wartością modalną . Podobnie, gdy dane są pogrupowane w interwały, najczęściej powtarzającym się interwałem jest interwał modalny lub klasa modalna .
Ogólnie termin Mo jest używany jako symbol trybu statystycznego, na przykład tryb rozkładu X to Mo(X).
Należy pamiętać, że tryb jest statystyczną miarą położenia centralnego, a także medianą i średnią. Poniżej zobaczymy, co oznacza każda z tych miar statystycznych.
Typy trybów w statystykach
W statystyce istnieje kilka rodzajów trybów, które są klasyfikowane według liczby najczęściej powtarzanych wartości:
- Tryb unimodalny : istnieje tylko jedna wartość z maksymalną liczbą powtórzeń. Na przykład [1, 4, 2, 4, 5, 3].
- Tryb bimodalny : Maksymalna liczba powtórzeń występuje przy dwóch różnych wartościach, a obie wartości powtarzane są taką samą liczbę razy. Na przykład [2, 6, 7, 2, 3, 6, 9].
- Tryb multimodalny : Trzy lub więcej wartości mają tę samą maksymalną liczbę powtórzeń. Na przykład [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
Jak znaleźć tryb statystyczny
Aby znaleźć tryb statystyczny zbioru danych, należy wykonać następujące kroki:
- Uporządkuj dane. Ten krok nie jest obowiązkowy, ale ułatwi liczenie liczb.
- Policz, ile razy pojawia się każda liczba.
- Liczba, która pojawia się najczęściej, to tryb statystyczny.
Przykłady trybu statystycznego
Biorąc pod uwagę definicję mody w statystykach, poniżej możesz zobaczyć przykład każdego rodzaju mody, abyś mógł lepiej zrozumieć to pojęcie.
Przykład trybu unimodalnego
- Jaki jest tryb następującego zbioru danych?
![]()
Numery nie są uporządkowane, dlatego uporządkujemy je w pierwszej kolejności, aby ułatwić znalezienie trybu.
![]()
Cyfry 2 i 9 pojawiają się dwukrotnie, natomiast cyfra 5 powtarza się trzykrotnie. Dlatego mod serii danych ma numer 5.
![]()
Przykład trybu bimodalnego
- Oblicz modę następującego zbioru danych:
![]()
![]()
Najpierw porządkujemy liczby:
![]()
![]()
Jak widać, cyfra 6 i cyfra 8 pojawiają się w sumie cztery razy, czyli jest to maksymalna liczba powtórzeń. Dlatego w tym przypadku jest to tryb bimodalny, a dwie liczby oznaczają tryb zbioru danych:
![]()
Przykład trybu multimodalnego
- Znajdź następujący tryb zbioru danych:
![]()
![]()
![]()
Ponieważ danych jest dużo, najpierw sortujemy je w kolejności rosnącej, aby ułatwić policzenie:
![]()
![]()
![]()
Najczęściej powtarzającymi się liczbami są 20, 27 i 31, wszystkie trzy liczby powtarzają się pięć razy. Tryb tego przykładu jest zatem multimodalny.
![]()
kalkulator mody
Wprowadź dane z dowolnej próbki statystycznej do poniższego kalkulatora online, aby obliczyć jej tryb. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Tryb dla danych grupowanych
Kiedy mamy dane pogrupowane w formie interwałów, tak naprawdę nie wiemy, ile razy każdy fragment danych jest powtarzany, znamy jedynie częstotliwość każdego interwału.
Aby więc obliczyć modę danych pogrupowanych w przedziały, musimy skorzystać ze wzoru :
![]()
Złoto:
- L i jest dolną granicą przedziału modalnego (najwyższy bezwzględny przedział częstotliwości).
- f i jest częstotliwością bezwzględną przedziału modowego.
- f i-1 jest częstotliwością bezwzględną przedziału przed modalem.
- f i+1 jest częstotliwością bezwzględną przedziału po modalu.
- A i jest szerokością przedziału modalnego.
Dla przykładu, poniżej rozwiązałeś ćwiczenie, w którym obliczany jest tryb danych pogrupowanych w przedziały:
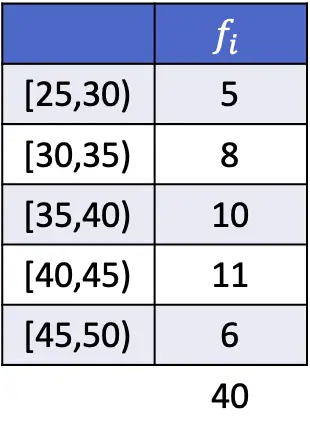
W tym przypadku przedział modalny wynosi [40,45), ponieważ jest to przedział o największej częstotliwości bezwzględnej. Dlatego parametry formuły trybu dla zgrupowanych danych to:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
Stosujemy zatem wzór na określenie postaci danych pogrupowanych w przedziały i wykonujemy obliczenia:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
Różnica między modą, średnią i medianą
W tej ostatniej sekcji zobaczymy, jaka jest różnica między modą, średnią i medianą. Ponieważ wszystkie trzy są statystycznymi miarami pozycji centralnej, ich znaczenie jest inne.
Jak wyjaśniono w całym artykule, mod w matematyce jest najczęściej powtarzającą się wartością w zbiorze danych.
Po drugie, średnia jest średnią wartością wszystkich danych statystycznych. Zatem, aby uzyskać średnią z określonych danych, należy dodać wszystkie dane, a następnie podzielić wynik przez liczbę obserwacji.
I wreszcie mediana to wartość, która zajmuje centralną pozycję podczas porządkowania danych.
Zatem trzy miary statystyczne pomagają zdefiniować rozkład prawdopodobieństwa, ponieważ dają wyobrażenie o jego wartościach centralnych. Należy jednak pamiętać, że nie ma jednej miary, która byłaby lepsza od drugiej, oznaczają one po prostu różne koncepcje.
Właściwości mody
Właściwości mody to:
- Tryb można znaleźć zarówno w zmiennych ilościowych, jak i zmiennych jakościowych.
- Jeśli zastosujemy transformację liniową do zmiennej losowej, wartość średniej będzie się zmieniać w zależności od zastosowanych operacji.
- Ogólnie rzecz biorąc, tryb jest niewrażliwy na wartości odstające.
- Jeśli wszystkie wartości mają tę samą częstotliwość, nie ma trybu.
![]()