Problem trzeciej zmiennej: definicja i przykład
W statystyce problem trzeciej zmiennej pojawia się, gdy zaobserwowaną korelację między dwiema zmiennymi można w rzeczywistości wyjaśnić trzecią zmienną, która nie została wzięta pod uwagę.
Jeżeli ta trzecia zmienna nie zostanie wzięta pod uwagę, korelacja między dwiema badanymi zmiennymi może wprowadzać w błąd lub nawet prowadzić do nieporozumień.
W tym samouczku przedstawiono kilka przykładów problemów z trzecią zmienną w różnych kontekstach.
Przykład 1: Psy i hydranty przeciwpożarowe
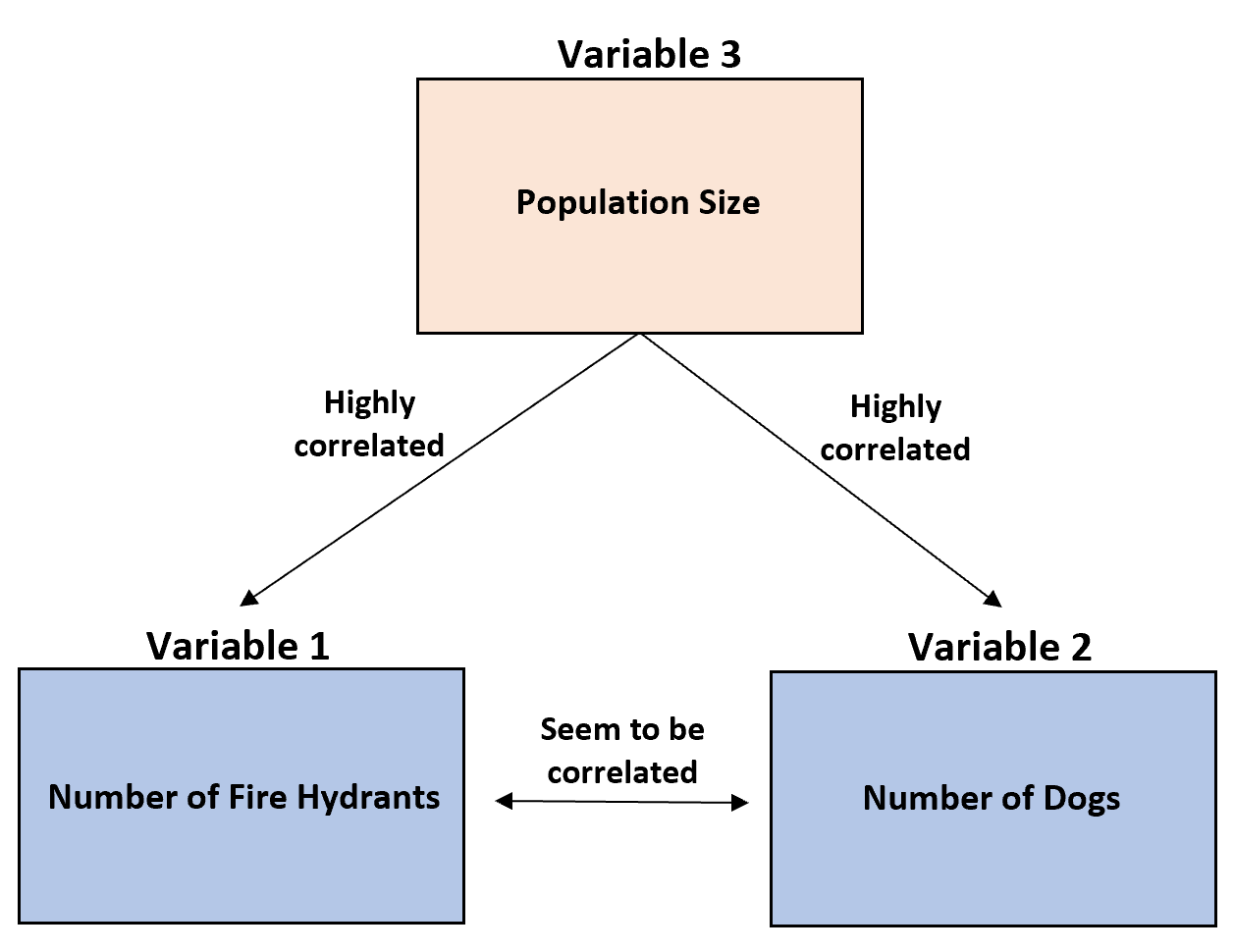
Jeden z badaczy zauważa, że w miastach z większą liczbą hydrantów przeciwpożarowych jest też więcej psów.
Jednakże te dwie zmienne są skorelowane tylko dlatego, że obie mają silną korelację z trzecią zmienną: wielkością populacji .
W większych miastach jest zwykle więcej hydrantów i psów. Z drugiej strony w mniejszych miastach jest zwykle mniej hydrantów i psów.
Przykład 2: Sprzedaż lodów i ataki rekinów
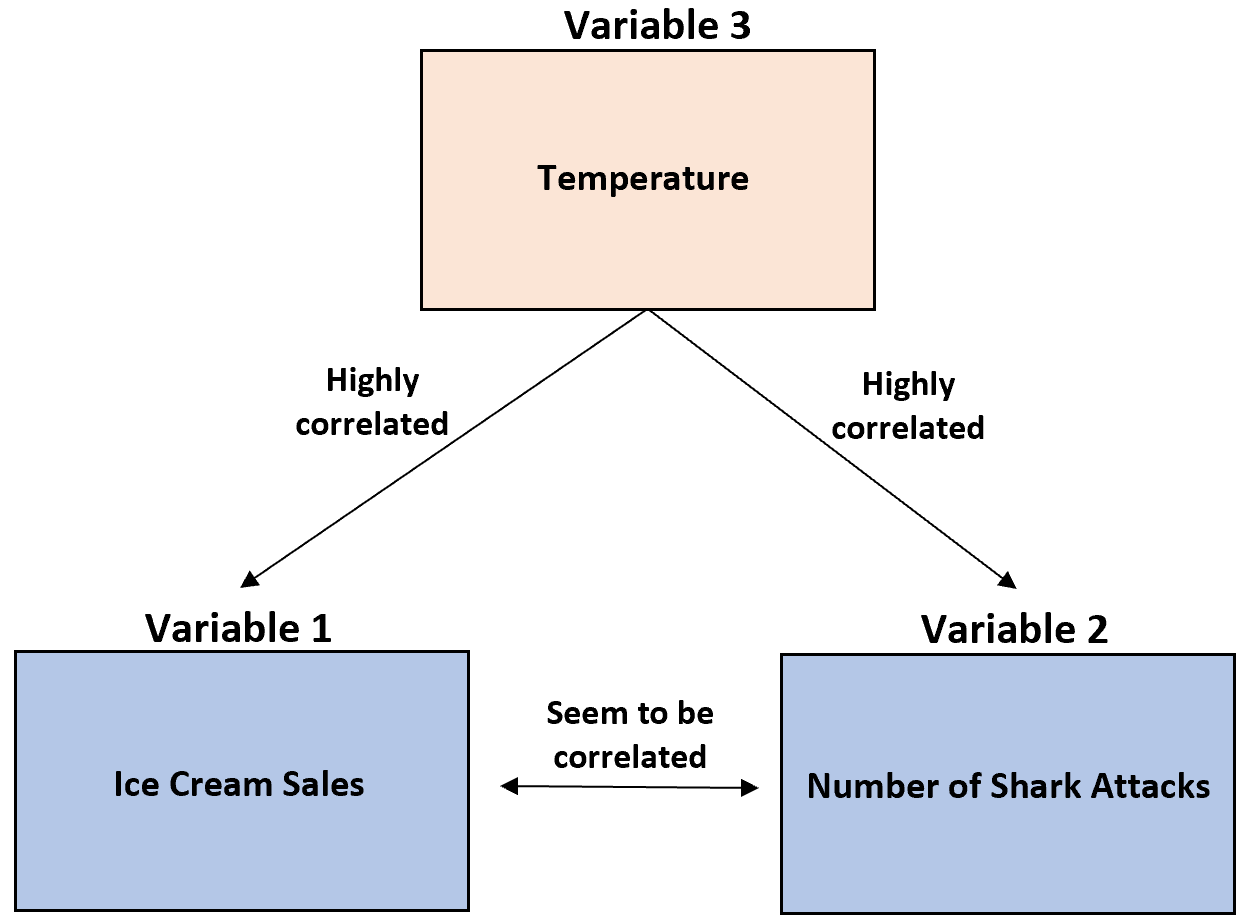
Badacz odkrył, że sprzedaż lodów i ataki rekinów są silnie skorelowane.
Jednakże te dwie zmienne są ze sobą skorelowane tylko dlatego, że obie mają silną korelację z trzecią zmienną: temperaturą .
Kiedy jest cieplej, więcej ludzi kupuje lody i więcej osób kąpie się w oceanie, co wyjaśnia, dlaczego wartość sprzedaży lodów i ataków rekinów zwykle rośnie w tych samych porach roku.
Przykład 3: Wolontariusze i klęski żywiołowe
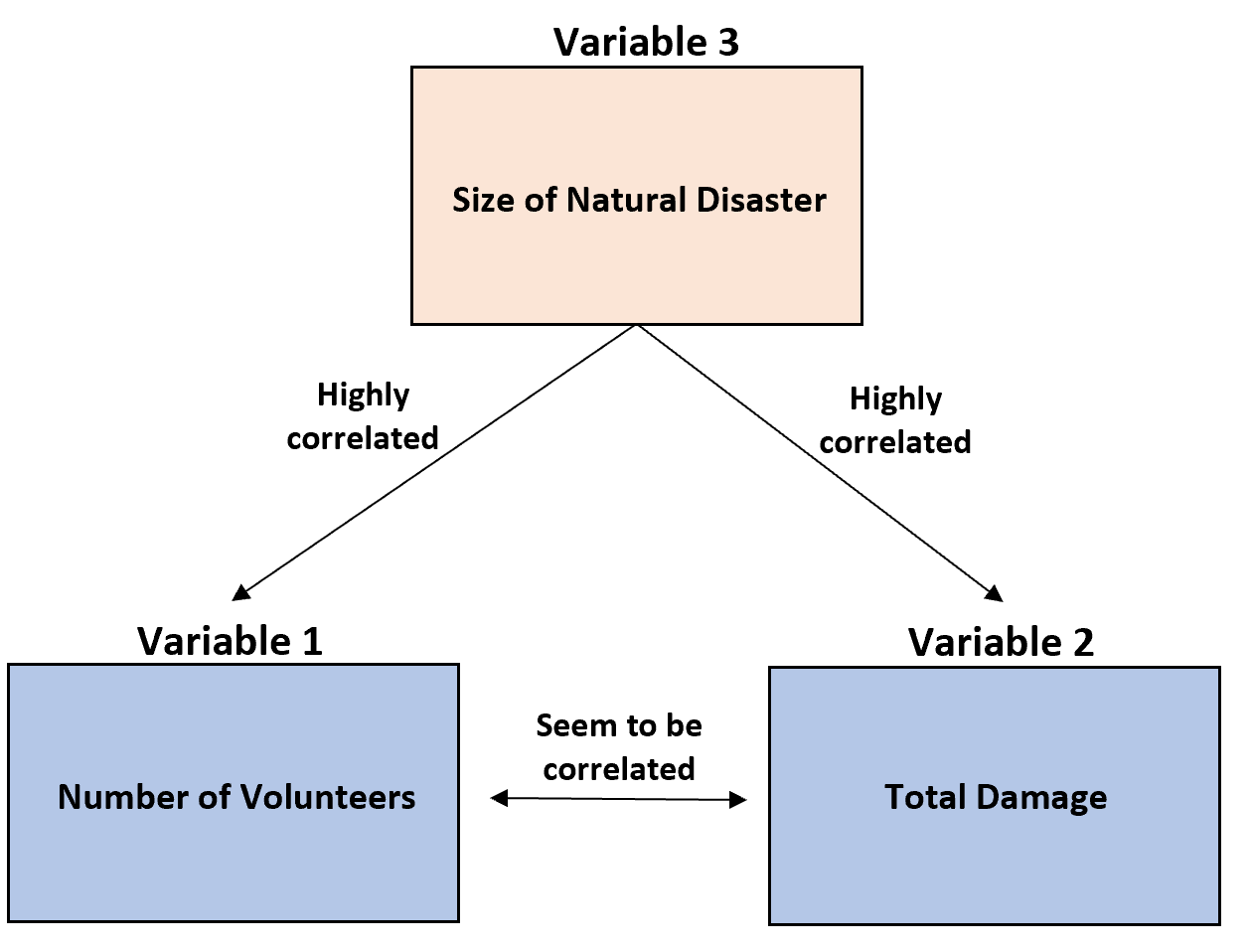
Z badania wynika, że im więcej ochotników zgłasza się po klęsce żywiołowej, tym większe są szkody.
Jednakże te dwie zmienne są ze sobą skorelowane tylko dlatego, że obie mają silną korelację z trzecią zmienną: wielkością klęski żywiołowej .
Większe klęski żywiołowe są silnie powiązane z większą liczbą wyrządzonych szkód i wzrostem liczby wolontariuszy.
Powiązane artykuły
Co to jest pominięte zmienne obciążenie?
Co to jest stronniczość zaniżenia?
Co to jest błąd agregacji?
Co to jest myląca zmienna?