Jak wykonać test post hoc tukeya-kramera w programie excel

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Założenia stosowane w ANOVA są następujące:

Hipoteza zerowa (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (średnie są równe dla każdej grupy)

Hipoteza alternatywna: (Ha): przynajmniej jeden ze środków różni się od pozostałych

Jeżeli wartość p analizy ANOVA jest poniżej poziomu istotności, możemy odrzucić hipotezę zerową i stwierdzić, że mamy wystarczające dowody, aby stwierdzić, że przynajmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe. Aby dokładnie wiedzieć, które grupy się od siebie różnią, należy przeprowadzić test post hoc.

Najczęściej stosowanym testem post hoc jest test Tukeya-Kramera , który porównuje średnią pomiędzy każdą kombinacją parami grup.

Poniższy przykład pokazuje, jak wykonać test Tukeya-Kramera w programie Excel.

Przykład: test Tukeya-Kramera w Excelu

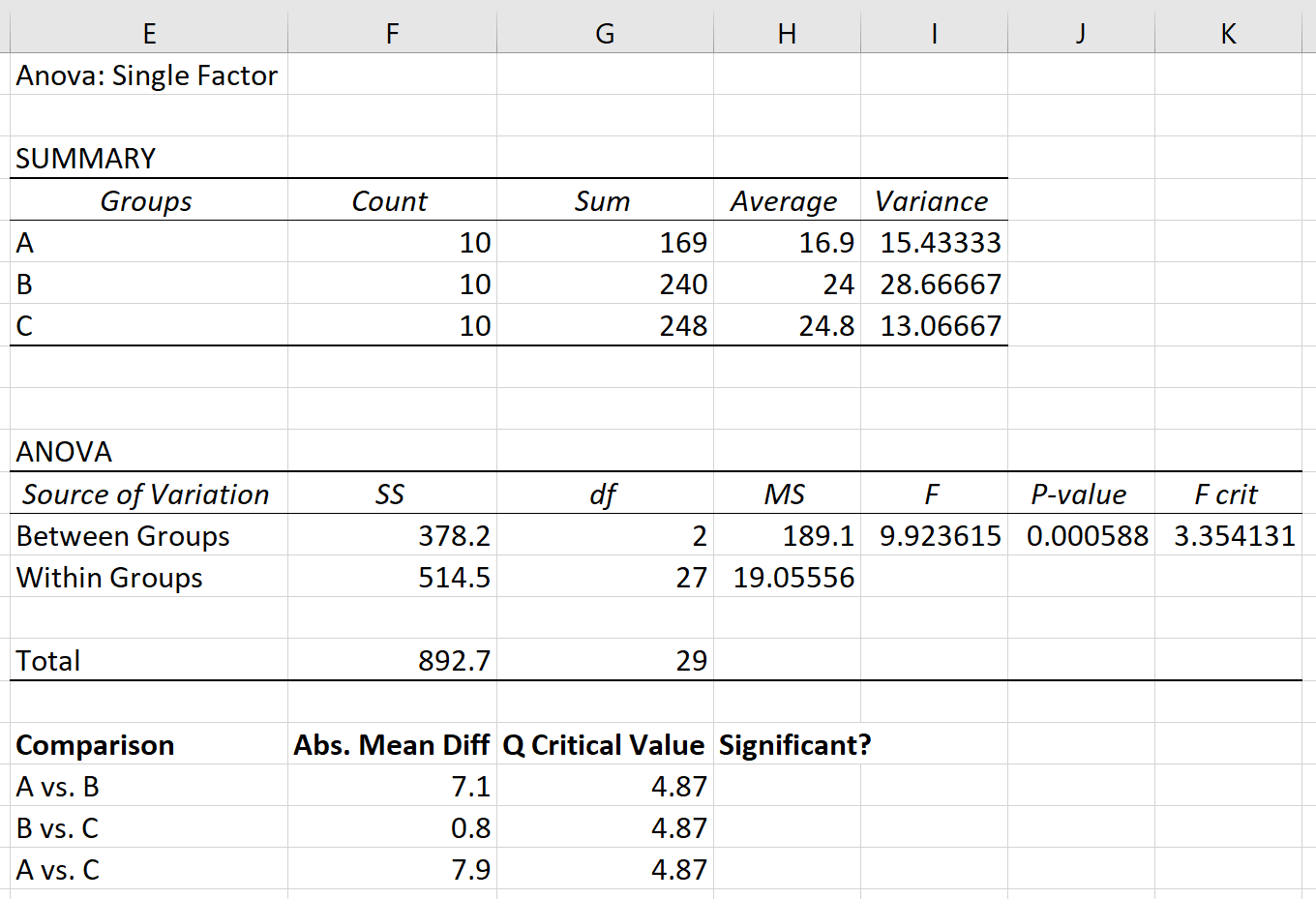
Załóżmy, że przeprowadzamy jednokierunkową ANOVA na trzech grupach: A, B i C. Wyniki jednokierunkowej ANOVA przedstawiono poniżej:

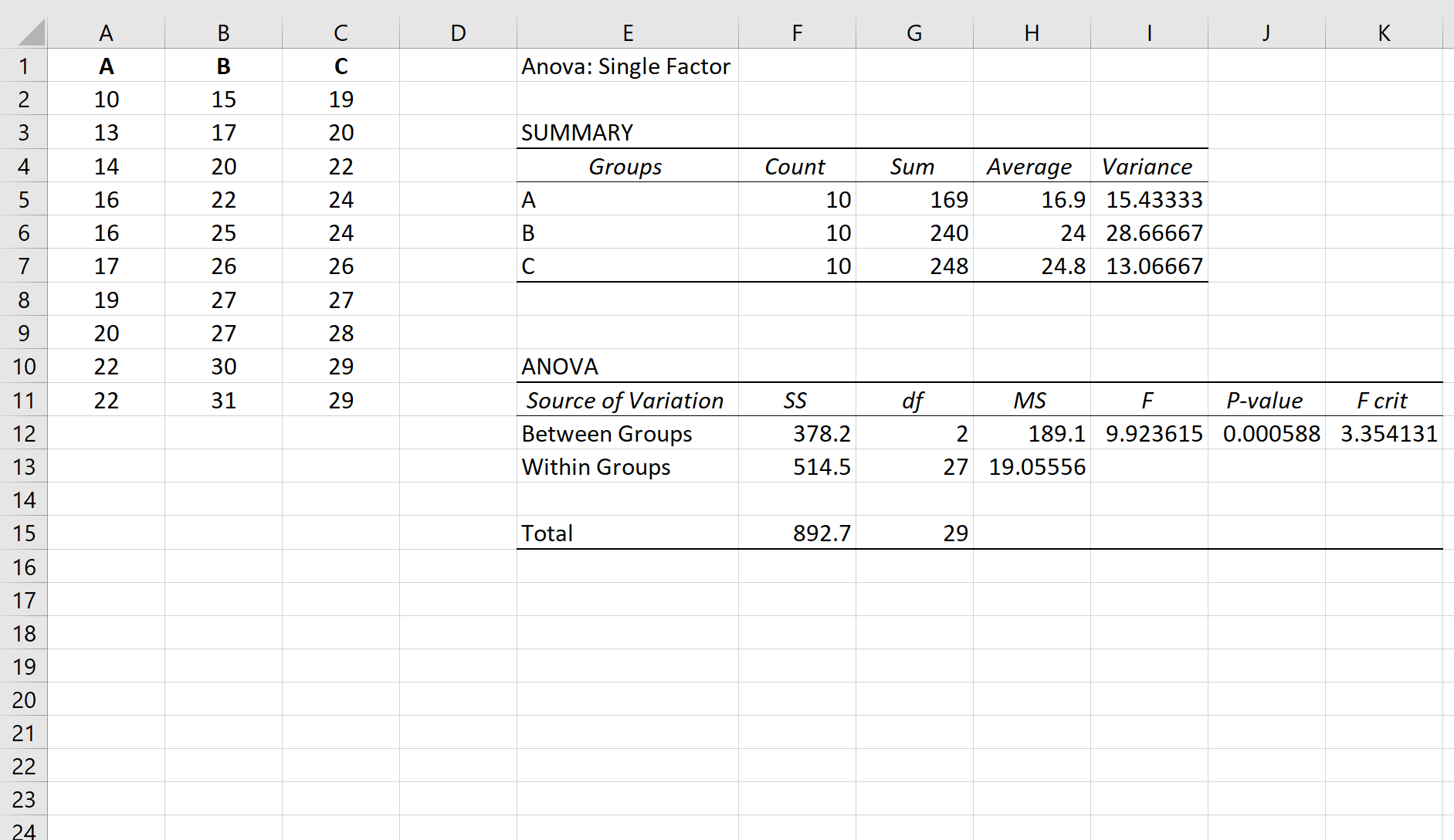
Powiązane: Jak wykonać jednokierunkową analizę wariancji w programie Excel

Wartość p tabeli ANOVA wynosi 0,000588 . Ponieważ ta wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową i stwierdzić, że średnie między trzema grupami nie są równe.

Aby dokładnie określić , które średnie grupowe są różne, możemy wykonać test post hoc Tukeya-Kramera, wykonując następujące kroki:

Krok 1: Znajdź średnią bezwzględną różnicę między każdą grupą.

Najpierw znajdziemy średnią bezwzględną różnicę między każdą grupą, korzystając ze średnich wymienionych w pierwszej tabeli wyniku ANOVA:

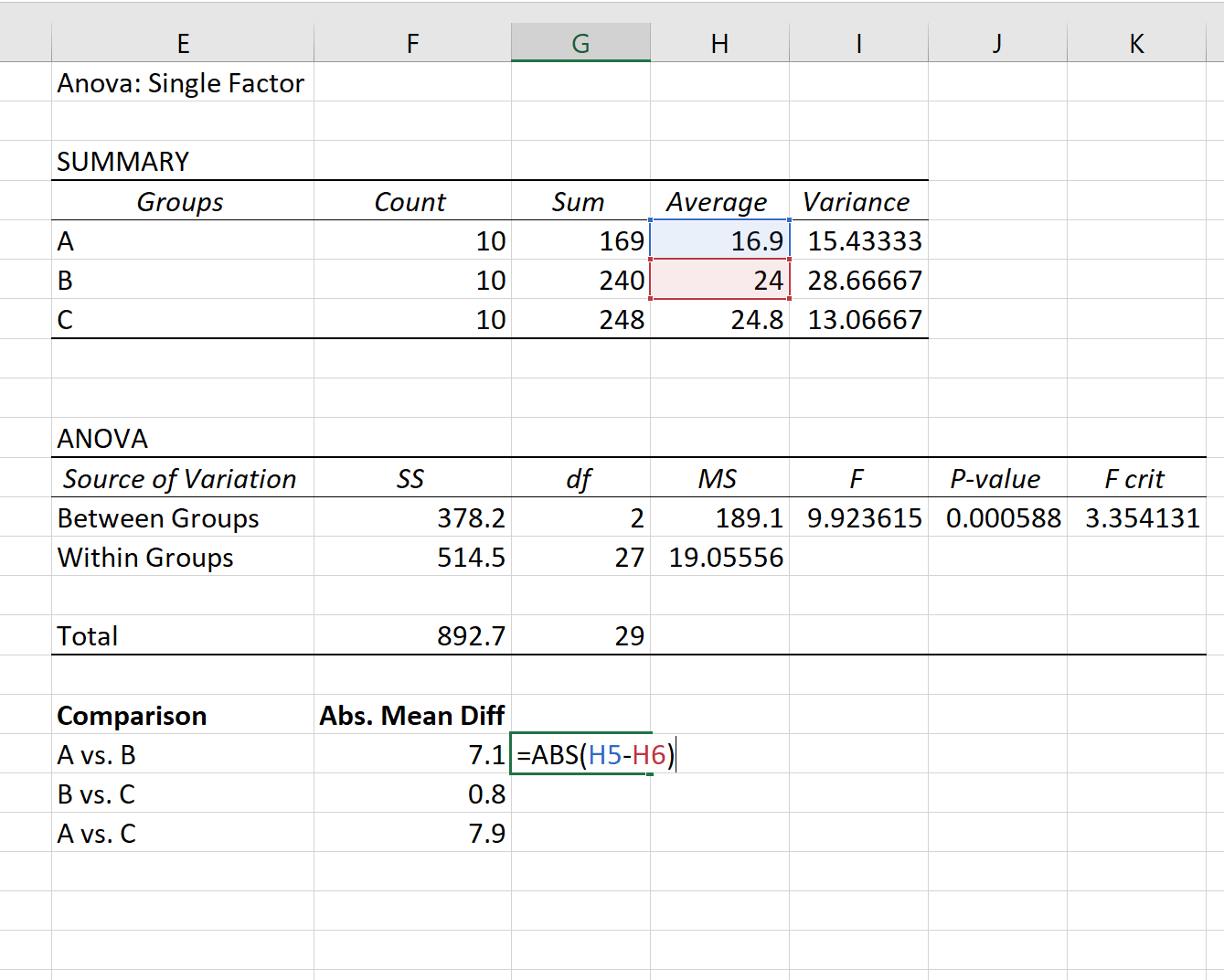
Krok 2: Znajdź wartość krytyczną Q.

Następnie musimy znaleźć wartość krytyczną Q, korzystając z następującego wzoru:

Wartość krytyczna Q = Q*√(s ² _zgrupowane / n.)

Złoto:

• Q = Wartość zakresu Tabeli Studenta Q
• s ² _połączone = wariancja zebrana dla wszystkich grup
• nie. = Wielkość próby dla danej grupy

Aby znaleźć wartość Q, możesz skorzystać z tabeli Studentized Range Q, która wygląda następująco:

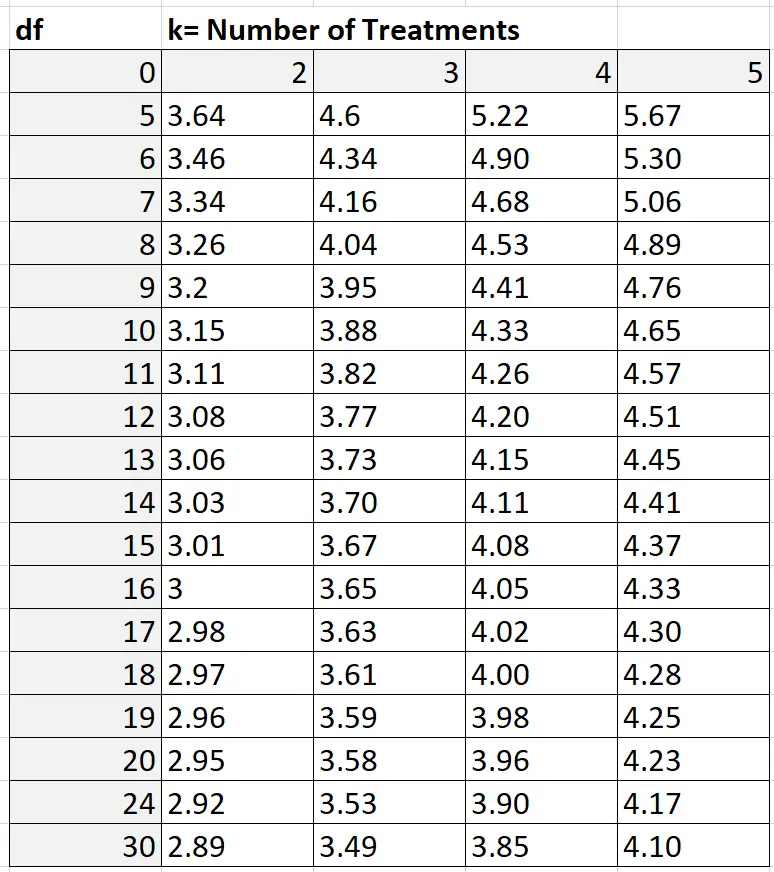
W naszym przykładzie k = liczba grup, tj. k = 3. Stopnie swobody obliczamy następująco: nk = 30 – 3 = 27. Ponieważ w powyższej tabeli nie pokazano 27, możemy zastosować ostrożne oszacowanie 24 Na podstawie k = 3 i df = 24 stwierdzamy, że Q = 3,53 .

Łączną wariancję można obliczyć jako średnią wariancji grup, która okazuje się wynosić 19,056 .

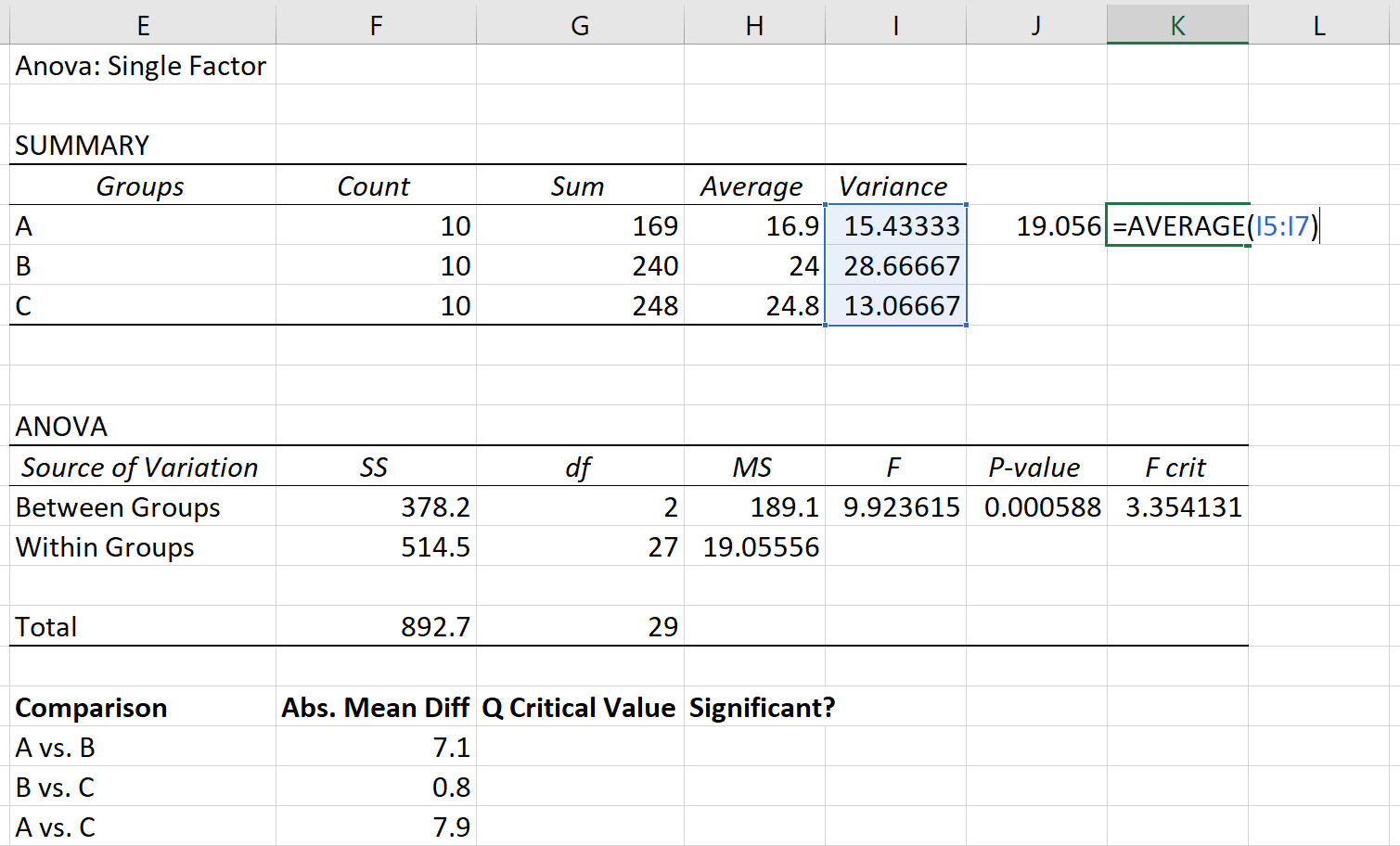
Ostatecznie wielkość próby w każdej grupie wynosi 10.

Zatem naszą wartość krytyczną Q można obliczyć w następujący sposób:

Wartość krytyczna Q = Q*√( ^s2 _zgrupowane / n.) = 3,53*√(19,056/10) = 4,87 .

Krok 3: Określ, które średnie grupowe są różne .

Na koniec możemy porównać średnią bezwzględną różnicę między każdą grupą z wartością krytyczną Q. Jeśli bezwzględna średnia różnica jest większa niż wartość krytyczna Q, wówczas różnica między średnimi grupowymi jest istotna statystycznie:

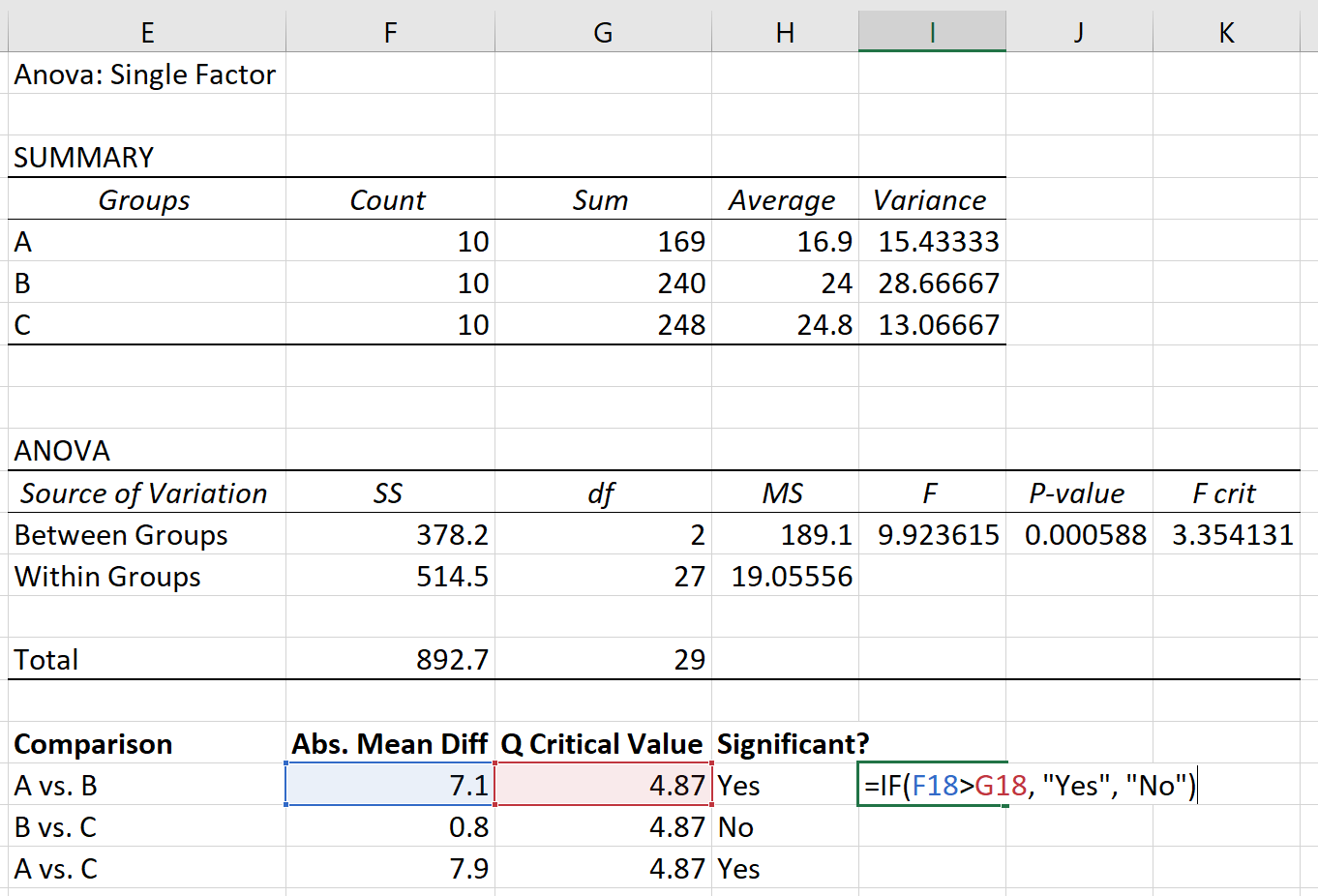
Na podstawie testu post hoc Tukeya-Kramera stwierdzono, co następuje:

• Różnica średnich pomiędzy grupą A i grupą B jest istotna statystycznie.
• Różnica średnich pomiędzy grupą B i grupą C nie jest istotna statystycznie.
• Różnica średnich pomiędzy grupą A i grupą C jest istotna statystycznie.

Dodatkowe zasoby

Jak wykonać jednokierunkową ANOVA w programie Excel
Przewodnik po korzystaniu z testów post-hoc z ANOVA