Twierdzenie czebyszewa

Przez Benjamin Anderson 5 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest twierdzenie Czebyszewa. Tutaj znajdziesz wzór na twierdzenie Czebyszewa, rozwiązane ćwiczenie oraz dodatkowo internetowy kalkulator twierdzenia Czebyszewa. Wreszcie pokazuje różnicę między twierdzeniem Czebyszewa a regułą empiryczną.

Jakie jest twierdzenie Czebyszewa?

Twierdzenie Czebyszewa , znane również jako nierówność Czebyszewa , jest regułą statystyczną służącą do obliczania prawdopodobieństwa, że wartość zmiennej losowej leży w pewnej odległości od jej średniej.

Innymi słowy, w statystyce twierdzenie Czebyszewa służy do określenia prawdopodobieństwa, że wartość mieści się w przedziale ufności.

Dodatkowo twierdzenie Czebyszewa służy również do udowadniania innych twierdzeń statystycznych, takich jak prawo wielkich liczb.

Chociaż twierdzenie Czebyszewa zostało po raz pierwszy sformułowane przez Francuza Irénée-Jules Bienaymé, nazwa twierdzenia wzięła się od jego sformułowania w 1867 r. przez Rosjanina Pafnuty’ego Czebushewa.

Wzór twierdzenia Czebyszewa

Twierdzenie Czebyszewa mówi, że prawdopodobieństwo, że wartość będzie równa k odchyleń standardowych od średniej, jest większe lub równe jeden minus stosunek jeden podzielony przez k kwadrat.

Zatem wzór na twierdzenie Czebyszewa jest następujący:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

Złoto

$X$

jest wartością zmiennej losowej,

$\mu$

średnia arytmetyczna zmiennej,

$\sigma$

jego odchylenie standardowe i

$k$

liczba odchyleń standardowych od średniej, dla której należy obliczyć prawdopodobieństwo.

Należy zauważyć, że tego wzoru można użyć tylko wtedy, gdy liczba odchyleń standardowych, na podstawie których przeprowadzane są obliczenia, jest większa niż 1, czyli innymi słowy, jeśli k jest większe niż 1.

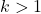$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ Aby obliczyć prawdopodobieństwo, możesz skorzystać z poniższego kalkulatora twierdzenia Czebyszewa dostępnego online.

Przykład twierdzenia Czebyszewa

Kiedy już poznaliśmy definicję twierdzenia Czebyszewa i jego wzór, oto rozwiązany przykład tego twierdzenia statystycznego, aby lepiej zrozumieć tę koncepcję.

Jeśli oceny uzyskane w statystykach kursów uniwersyteckich definiuje się za pomocą rozkładu ze średnią 65 i odchyleniem standardowym 10, jaki procent studentów uzyskał oceny pomiędzy 50 a 80?

Aby rozwiązać ten problem, musimy zastosować wzór twierdzenia Czebyszewa. Musimy jednak najpierw określić, ile odchyleń standardowych wartości 50 i 80 od średniej zmiennej, aby to zrobić, wystarczy wykonać następujące obliczenia:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

Zatem wartości 50 i 80 odpowiadają odpowiednio 1,5 odchylenia standardowego od średniej dolnej i górnej. Korzystamy zatem ze wzoru twierdzenia Czebyszewy dla k=1,5:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

Tym samym co najmniej 55,56% uczniów uzyskało oceny pomiędzy 50 a 80.

Kalkulator twierdzenia Czebyszewa

Wprowadź liczbę odchyleń standardowych między danymi wartościami a średnią (k) , a następnie kliknij „Oblicz”. Kalkulator zwróci wówczas minimalne prawdopodobieństwo przedziału ufności.

Należy wprowadzić liczbę odchyleń standardowych, stosując kropkę jako separator dziesiętny.

Twierdzenie Czebyszewa i praktyczna zasada

Dwa blisko powiązane pojęcia w statystyce to twierdzenie Czebyszewa i reguła empiryczna, ponieważ oba są używane do obliczania prawdopodobieństwa przedziałów ufności.

Różnica między twierdzeniem Czebyszewa a regułą empiryczną polega na tym, że twierdzenie Czebyszewa można zastosować w przypadku dowolnego rodzaju rozkładu, podczas gdy reguła empiryczna obowiązuje tylko dla rozkładu normalnego.

Zastosowanie twierdzenia Czebyszewa jest zatem szersze, ale reguła empiryczna zapewnia dokładniejsze wyniki dla rozkładu normalnego.

Kliknij tutaj, aby zobaczyć dokładnie, jaka jest praktyczna zasada:

➤ Zobacz: zasada ogólna

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej