Jak zastosować twierdzenie czebyszewa w programie excel

Twierdzenie Czebyszewa stwierdza, że dla dowolnej liczby k większej od 1 co najmniej 1 – 1/k ² wartości danych w dowolnym wyuczonym rozkładzie mieści się w k odchyleniach standardowych od średniej.

Przykładowo dla dowolnego rozkładu kształtowego co najmniej 1 – 1/3 ² = 88,89% wartości w rozkładzie będzie mieścić się w granicach 3 odchyleń standardowych od średniej.

W tym samouczku zaprezentowano kilka przykładów zastosowania twierdzenia Czebyszewa w programie Excel.

Przykład 1: Użyj twierdzenia Czebyszewa, aby określić, jaki procent wartości będzie mieścić się w przedziale od 30 do 70 dla zbioru danych ze średnią 50 i odchyleniem standardowym 10.

Najpierw określ wartość k. Możemy to zrobić, określając, ile odchyleń standardowych mieści się w przedziale od 30 do 70 od średniej:

(30 – średnia) / odchylenie standardowe = (30 – 50) / 10 = -20 / 10 = -2

(70 – średnia) / odchylenie standardowe = (70 – 50) / 10 = 20 / 10 = 2

Wartości 30 i 70 to odpowiednio 2 odchylenia standardowe poniżej i powyżej średniej. Zatem k = 2 .

Możemy wówczas skorzystać z poniższej formuły w programie Excel, aby znaleźć minimalny procent wartości mieszczących się w granicach 2 odchyleń standardowych od średniej dla tego zbioru danych:

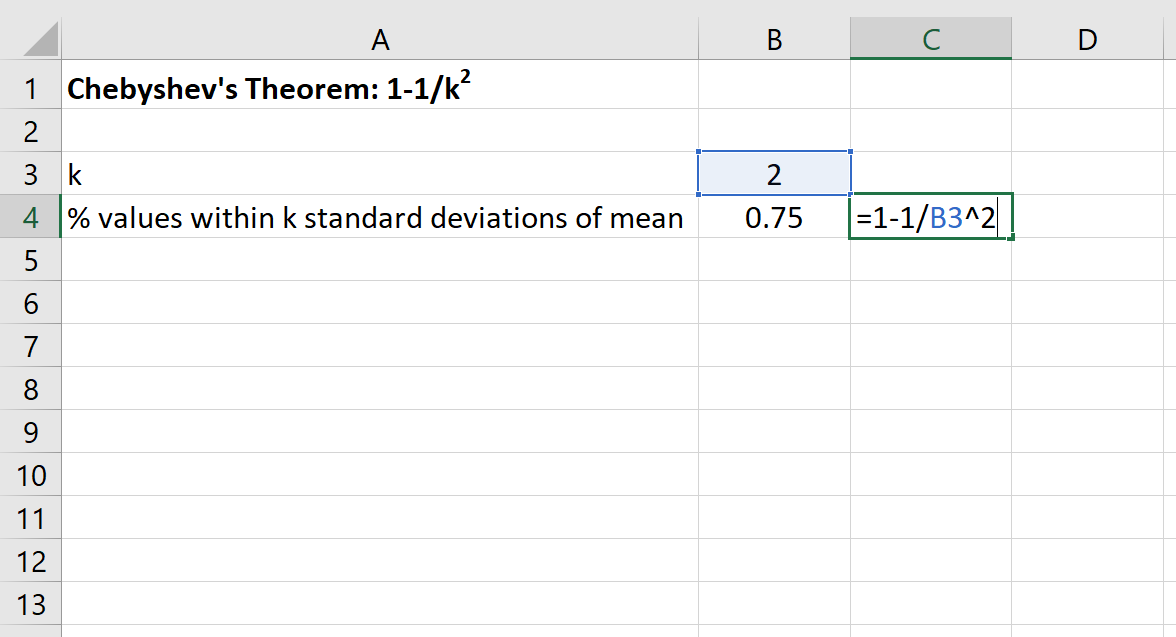
Procent wartości od 30 do 70 dla tego zbioru danych będzie wynosić co najmniej 75% .

Przykład 2: Użyj twierdzenia Czebyszewa, aby określić, jaki procent wartości będzie mieścić się w przedziale od 20 do 50 dla zbioru danych ze średnią 35 i odchyleniem standardowym 5.

Najpierw określ wartość k. Możemy to zrobić, określając, ile odchyleń standardowych mieści się w przedziale od 20 do 50 od średniej:

(20 – średnia) / odchylenie standardowe = (20 – 35) / 5 = -15 / 5 = -3

(50 – średnia) / odchylenie standardowe = (50 – 35) / 5 = 15 / 5 = 3

Wartości 20 i 50 to odpowiednio 3 odchylenia standardowe poniżej i powyżej średniej. Zatem k = 3 .

Możemy wówczas skorzystać z poniższej formuły w programie Excel, aby znaleźć minimalny procent wartości mieszczących się w granicach 3 odchyleń standardowych od średniej dla tego zbioru danych:

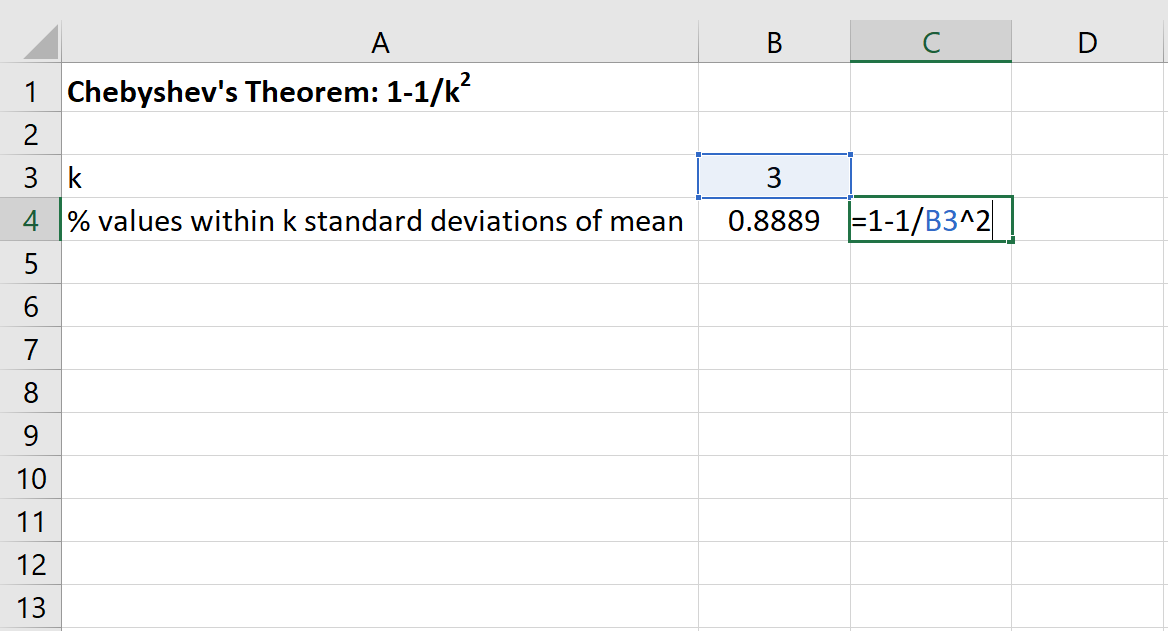
Procent wartości od 20 do 50 dla tego zbioru danych wyniesie co najmniej 88,89% .

Przykład 3: Użyj twierdzenia Czebyszewa, aby określić, jaki procent wartości będzie mieścić się w przedziale od 80 do 120 dla zbioru danych ze średnią 100 i odchyleniem standardowym 5.

Najpierw określ wartość k. Możemy to zrobić, określając, ile odchyleń standardowych mieści się w przedziale od 80 do 120 od średniej:

(80 – średnia) / odchylenie standardowe = (80 – 100) / 5 = -20 / 5 = -4

(120 – średnia) / odchylenie standardowe = (120 – 100) / 5 = 20 / 5 = 4

Wartości 80 i 120 to odpowiednio 4 odchylenia standardowe poniżej i powyżej średniej. Zatem k = 4 .

Możemy wówczas skorzystać z poniższej formuły w programie Excel, aby znaleźć minimalny procent wartości mieszczących się w granicach 4 odchyleń standardowych od średniej dla tego zbioru danych:

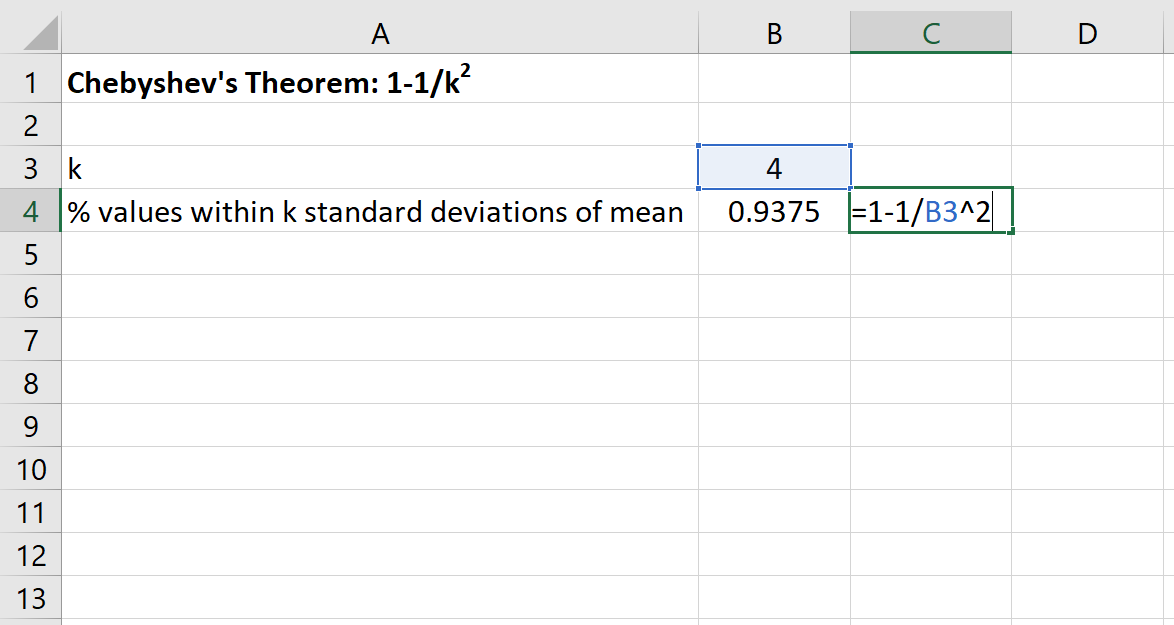
Procent wartości od 80 do 120 dla tego zbioru danych wyniesie co najmniej 93,75% .