Czym jest y hat w statystykach?

W statystyce termin y hat (zapisany ŷ ) odnosi się do szacowanej wartości zmiennej odpowiedzi w modelu regresji liniowej .

Zwykle piszemy szacunkowe równanie regresji w następujący sposób:

ŷ = β ₀ + β ₁ x

Złoto:

• ŷ : Szacowana wartość zmiennej odpowiedzi
• β ₀ : Średnia wartość zmiennej odpowiedzi, gdy zmienna predykcyjna wynosi zero
• β ₁ : średnia zmiana zmiennej odpowiedzi związana ze wzrostem o jedną jednostkę zmiennej predykcyjnej

Załóżmy na przykład, że mamy następujący zbiór danych, który pokazuje liczbę godzin przestudiowanych przez sześciu różnych uczniów wraz z ich wynikami z egzaminu końcowego:

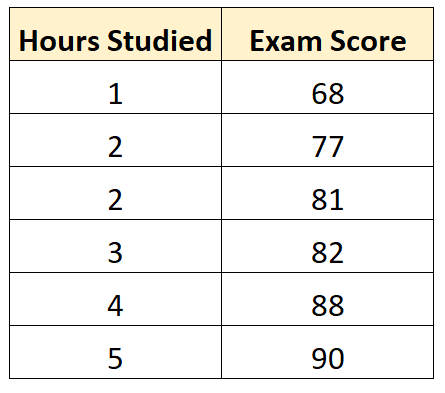
Załóżmy, że używamy oprogramowania statystycznego (takiego jak R , Excel , Python lub nawet ręcznie), aby dopasować następujący model regresji, wykorzystując godziny studiowane jako zmienną predykcyjną i wyniki egzaminu jako zmienną odpowiedzi:

Wynik = 66,615 + 5,0769*(Godziny)

Sposób interpretacji współczynników regresji w tym modelu jest następujący:

• Średni wynik egzaminu studenta studiującego zero godzin wynosi 66 615 .
• Wynik egzaminu zwiększa się średnio o 5,0769 punktów za każdą dodatkową przestudiowaną godzinę.

Możemy użyć tego równania regresji, aby oszacować wynik danego ucznia na podstawie liczby przestudiowanych godzin.

Przykładowo, student studiujący 3 godziny powinien uzyskać wynik:

Wynik = 66,615 + 5,0769*(3) = 81,85

Dlaczego używany jest Y Hat?

Symbol „kapelusza” w statystykach służy do oznaczenia dowolnego „szacunkowego” terminu. Na przykład ŷ oznacza szacunkową zmienną odpowiedzi.

Zazwyczaj dopasowując modele regresji liniowej, używamy próbki danych z populacji, ponieważ jest to wygodniejsze i mniej czasochłonne niż zbieranie danych dla każdej możliwej obserwacji w populacji.

Kiedy więc znajdujemy równanie regresji, szacujemy jedynie prawdziwy związek między zmienną predykcyjną a zmienną odpowiedzi.

Dlatego w równaniu regresji używamy terminu ŷ zamiast y.

Dodatkowe zasoby

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Wprowadzenie do zmiennych objaśniających i odpowiedzi