Jak wykonać jednokierunkową anova w sas

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

W tym samouczku przedstawiono krok po kroku przykład wykonania jednokierunkowej analizy ANOVA w SAS-ie.

Krok 1: Utwórz dane

Załóżmy, że badacz rekrutuje 30 studentów do udziału w badaniu. Studenci są losowo przydzielani do stosowania jednej z trzech metod nauki w celu przygotowania się do egzaminu.

Wyniki egzaminu dla poszczególnych uczniów przedstawiono poniżej:

Do utworzenia tego zbioru danych w SAS-ie możemy użyć następującego kodu:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Krok 2: Wykonaj jednokierunkową ANOVA

Następnie użyjemy proc ANOVA do wykonania jednokierunkowej ANOVA:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

Uwaga : Użyliśmy funkcji średniej , aby określić, że należy przeprowadzić test post-hoc Tukeya, jeśli całkowita wartość p z jednoczynnikowej analizy ANOVA jest statystycznie istotna.

Krok 3: Interpretacja wyników

Pierwszą tabelą, którą chcemy przeanalizować w wynikach, jest tabela ANOVA:

Z tej tabeli możemy zobaczyć:

• Ogólna wartość F: 5,26
• Odpowiednia wartość p: 0,0140

Przypomnijmy, że jednokierunkowa analiza ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : Wszystkie średnie grupowe są równe.
• H _A : Co najmniej jedna średnia grupowa jest inna   odpoczynek.

Ponieważ wartość p tabeli ANOVA (0,0140) jest mniejsza niż α = 0,05, odrzucamy hipotezę zerową.

To mówi nam, że średni wynik egzaminu nie jest równy w przypadku trzech metod badania.

Powiązane: Jak interpretować wartość F i wartość P w ANOVA

SAS udostępnia także wykresy skrzynkowe umożliwiające wizualizację rozkładu wyników egzaminów dla każdej z trzech metod badania:

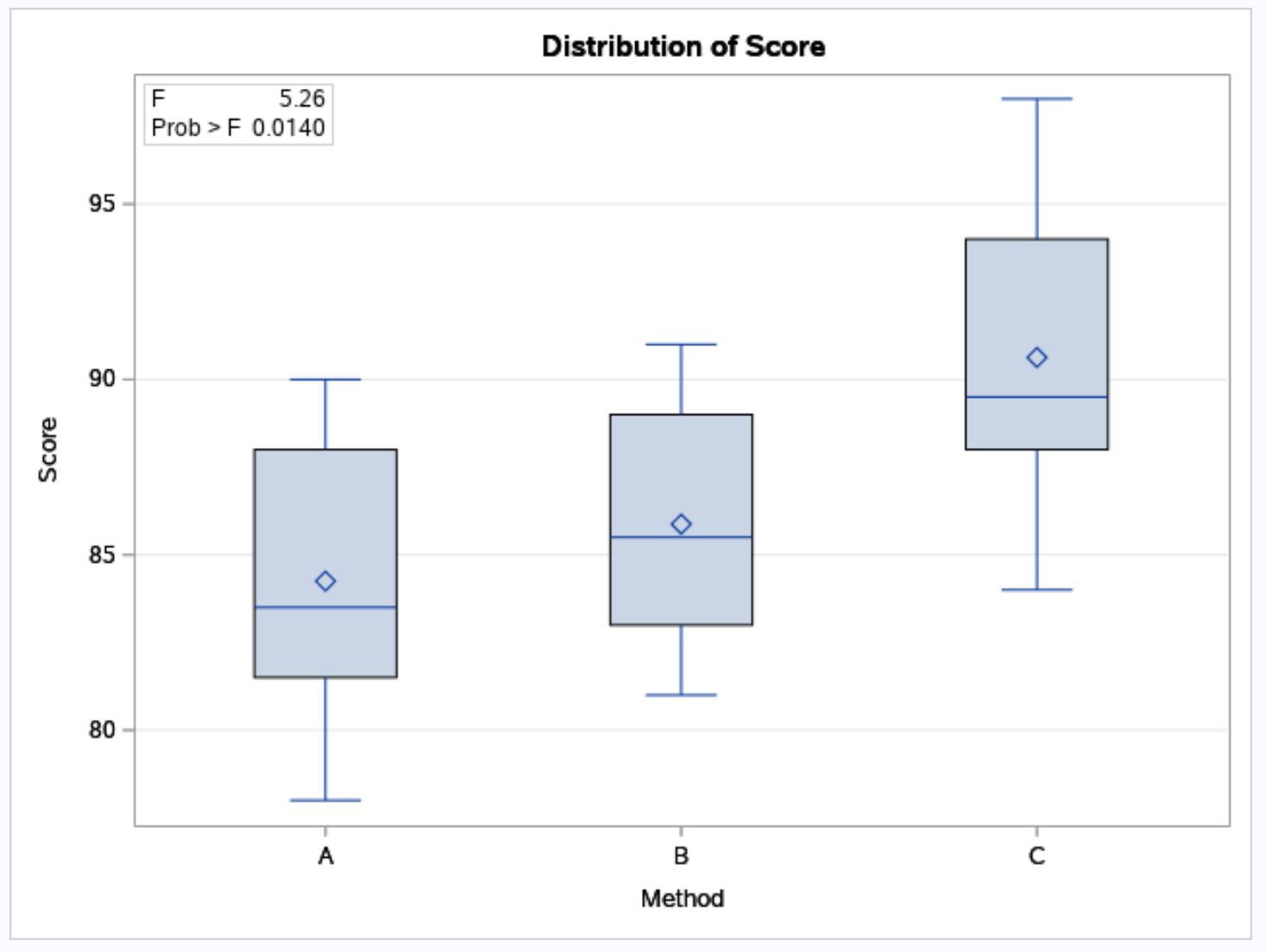
Z wykresów pudełkowych widać, że wyniki egzaminów są zwykle wyższe wśród uczniów, którzy stosowali metodę nauki C w porównaniu z metodami B i C.

Aby dokładnie określić, które średnie grupowe są różne, należy odwołać się do tabeli wyników końcowych, która przedstawia wyniki testów post-hoc Tukeya:

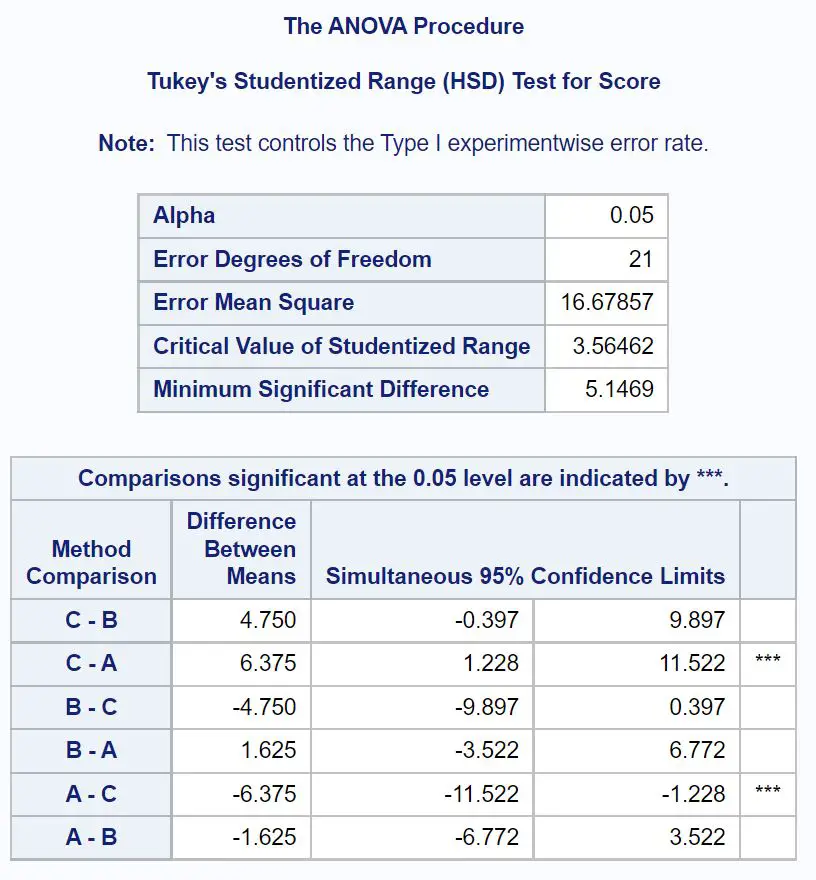
Aby dowiedzieć się, które średnie grupowe są różne, musimy sprawdzić, które porównania parami mają obok siebie gwiazdki ( *** ).

Z tabeli wynika, że średnie wartości grup A i C różnią się istotnie statystycznie.

Możemy również zobaczyć 95% przedział ufności dla różnicy średnich wyników egzaminów pomiędzy grupami A i C:

95% przedział ufności dla średniej różnicy: [1,228, 11,522]

Krok 4: Zgłoś wyniki

Na koniec możemy zgłosić wyniki jednokierunkowej analizy ANOVA:

Przeprowadzono jednoczynnikową analizę ANOVA w celu porównania wpływu trzech różnych metod badawczych na wyniki badania.

Jednoczynnikowa analiza ANOVA wykazała, że istniała statystycznie istotna różnica w średnim wyniku egzaminu pomiędzy co najmniej dwiema grupami (F(2,21) = [5,26], p = 0,014).

Test HSD Tukeya do porównań wielokrotnych ujawnił, że średnia wartość wyniku egzaminu różniła się istotnie pomiędzy metodą C i metodą A (95% CI = [1,228, 11,522]).

Nie było statystycznie istotnej różnicy w średnich wynikach egzaminu pomiędzy metodą A i metodą B lub pomiędzy metodą B i metodą C.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat jednokierunkowej analizy ANOVA:

Wprowadzenie do jednokierunkowej ANOVA
Jednokierunkowy kalkulator ANOVA
Jak ręcznie wykonać jednokierunkową ANOVA