Jak wykonać jednokierunkową anova w programie excel
Jednoczynnikową ANOVA („analiza wariancji”) stosuje się w celu ustalenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.
W tym samouczku wyjaśniono, jak przeprowadzić jednokierunkową analizę ANOVA w programie Excel.
Przykład: jednokierunkowa ANOVA w Excelu
Załóżmy, że badacz rekrutuje 30 studentów do udziału w badaniu. Studenci są losowo przydzielani do stosowania jednej z trzech technik uczenia się w ciągu następnych trzech tygodni w celu przygotowania się do egzaminu. Pod koniec trzech tygodni wszyscy uczniowie przystępują do tego samego testu.
Poniżej znajdują się wyniki testów uczniów:
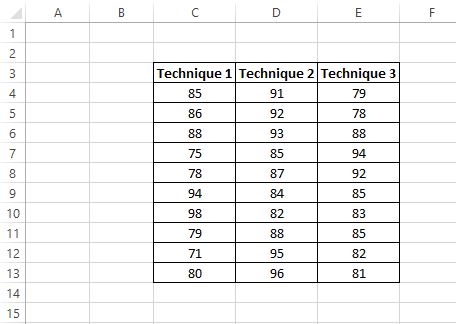
Badacz chce przeprowadzić jednoczynnikową analizę ANOVA, aby określić, czy średnie wyniki są takie same w trzech grupach.
Aby wykonać jednokierunkową ANOVA w programie Excel, przejdź do zakładki Dane , a następnie kliknij opcję Analiza danych w grupie Analiza .
Jeśli nie widzisz opcji Analiza danych , musisz najpierw załadować darmowe oprogramowanieAnalysis ToolPak .

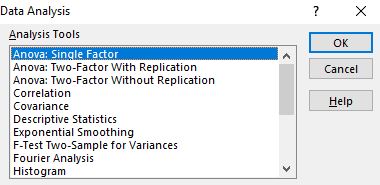
Po kliknięciu pojawi się okno z różnymi opcjami skanera. Wybierz opcję Anova: Single Factor , a następnie kliknij przycisk OK .
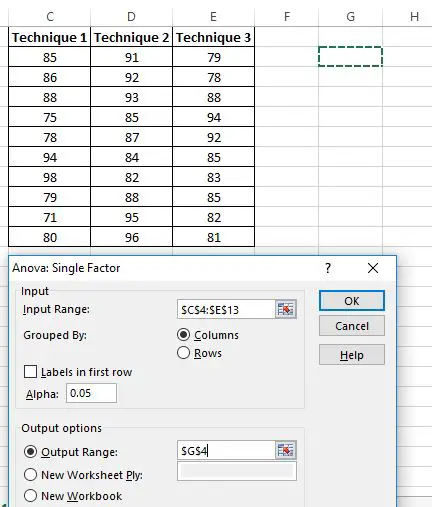
Pojawi się nowe okno z pytaniem o zakres wejściowy . Możesz przeciągnąć ramkę wokół danych lub ręcznie wprowadzić zakres danych. W tym przypadku nasze dane znajdują się w komórkach C4:E13 .
Następnie wybierz poziom Alpha dla testu. Domyślnie liczba ta wynosi 0,05. W tym przypadku zostawię go na poziomie 0,05.
Na koniec wybierz komórkę dla Zakresu wyjściowego , w której pojawią się jednokierunkowe wyniki ANOVA. W tym przypadku wybieram komórkę G4 .
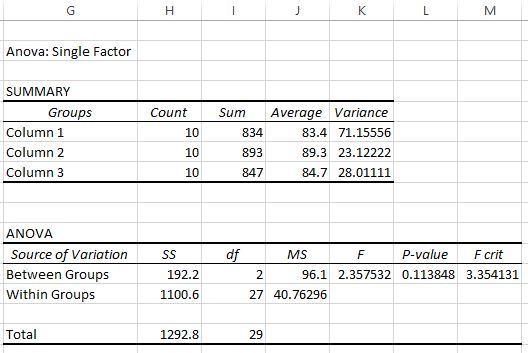
Po kliknięciu OK pojawi się jednokierunkowy wynik ANOVA:
Interpretacja wyniku
W wynikach zostaną wyświetlone dwie tabele. Pierwsza to tabela podsumowująca, która pokazuje liczbę wyników testów w każdej grupie, sumę wyników testów, średnią wyników testów i wariancję wyników testów.
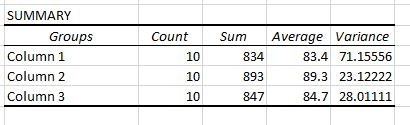
Przypomnijmy, że jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej grup.
Z tej pierwszej tabeli widzimy, że średni wynik dla każdej z trzech grup jest inny, ale aby wiedzieć, czy te różnice są istotne statystycznie, musimy spojrzeć na drugą tabelę.
Druga tabela przedstawia statystykę testu F, krytyczną wartość F i wartość p:
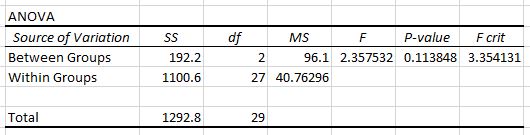
W tym przypadku statystyka testu F wynosi 2,3575 , a wartość krytyczna F wynosi 3,3541 . Ponieważ statystyka testu F jest mniejsza niż wartość krytyczna F, nie mamy wystarczających dowodów, aby odrzucić hipotezę zerową, że średnie z trzech grup są równe.
Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje różnica w wynikach testów pomiędzy trzema technikami badawczymi.
Aby dojść do tego samego wniosku, moglibyśmy również użyć wartości p . W tym przypadku wartość p wynosi 0,1138 , czyli jest wyższa niż poziom alfa wynoszący 0,05 .
Oznacza to, że nie mamy wystarczających dowodów, aby odrzucić hipotezę zerową, że średnie trzech grup są równe.
Uwaga: W przypadku odrzucenia hipotezy zerowej można przeprowadzić test post hoc Tukeya-Kramera , aby dokładnie określić, które średnie grupowe są różne.