Jak przeprowadzić jednokierunkową anova w spss

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.

Ten typ testu nazywa się jednokierunkową ANOVA, ponieważ analizujemy wpływ zmiennej predykcyjnej na zmienną odpowiedzi.

Gdybyśmy zamiast tego byli zainteresowani wpływem dwóch zmiennych predykcyjnych na zmienną odpowiedzi, moglibyśmy przeprowadzić dwuczynnikową analizę ANOVA .

W tym samouczku wyjaśniono, jak przeprowadzić jednokierunkową analizę ANOVA w SPSS.

Przykład: jednokierunkowa ANOVA w SPSS

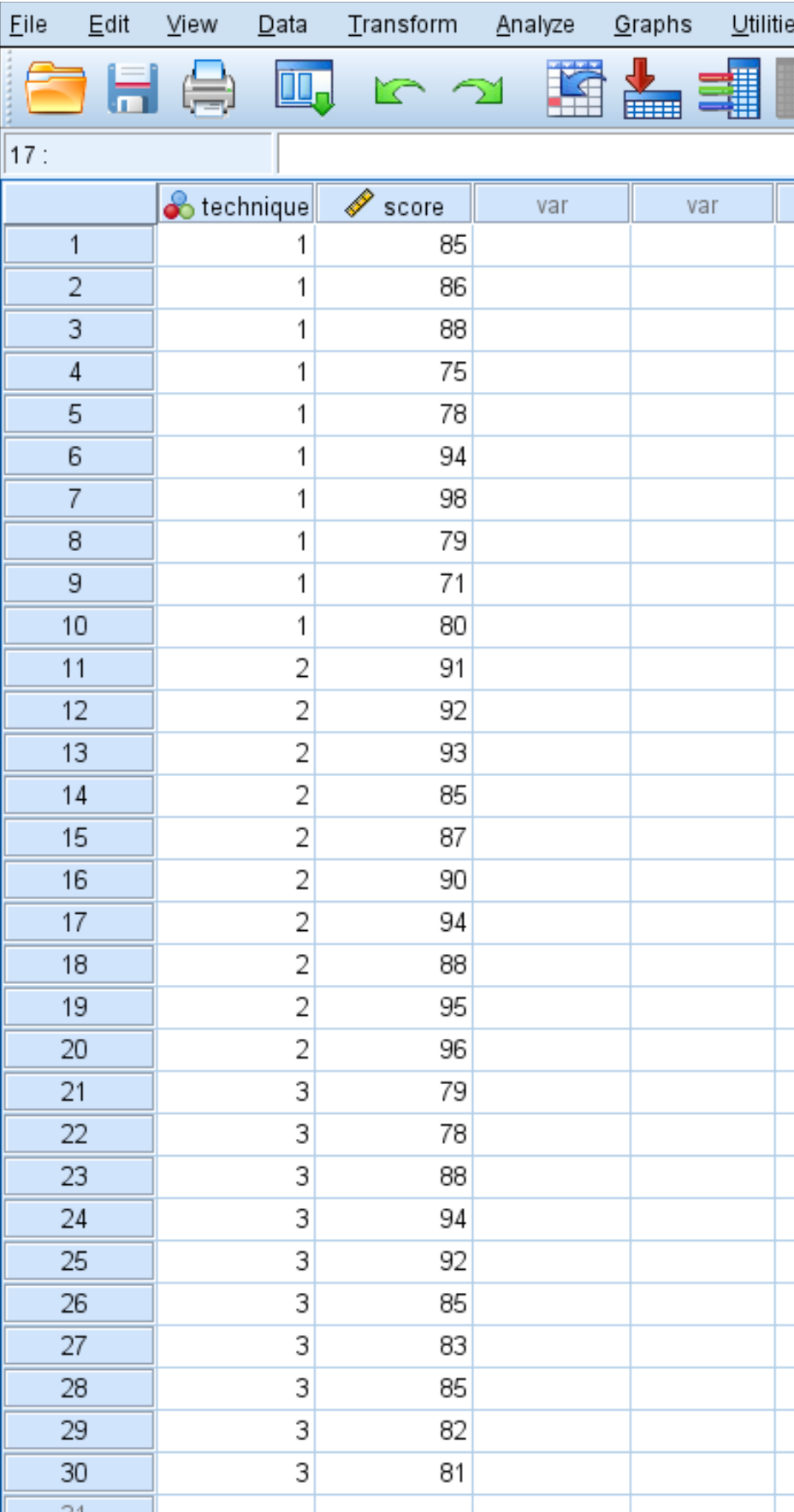
Załóżmy, że badacz rekrutuje 30 studentów do udziału w badaniu. Studenci są losowo przydzielani do stosowania jednej z trzech technik nauki w następnym miesiącu, aby przygotować się do egzaminu. Pod koniec miesiąca wszyscy uczniowie przystępują do tego samego testu.

Poniżej znajdują się wyniki testów uczniów:

Wykonaj poniższe kroki, aby wykonać jednoczynnikową analizę ANOVA w celu ustalenia, czy średnie wyniki są takie same w trzech grupach.

Krok 1: Wizualizuj dane.

Najpierw utworzymy wykresy pudełkowe , aby zwizualizować rozkład wyników testów dla każdej z trzech technik badawczych. Kliknij kartę Wykresy , a następnie kliknij opcję Kreator wykresów .

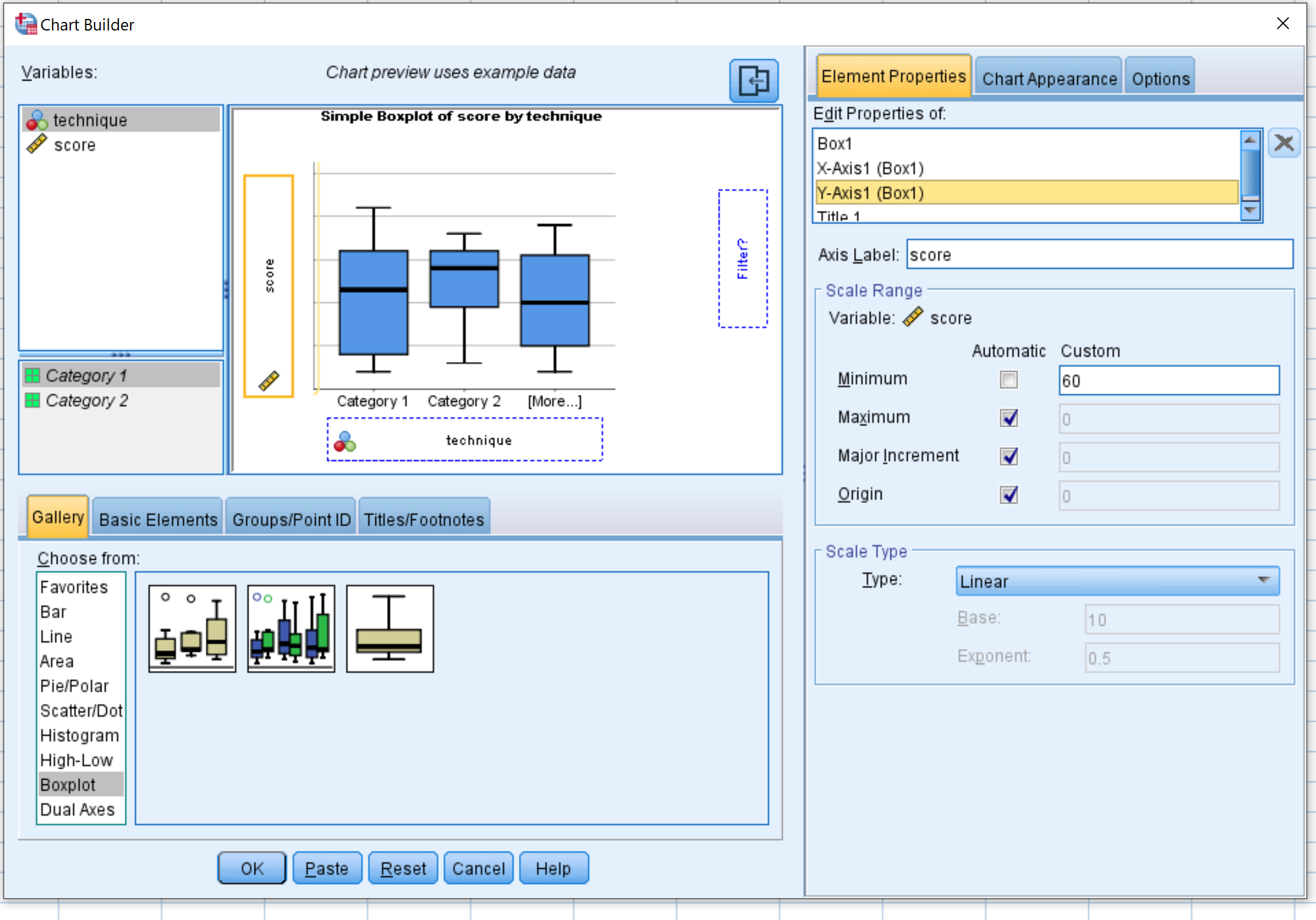
Wybierz Boxplot w oknie Wybierz z:. Następnie przeciągnij pierwszy wykres oznaczony jako Simple boxplot do głównego okna edycji. Przeciągnij zmienną techniczną na oś x i wynik na oś y.

Następnie kliknij Właściwości elementu , a następnie kliknij Oś Y1 . Zmień wartość minimalną na 60. Następnie kliknij OK .

Pojawią się następujące wykresy pudełkowe:

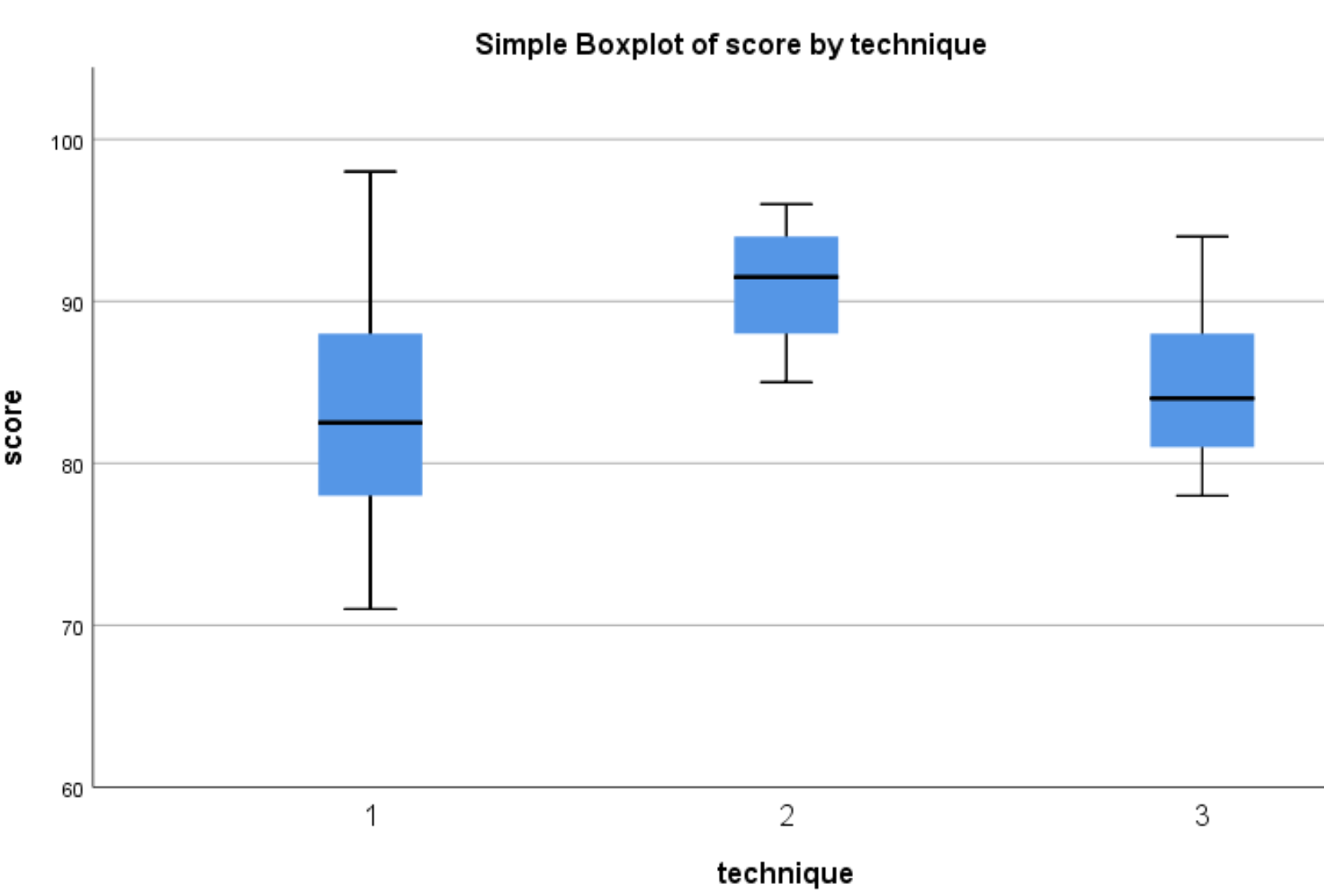
Widzimy, że rozkład wyników testów jest zwykle wyższy w przypadku uczniów, którzy korzystali z Techniki 2, niż dla uczniów, którzy korzystali z Technik 1 i 3. Aby określić, czy te różnice w wynikach są istotne statystycznie, przeprowadzimy jednokierunkową ANOVA.

Krok 2: Wykonaj jednokierunkową ANOVA.

Kliknij kartę Analiza , następnie Porównaj średnie , a następnie Jednoczynnikowa ANOVA .

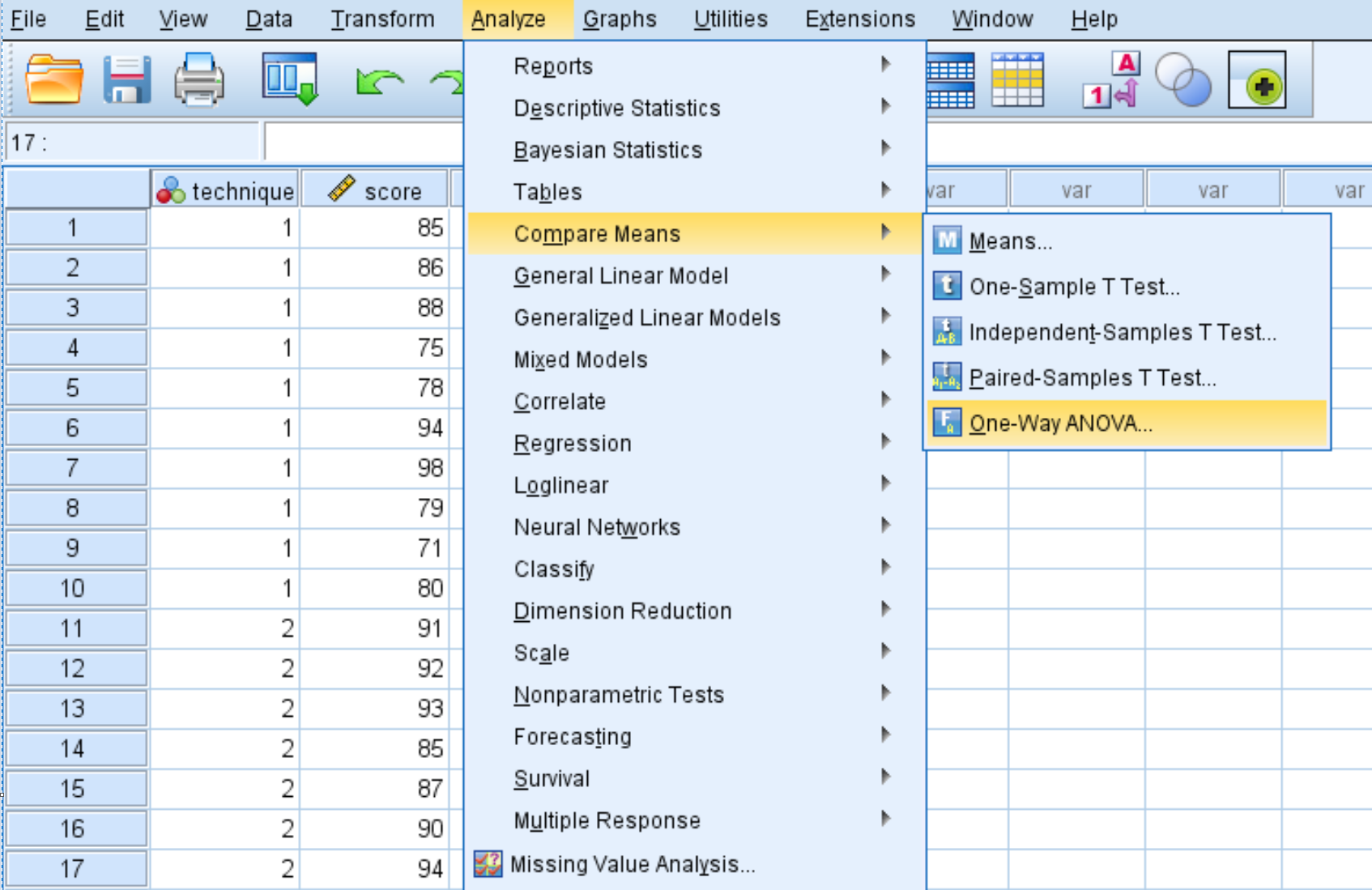
W nowym oknie, które się pojawi, umieść wynik zmiennej w polu „Lista zależna”, a technikę zmiennej w polu „Czynnik”.

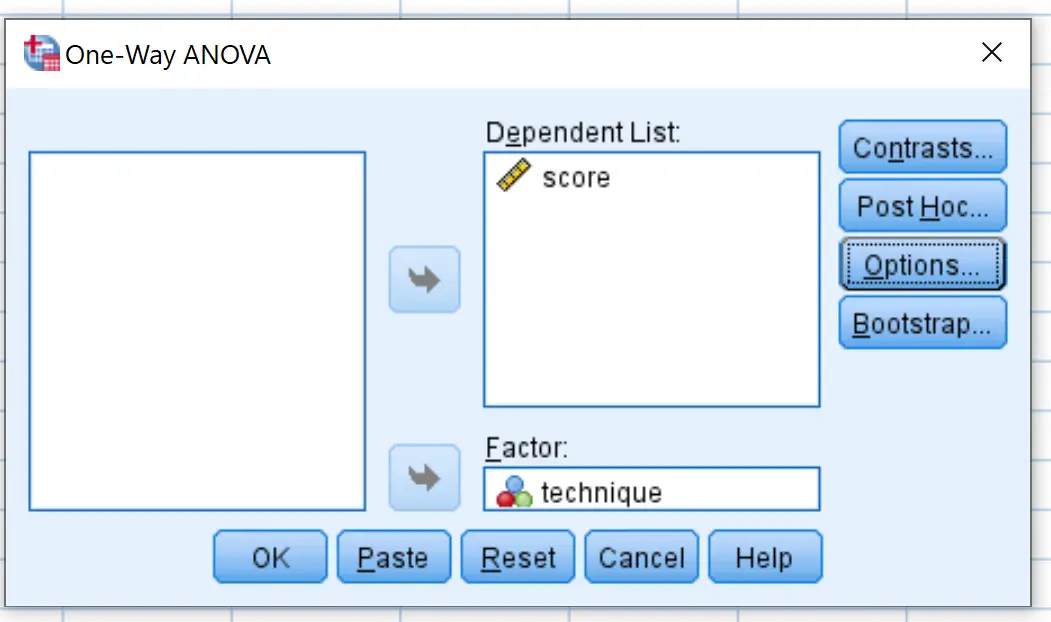
Następnie kliknij Post Hoc i zaznacz pole obok Tukey . Następnie kliknij Kontynuuj .

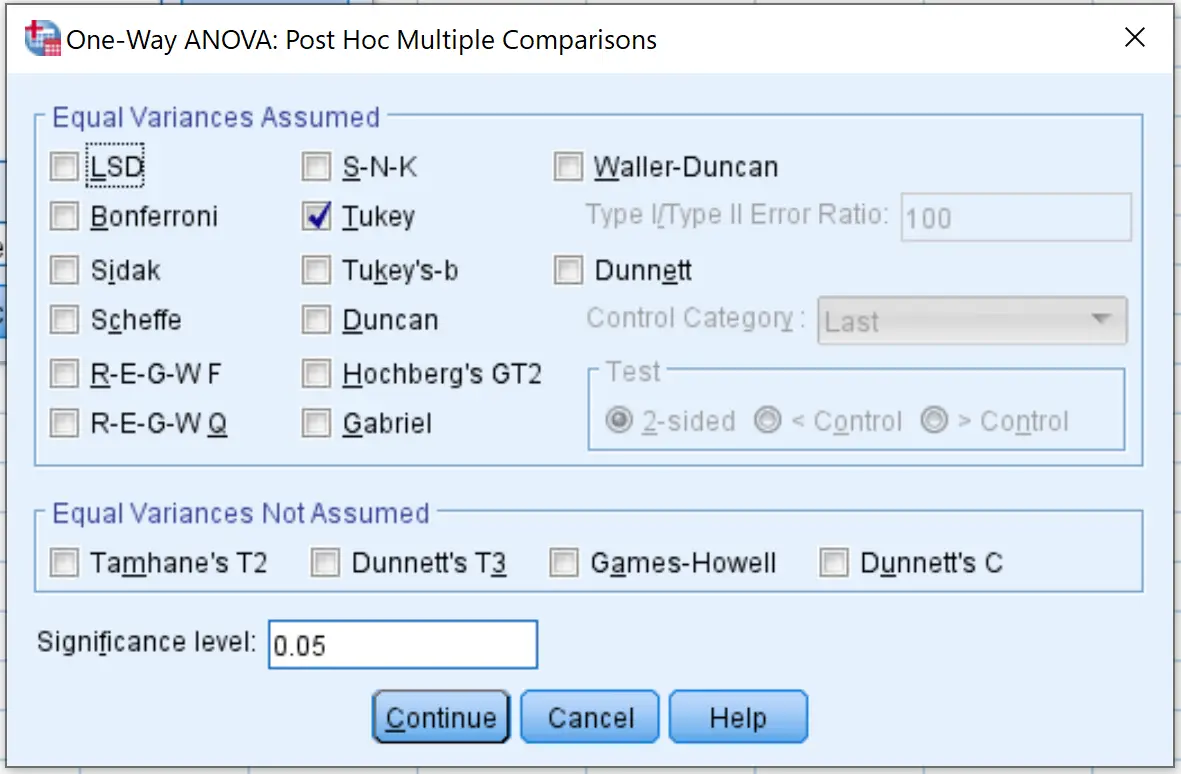
Następnie kliknij Opcje i zaznacz pole obok Opisowe . Następnie kliknij Kontynuuj .

Na koniec kliknij OK .

Krok 3: Zinterpretuj wynik.

Po kliknięciu OK pojawią się jednokierunkowe wyniki ANOVA. Oto jak zinterpretować wynik:

Opis tabeli

Ta tabela przedstawia statystyki opisowe dla każdej z trzech grup w naszym zbiorze danych.

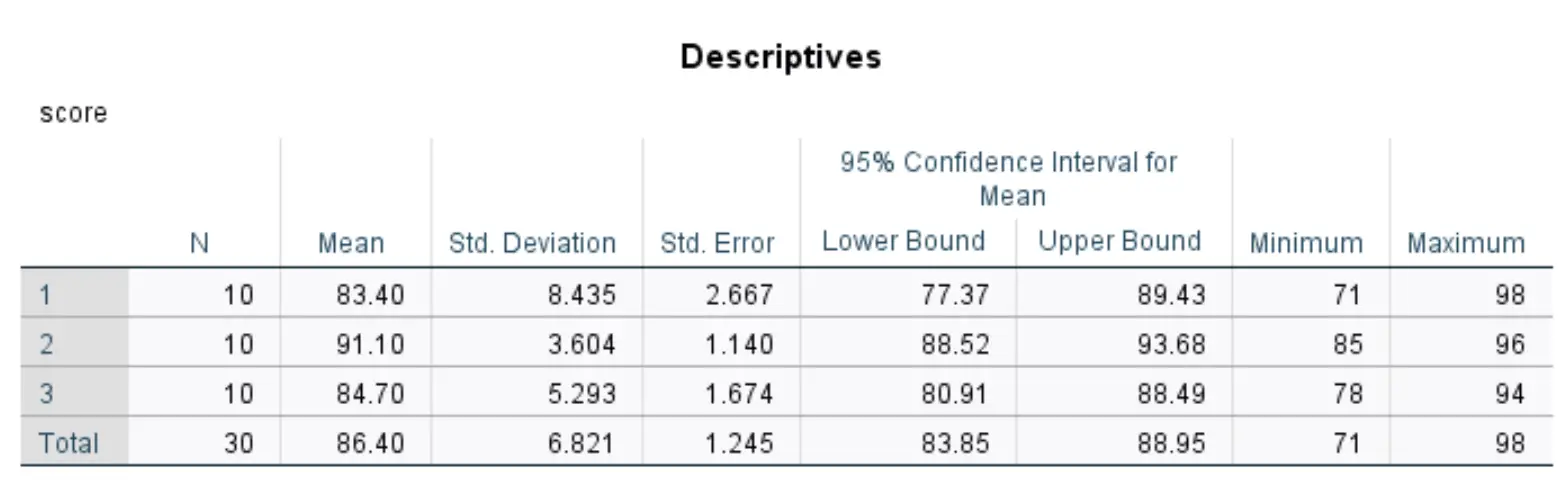
Najbardziej istotne liczby obejmują:

• N: Liczba uczniów w każdej grupie.
• Średnia: średni wynik testu dla każdej grupy.
• Standard. Odchylenie: Odchylenie standardowe wyników testu dla każdej grupy.

Tabela ANOVA

Poniższa tabela przedstawia wyniki jednoczynnikowej analizy ANOVA:

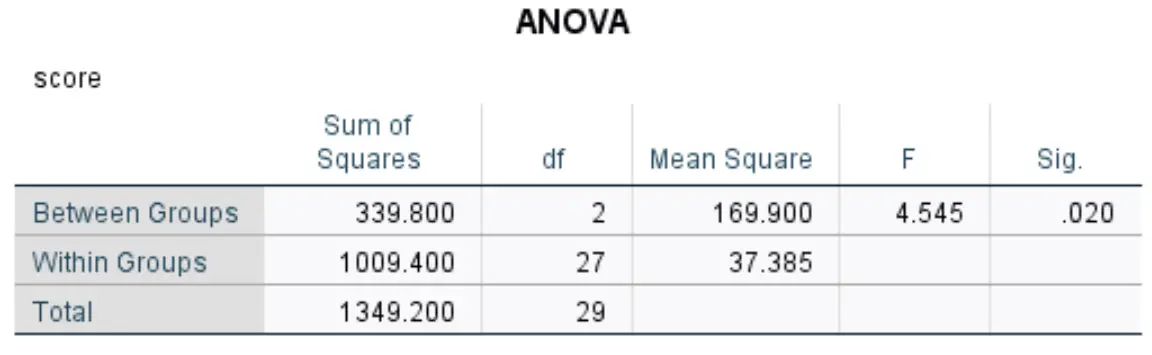
Najbardziej istotne liczby obejmują:

• F: Ogólna statystyka F.
• Sig: Wartość p odpowiadająca statystyce F (4,545) z licznikiem df (2) i mianownikiem df (27). W tym przypadku wartość p wynosi 0,020 .

Przypomnijmy, że jednokierunkowa analiza ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ (hipoteza zerowa): μ ₁ = μ ₂ = μ ₃ = … = μ _k (wszystkie średnie populacji są równe)
• _HA (hipoteza alternatywna): co najmniej jedna średnia populacji jest inna   odpoczynek

Ponieważ wartość p w tabeli ANOVA jest mniejsza niż 0,05, mamy wystarczające dowody, aby odrzucić hipotezę zerową i stwierdzić, że przynajmniej jedna ze średnich grupowych różni się od pozostałych.

Aby dokładnie wiedzieć, które średnie grupowe różnią się od siebie, możemy odwołać się do ostatniej tabeli wyniku ANOVA.

Wielokrotna tabela porównawcza

W tabeli tej przedstawiono wielokrotne porównania post hoc Tukeya pomiędzy każdą z trzech grup. Nas interesuje głównie Sig. kolumna, która wyświetla wartości p dla różnic średnich pomiędzy każdą grupą:

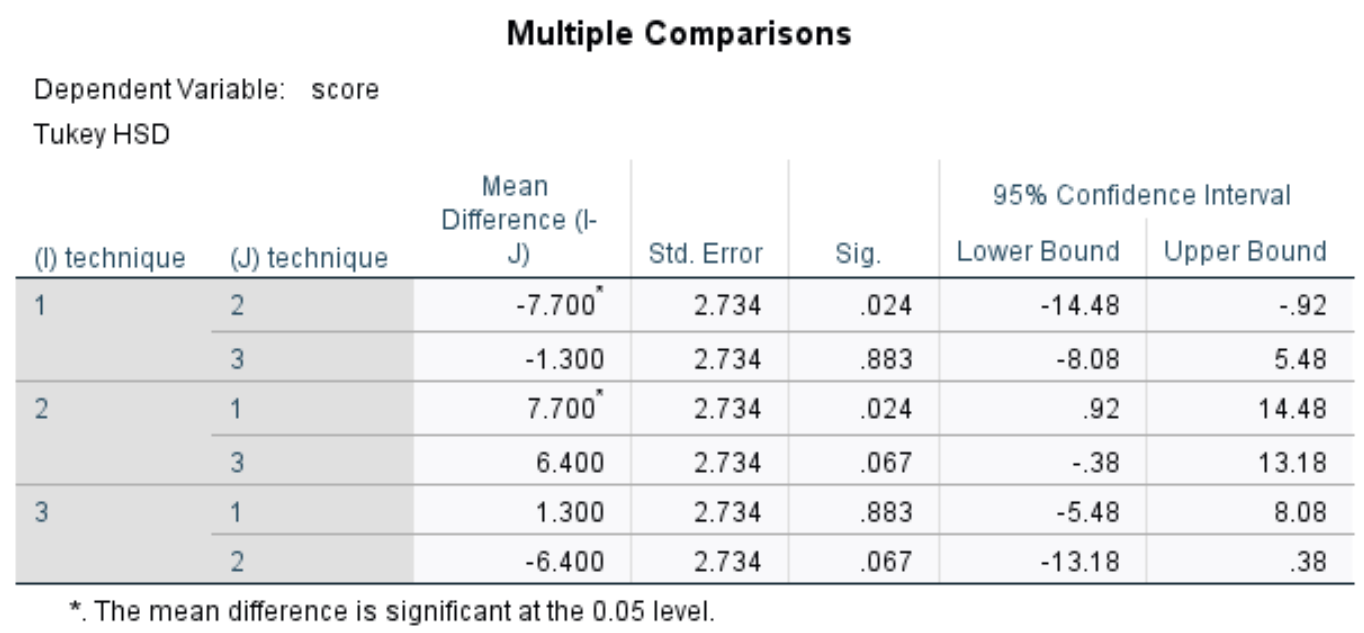
W tabeli możemy zobaczyć wartości p dla następujących porównań:

• Technika 1 kontra 2: | wartość p = 0,024
• Technika 1 na 3 | wartość p = 0,883
• Technika 2 na 3 | wartość p = 0,067

Jedyne porównanie grupowe z wartością p mniejszą niż 0,05 dotyczy Techniki 1 i Techniki 2.

To mówi nam, że istnieje statystycznie istotna różnica w średnich wynikach testów pomiędzy uczniami, którzy stosowali Technikę 1 i tymi, którzy stosowali Technikę 2.

Nie ma jednak statystycznie istotnej różnicy pomiędzy technikami 1 i 3, ani pomiędzy technikami 2 i 3.

Krok 4: Ogłoś wyniki.

Na koniec możemy zgłosić wyniki jednokierunkowej analizy ANOVA. Oto przykład, jak to zrobić:

Przeprowadzono jednoczynnikową analizę ANOVA w celu ustalenia, czy trzy różne techniki badawcze doprowadziły do różnych wyników testu.

W sumie 10 uczniów stosowało każdą z trzech technik nauki przez miesiąc, zanim wszyscy przystąpili do tego samego testu.

Jednoczynnikowa analiza ANOVA ujawniła, że istniała statystycznie istotna różnica w wynikach testów pomiędzy co najmniej dwiema grupami (F(2, 27) = 4,545, p = 0,020).

Test Tukeya do porównań wielokrotnych ujawnił, że średnie wyniki testów znacznie różniły się pomiędzy uczniami, którzy stosowali Technikę 1 i Technikę 2 (p = 0,024, 95% CI = [-14,48, -0,92]).

Nie stwierdzono istotnej statystycznie różnicy pomiędzy punktacją dla techniki 1 i 3 (p = 0,883) ani pomiędzy wynikami dla techniki 2 i 3 (p = 0,067).