Jak wykonać jednokierunkową anova w stata
Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.
Ten typ testu nazywa się jednokierunkową ANOVA, ponieważ analizujemy wpływ zmiennej predykcyjnej na zmienną odpowiedzi. Gdybyśmy zamiast tego byli zainteresowani wpływem dwóch zmiennych predykcyjnych na zmienną odpowiedzi, moglibyśmy przeprowadzić dwuczynnikową analizę ANOVA .
W tym samouczku wyjaśniono, jak wykonać jednokierunkową analizę ANOVA w Stata.
Przykład: jednokierunkowa ANOVA w Stata
W tym przykładzie użyjemy wbudowanego zbioru danych Stata zwanego skurczowym , aby wykonać jednoczynnikową analizę wariancji. Ten zbiór danych zawiera następujące trzy zmienne dla 58 różnych osób:
- Używany narkotyk
- Choroba pacjenta
- Zmiana skurczowego ciśnienia krwi
Poniższe kroki wykonamy w celu przeprowadzenia jednokierunkowej analizy ANOVA w celu ustalenia, czy rodzaj zastosowanego leku ma znaczący wpływ na zmianę skurczowego ciśnienia krwi.
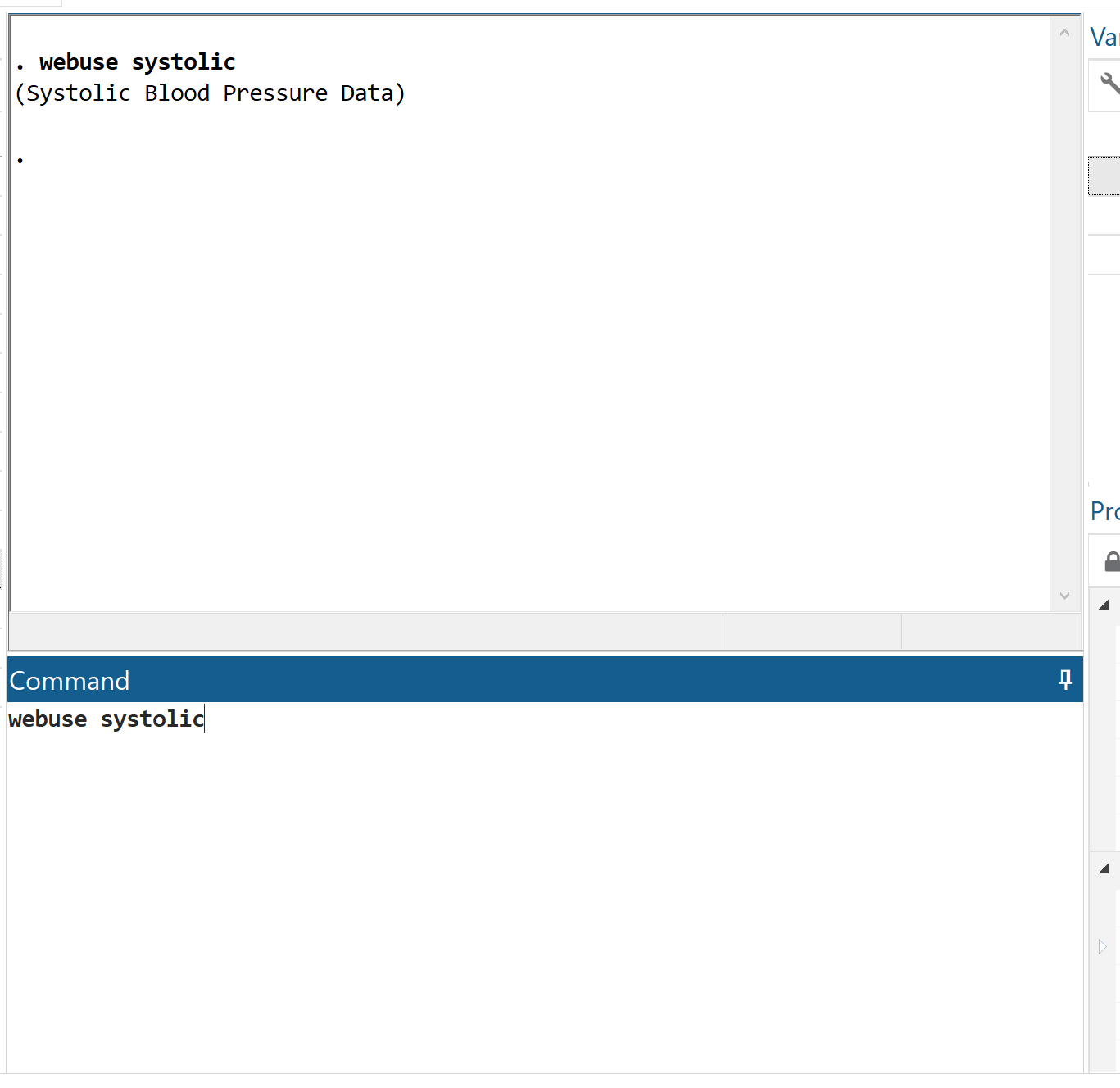
Krok 1: Załaduj dane.
Najpierw załaduj dane, wpisując webuse skurczowy w polu poleceń i klikając Enter.
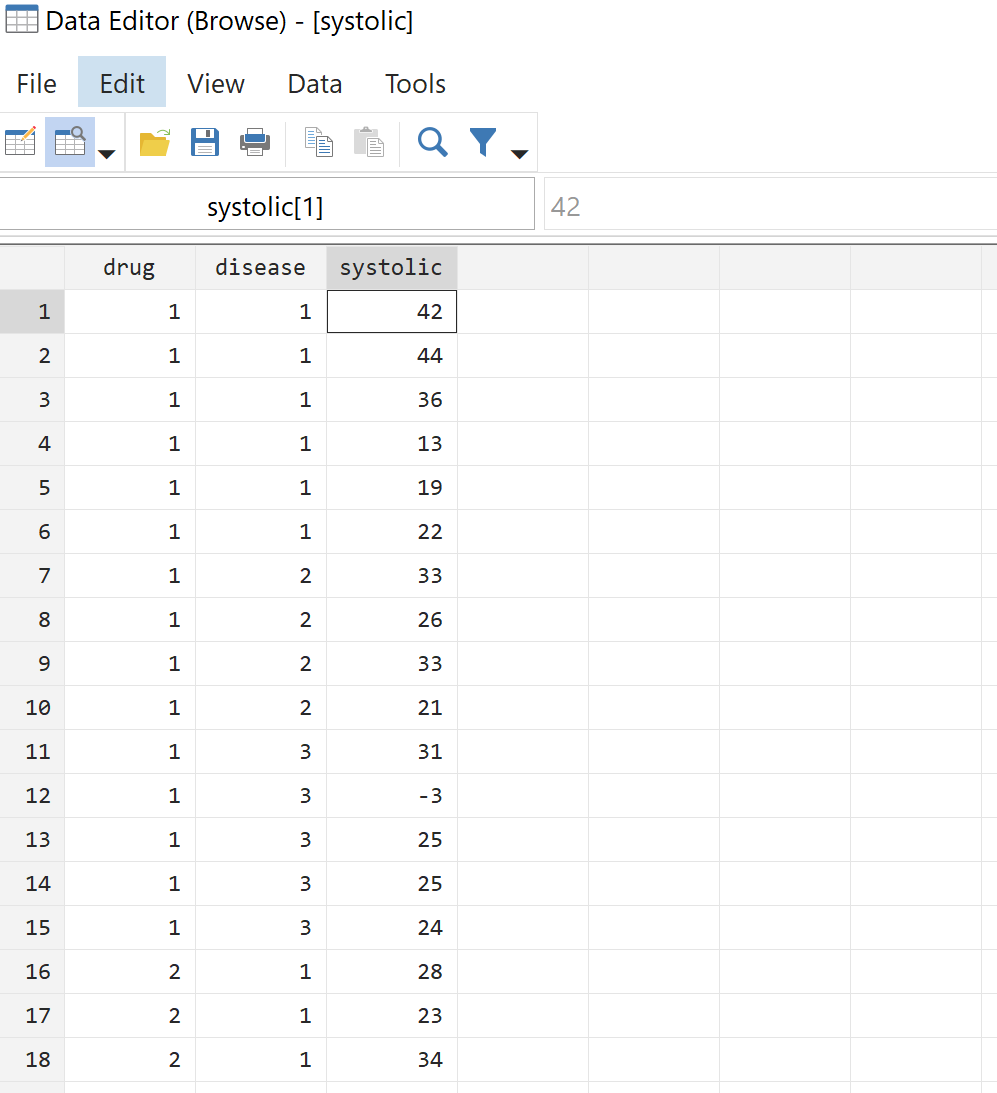
Krok 2: Wyświetl surowe dane.
Przed wykonaniem jednoczynnikowej analizy ANOVA przyjrzyjmy się najpierw surowym danym. Z górnego paska menu przejdź do opcji Dane > Edytor danych > Edytor danych (Przeglądaj) . To pokaże nam rzeczywiste dane dla wszystkich 58 pacjentów:
Krok 3: Wizualizuj dane.
Następnie zwizualizujmy dane. Stworzymy wykresy pudełkowe , aby wyświetlić rozkład wartości skurczowego ciśnienia krwi dla każdej kategorii leku.
Z górnego paska menu wybierz Wykresy > Wykres pudełkowy . W obszarze zmiennych wybierz opcję Skurczowe:
Następnie w podnagłówku Kategorie w zmiennej grupującej wybierz lek:
Kliknij OK . Wykres z czterema wykresami pudełkowymi zostanie automatycznie wyświetlony:
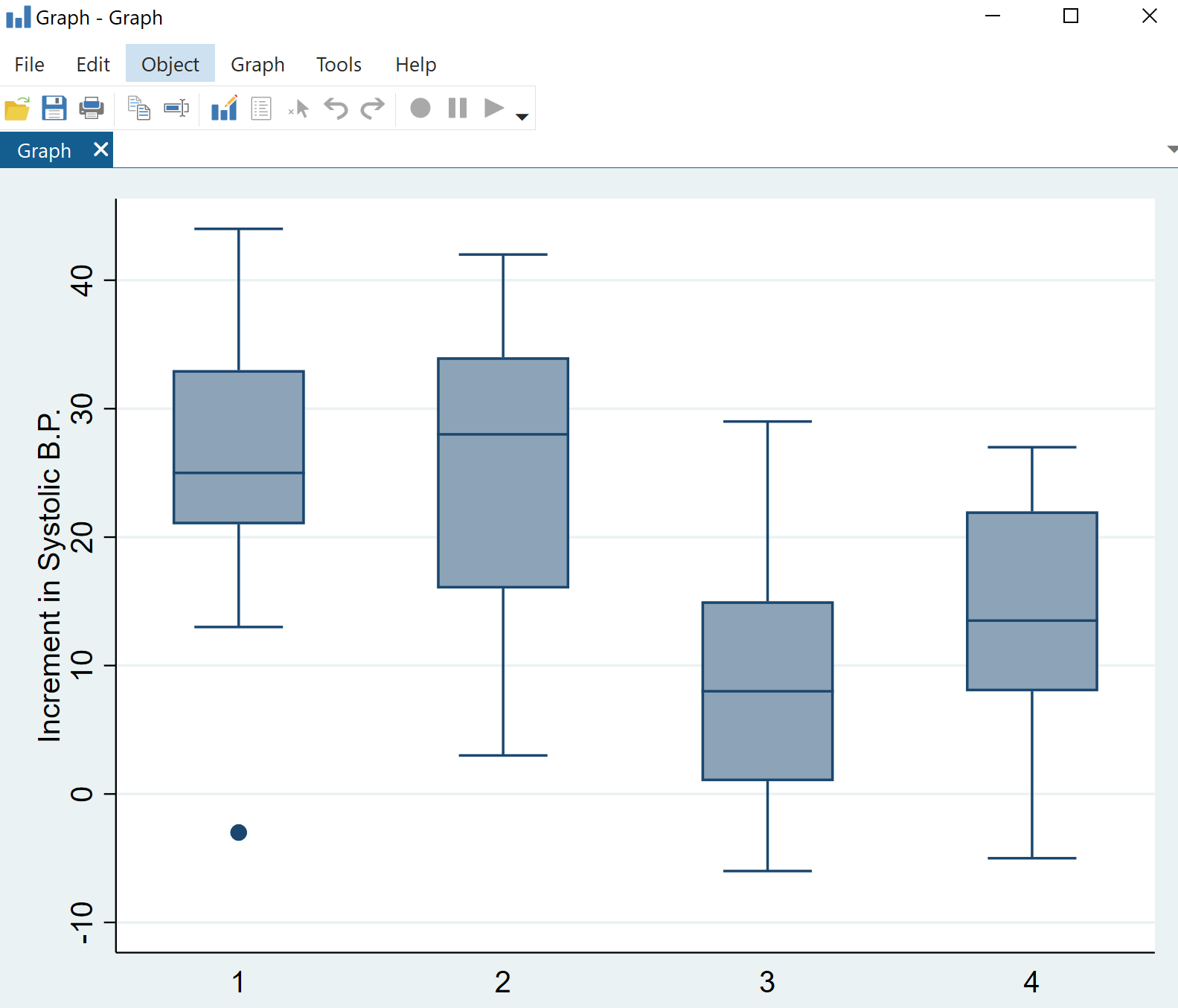
Od razu widać, że rozkład zmian skurczowego ciśnienia krwi różni się w zależności od kategorii leków, ale jednoczynnikowa analiza ANOVA powie nam, czy różnice te są istotne statystycznie.
Krok 4: Wykonaj jednokierunkową ANOVA.
Z górnego paska menu przejdź do Statystyki > Modele liniowe i pokrewne > ANOVA/MANOVA > Jednokierunkowa ANOVA .
W obszarze Zmienna odpowiedzi wybierz opcję Skurczowe. W obszarze zmiennej czynnikowej wybierz lek. Następnie kliknij pole obok opcji Utwórz tabelę podsumowującą, abyśmy mogli zobaczyć podstawowe statystyki opisowe dla każdej grupy. Następnie kliknij OK .
Wyświetlone zostaną następujące dane wyjściowe:
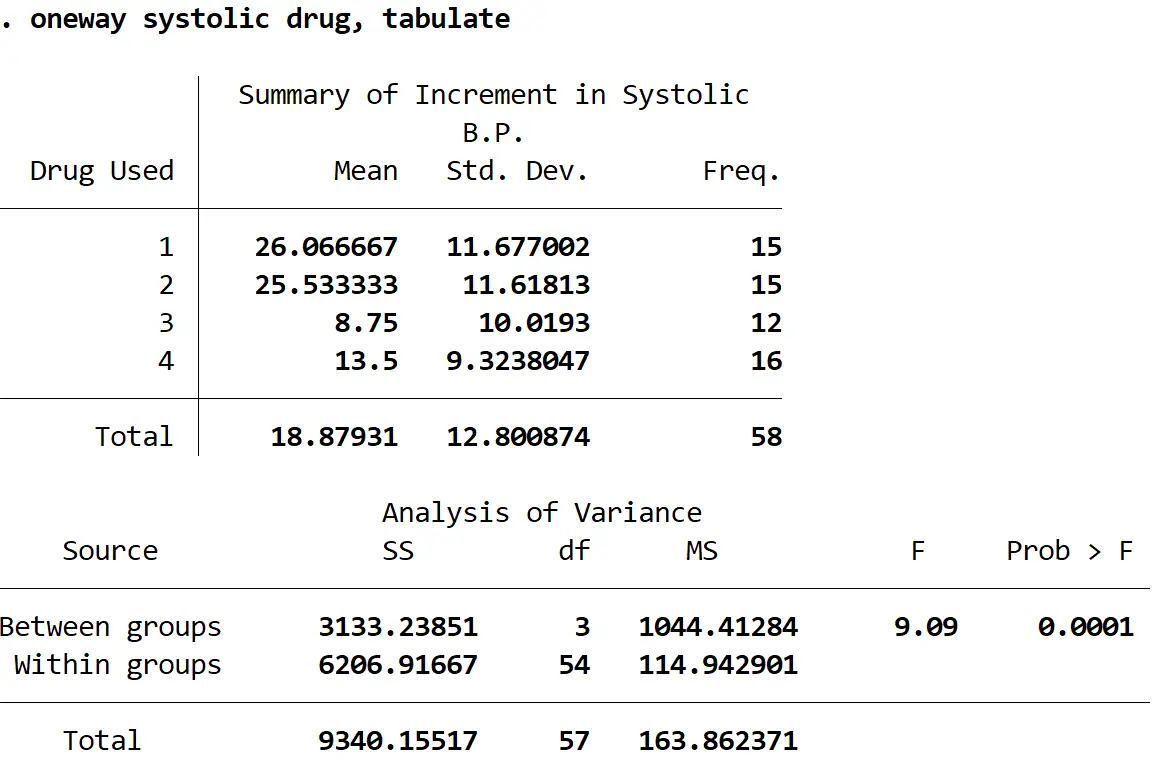
Statystyka F wynosi 9,09 , a odpowiadająca jej wartość p wynosi 0,0001 . Ponieważ wartość p jest mniejsza niż alfa = 0,05, możemy odrzucić hipotezę zerową, że średnia zmiana skurczowego ciśnienia krwi dla każdej grupy jest równa.
Innymi słowy, istnieje statystycznie istotna różnica w średniej zmianie skurczowego ciśnienia krwi pomiędzy co najmniej dwiema grupami leków.
Krok 5: Uruchom wiele testów porównawczych.
Następnie możemy przeprowadzić kilka testów porównawczych, aby faktycznie dowiedzieć się, które średnie grupowe różnią się od siebie.
Z górnego paska menu przejdź do Statystyki > Podsumowania, tabele i testy > Statystyki podsumowujące i opisowe > Porównania średnich parami .
W polu Zmienna wybierz zmienną reakcji skurczowej . W przypadku Over wybierz zmienną objaśniającą lek . W polu Korekta dla wielokrotnych porównań wybierz metodę Tukeya .
Następnie w podnagłówku Raportowanie kliknij przycisk obok Tabele efektów i zaznacz pole obok Pokaż tabelę efektów z przedziałami ufności i wartościami p . Następnie kliknij OK .
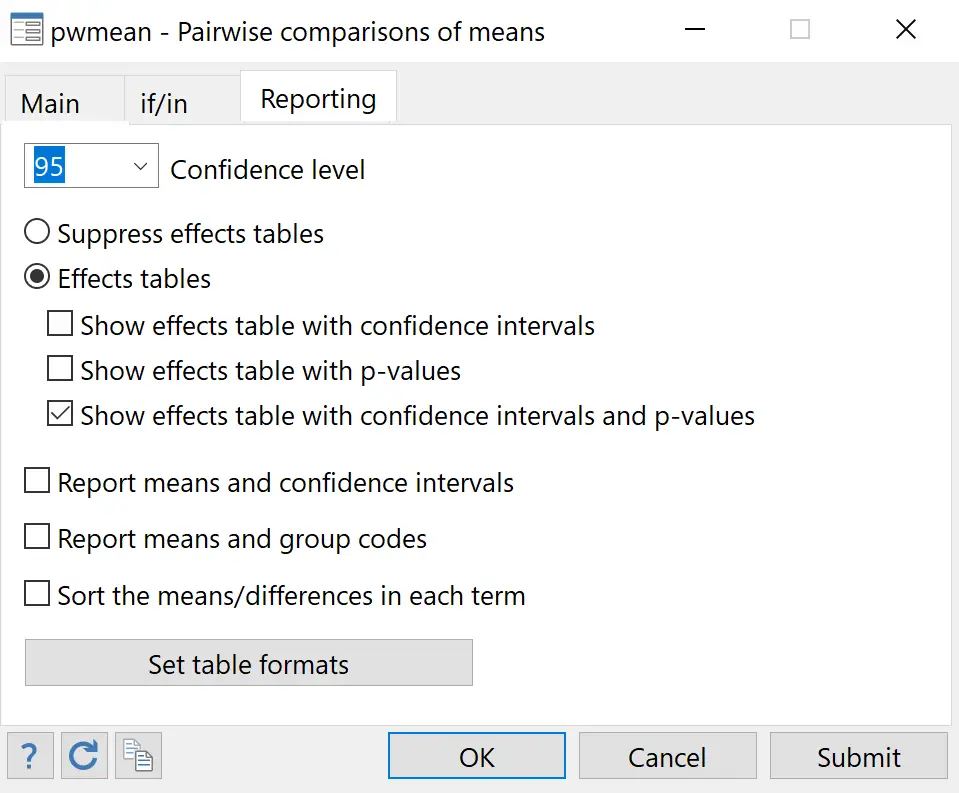
Wyświetlone zostaną następujące wyniki:
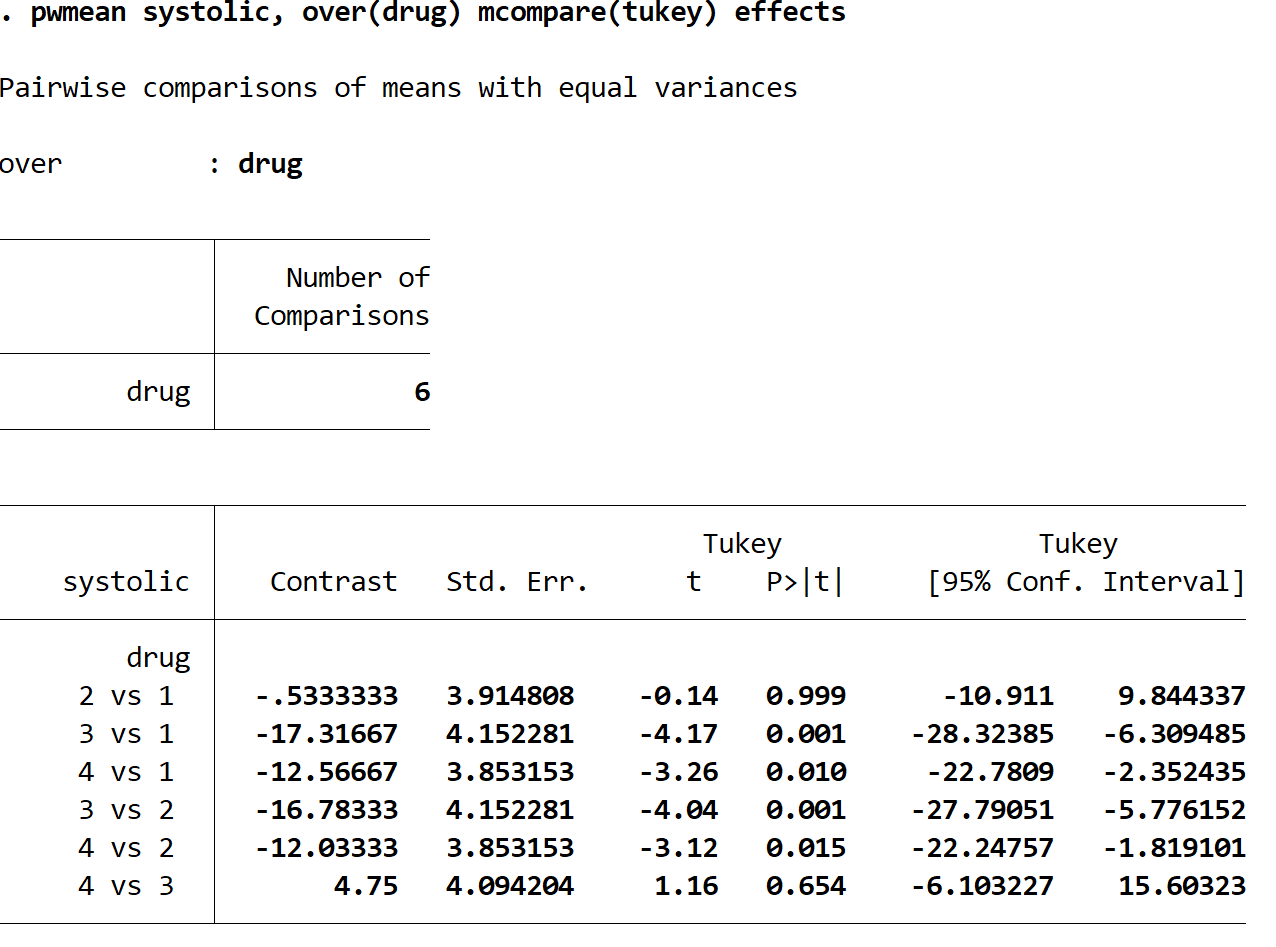
Każdy wiersz przedstawia porównanie dwóch określonych grup leków. Na przykład pierwszy wiersz porównuje średnią zmianę skurczowego ciśnienia krwi pomiędzy grupą leków 2 i grupą leków 1. Wartość p dla tego porównania wynosi 0,999 , czyli jest niezwykle wysoka i nie mniejsza niż 0,05. Oznacza to, że nie ma statystycznie istotnej różnicy pomiędzy grupami leków 1 i 2.
Widzimy jednak, że wartości p dla następujących porównań są mniejsze niż 0,05:
- lekarstwo 3 do 1 | wartość p = 0,001
- lekarstwo 4 do 1 | wartość p = 0,010
- lekarstwo 3 na 2 | wartość p = 0,001
- lekarstwo 4 na 2 | wartość p = 0,015
Oznacza to, że różnica w średniej zmianie skurczowego ciśnienia krwi jest statystycznie istotna pomiędzy każdą z tych grup.
Krok 6: Ogłoś wyniki.
Na koniec przedstawimy wyniki naszej jednokierunkowej analizy ANOVA. Oto przykład, jak to zrobić:
Przeprowadzono jednoczynnikową analizę ANOVA w celu ustalenia, czy cztery różne rodzaje leków mają różny wpływ na skurczowe ciśnienie krwi.
Poniższa tabela podsumowuje liczbę uczestników w każdej grupie, a także średnią zmianę skurczowego ciśnienia krwi i odchylenie standardowe skurczowego ciśnienia krwi dla każdej grupy:
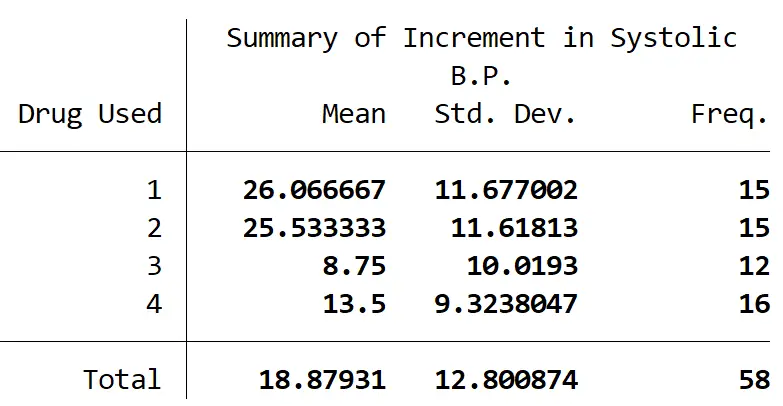
Jednoczynnikowa analiza ANOVA ujawniła, że istniała statystycznie istotna różnica pomiędzy co najmniej dwiema grupami (F(3, 54) = 9,09, p = 0,001).
Test Tukeya dla porównań wielokrotnych wykazał, że zmiana skurczowego ciśnienia krwi była statystycznie istotnie większa dla leku 3 niż dla leku 1 (17,32 +/- 4,15, p = 0,001), dla leku 3 w porównaniu z lekiem 2 (16,78 +/- 4,15, p = 0,001), dla leku 4 w porównaniu z lekiem 1 (12,57 +/- 3,85, p = 0,010), a dla leku 4 w porównaniu z lekiem 2 (12,03 +/- 3,85, p = 0,015).
Nie stwierdzono istotnej statystycznie różnicy pomiędzy grupami leków 1 i 2 (0,533 +/- 3,91, p = 0,999) ani pomiędzy grupami leków 3 i 4 (4,75 +/- 4,09, p = 0,654).