Czy wariancja może być ujemna?

W statystyce termin wariancja odnosi się do sposobu rozkładu wartości w danym zbiorze danych.

Częstym pytaniem, jakie uczniowie zadają na temat wariancji, jest:

Czy wariancja może być ujemna?

Odpowiedź: Nie, wariancja nie może być ujemna. Najniższa wartość, jaką może przyjąć, to zero.

Aby zrozumieć, dlaczego tak się dzieje, musimy zrozumieć, w jaki sposób faktycznie oblicza się wariancję.

Jak obliczyć różnicę

Wzór na znalezienie wariancji próbki (oznaczony jako s ² ) jest następujący:

s ² = Σ (x _ja – x ) ² / (n-1)

Złoto:

• x : Przykładowe środki
• x _i : ^i- ta obserwacja w próbie
• N : Rozmiar próbki
• Σ : grecki symbol oznaczający „sumę”

Załóżmy na przykład, że mamy następujący zbiór danych zawierający 10 wartości:

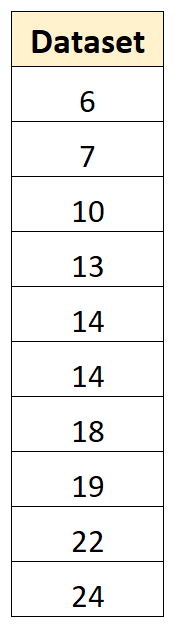
Aby obliczyć wariancję tej próbki, możemy wykonać następujące kroki:

Krok 1: Znajdź średnią

Średnia to po prostu średnia. Okazuje się, że jest to 14,7 .

Krok 2: Znajdź kwadraty odchyleń

Następnie możemy obliczyć odchylenie kwadratowe każdej indywidualnej wartości od średniej.

Na przykład pierwsze odchylenie kwadratowe oblicza się jako (6-14,7) ² = 75,69.

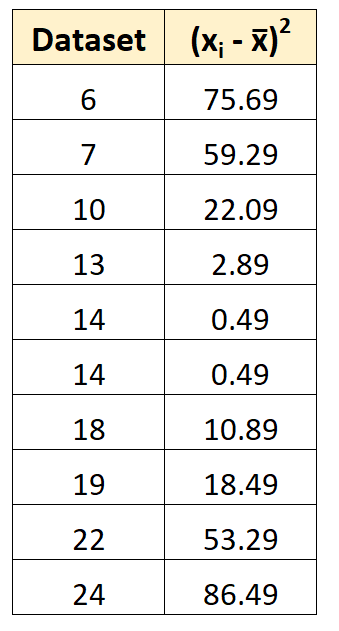
Krok 3: Znajdź sumę kwadratów odchyleń

Następnie możemy zsumować wszystkie kwadraty odchyleń:

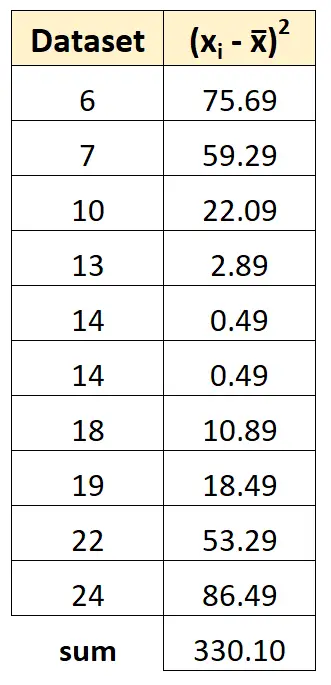
Krok 4: Oblicz wariancję próbki

Na koniec możemy obliczyć wariancję próbki jako sumę kwadratów odchyleń podzieloną przez (n-1):

s ² = 330,1 / (10-1) = 330,1 / 9 = 36,678

Wariancja próbki wynosi 36 678 .

Przykład zerowej wariancji

Jedynym sposobem, aby zbiór danych miał zerową wariancję, jest sytuacja, gdy wszystkie wartości w zbiorze danych są takie same .

Na przykład następujący zestaw danych ma wariancję próbki równą zero:

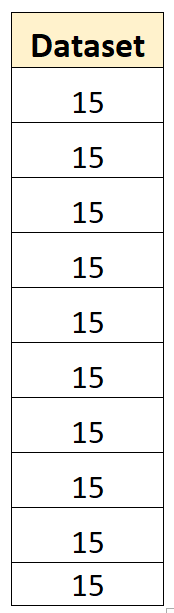
Średnia zbioru danych wynosi 15 i żadna z poszczególnych wartości nie odbiega od średniej. Zatem suma kwadratów odchyleń będzie wynosić zero, a wariancja próbki będzie po prostu wynosić zero.

Czy odchylenie standardowe może być ujemne?

Bardziej powszechnym sposobem pomiaru rozkładu wartości w zbiorze danych jest użycie odchylenia standardowego, które jest po prostu pierwiastkiem kwadratowym z wariancji.

Przykładowo, jeśli wariancja danej próbki wynosi ^s2 = 36,678 , to odchylenie standardowe (zapisane s ) oblicza się w następujący sposób:

s = √ ^s2 = √ 36,678 = 6,056

Ponieważ wiemy już, że wariancja wynosi zawsze zero lub liczbę dodatnią, oznacza to, że odchylenie standardowe nigdy nie może być ujemne, ponieważ pierwiastek kwadratowy z zera lub liczby dodatniej nie może być ujemny.

Dodatkowe zasoby

Miary tendencji centralnej: definicja i przykłady
Miary dyspersji: definicja i przykłady