Jaka jest pozostała luka? (definicja – przykład)

Wariancja resztowa (czasami nazywana „niewyjaśnioną wariancją”) odnosi się do wariancji w modelu, której nie można wyjaśnić zmiennymi modelu.

Im wyższa wariancja resztowa modelu, tym mniej model jest w stanie wyjaśnić zmienność danych.

Wariancja resztowa pojawia się w wynikach dwóch różnych modeli statystycznych:

1. ANOVA: stosowana do porównania średnich z trzech lub więcej niezależnych grup.

2. Regresja: stosowana do ilościowego określenia związku pomiędzy jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Poniższe przykłady pokazują, jak interpretować wariancję resztową w każdej z tych metod.

Wariancja resztowa w modelach ANOVA

Za każdym razem, gdy dopasowujemy model ANOVA („analiza wariancji”), otrzymujemy tabelę ANOVA, która wygląda następująco:

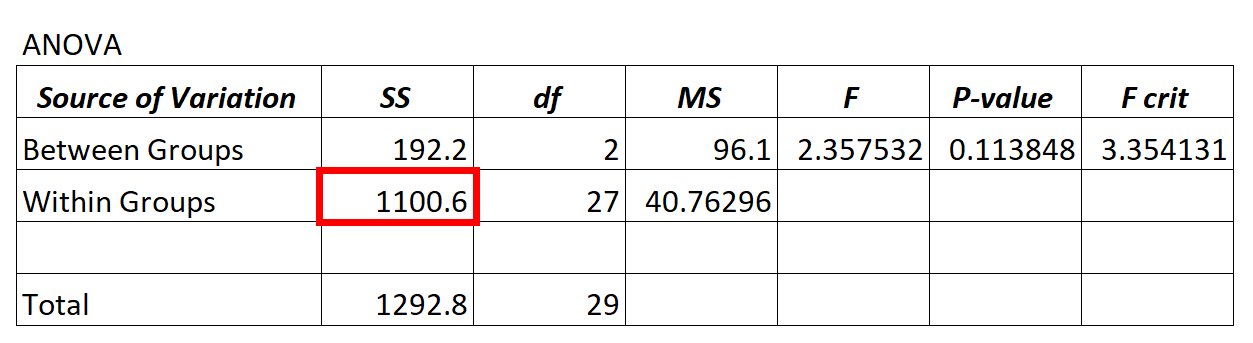
Wartość wariancji resztowej z modelu ANOVA znajduje się w kolumnie SS („suma kwadratów”) dla zmienności wewnątrzgrupowej .

Wartość ta nazywana jest także „sumą kwadratów błędów” i jest obliczana przy użyciu następującego wzoru:

Σ(X _ij – X _j ) ²

Złoto:

• Σ : grecki symbol oznaczający „sumę”
• X _ij : ^i-ta obserwacja grupy j
• X _j : średnia grupy j

W powyższym modelu ANOVA widzimy, że wariancja resztowa wynosi 1100,6.

Aby określić, czy ta wariancja resztowa jest „wysoka”, możemy obliczyć średnią sumę kwadratów dla grup i średnią sumę kwadratów pomiędzy grupami i znaleźć stosunek między nimi, co daje ogólną wartość F w tabeli ANOVA.

• F = MS _wchodzi / MS _wchodzi
• F = 96,1 / 40,76296
• F = 2,357

Wartość F w powyższej tabeli ANOVA wynosi 2,357, a odpowiadająca jej wartość p wynosi 0,113848. Ponieważ ta wartość p jest nie mniejsza niż α = 0,05, nie mamy wystarczających dowodów, aby odrzucić hipotezę zerową.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że średnia różnica między porównywanymi grupami jest znacząco różna.

Mówi nam to, że wariancja resztowa modelu ANOVA jest wysoka w porównaniu ze wariancją, którą model może faktycznie wyjaśnić.

Wariancja resztowa w modelach regresji

W modelu regresji wariancję resztową definiuje się jako sumę kwadratów różnic między przewidywanymi punktami danych i obserwowanymi punktami danych.

Oblicza się go w następujący sposób:

Σ(ŷ _i – y _i ) ²

Złoto:

• Σ : grecki symbol oznaczający „sumę”
• ŷ _i : Przewidywane punkty danych
• y _i : Obserwowane punkty danych

Kiedy dopasowujemy model regresji, zwykle otrzymujemy wynik wyglądający następująco:

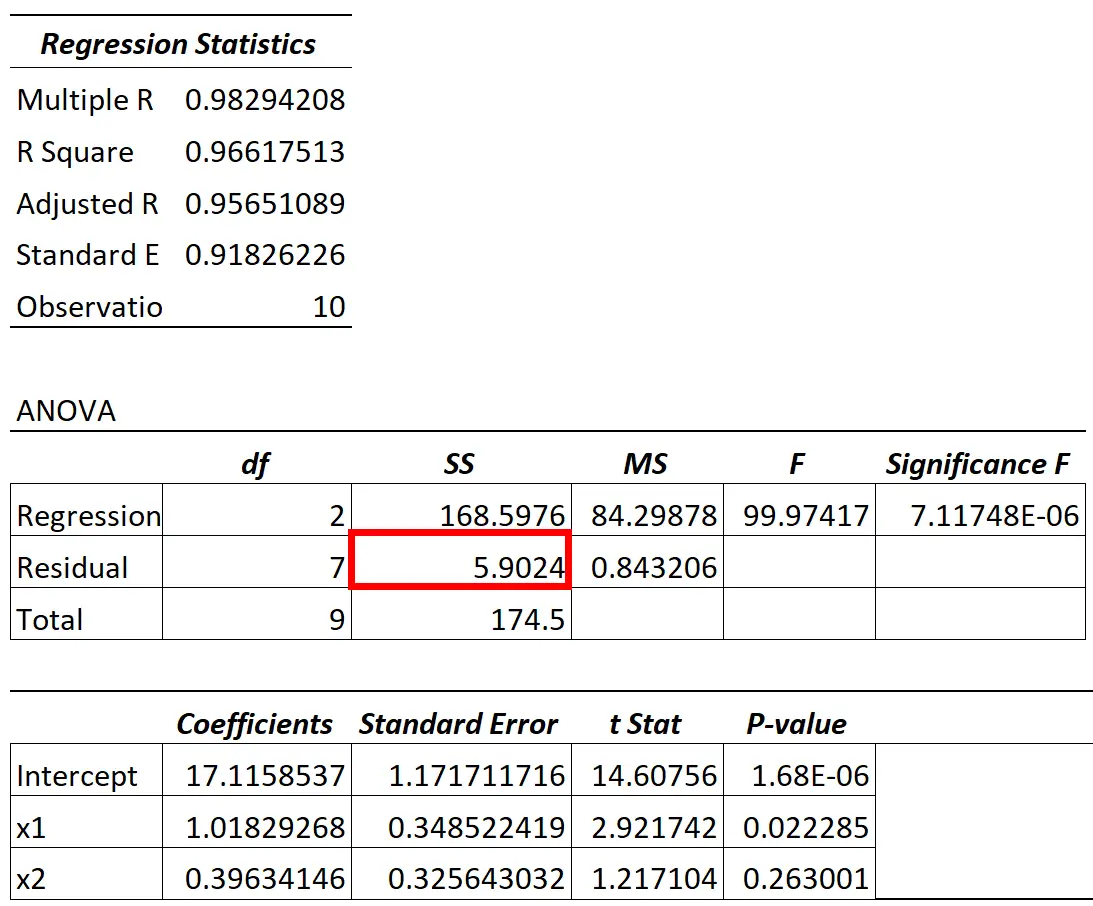
Wartość wariancji resztowej z modelu ANOVA można znaleźć w kolumnie SS („suma kwadratów”) dla wariancji resztowej.

Stosunek zmienności resztowej do zmienności całkowitej w modelu mówi nam, jaki procent zmienności zmiennej odpowiedzi nie może być wyjaśniony przez zmienne predykcyjne w modelu.

Na przykład w powyższej tabeli obliczylibyśmy ten procent w następujący sposób:

• Niewyjaśniona zmienność = pozostałość SS / suma SS
• Niewyjaśniona zmienność = 5,9024 / 174,5
• Niewyjaśniona zmienność = 0,0338

Wartość tę można również obliczyć za pomocą następującego wzoru:

• Niewyjaśniona zmienność = 1 – R ²
• Niewyjaśniona zmienność = 1 – 0,96617
• Niewyjaśniona zmienność = 0,0338

Wartość R-kwadrat modelu mówi nam, jaki procent zmienności zmiennej odpowiedzi można wyjaśnić za pomocą zmiennej predykcyjnej.

Zatem im mniejsza jest niewyjaśniona zmienność, tym łatwiej model może wykorzystać zmienne predykcyjne do wyjaśnienia zmienności zmiennej odpowiedzi.

Dodatkowe zasoby

Jaka jest dobra wartość R-kwadrat?
Jak obliczyć R-kwadrat w Excelu
Jak obliczyć R-kwadrat w R