Jak znaleźć wariancję zgrupowanych danych (z przykładem)

Często chcemy obliczyć wariancję zgrupowanego rozkładu częstotliwości.

Załóżmy na przykład, że mamy następujący zgrupowany rozkład częstotliwości:

Chociaż nie jest możliwe obliczenie dokładnej wariancji, ponieważ nie znamy wartości danych surowych , możliwe jest oszacowanie wariancji za pomocą następującego wzoru:

Wariancja: Σn _i (m _i -μ) ² / (N-1)

Złoto:

• n _i : Częstotliwość i- ^tej grupy
• _mi : Środek i- ^tej grupy
• µ : Średnia
• N: Całkowity rozmiar próbki

Uwaga: Środek każdej grupy można znaleźć, biorąc średnią z dolnej i górnej wartości zakresu. Na przykład punkt środkowy pierwszej grupy oblicza się w następujący sposób: (1+10) / 2 = 5,5.

Poniższy przykład pokazuje, jak zastosować tę formułę w praktyce.

Przykład: Oblicz wariancję pogrupowanych danych

Załóżmy, że mamy następujące pogrupowane dane:

Oto jak użylibyśmy wspomnianego wcześniej wzoru do obliczenia wariancji tych pogrupowanych danych:

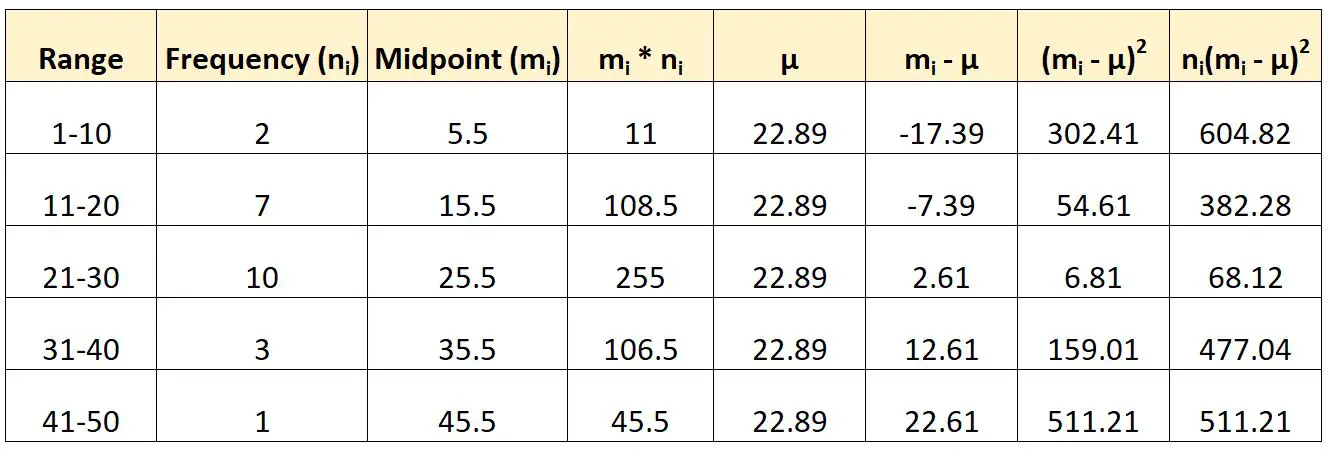
Następnie obliczylibyśmy wariancję w następujący sposób:

• Wariancja: Σn _i (m _i -μ) ² / (N-1)
• Różnica : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Różnica : 92,885

Wariancja zbioru danych wynosi 92,885 .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak obliczać inne metryki dla pogrupowanych danych:

Jak znaleźć średnią i odchylenie standardowe pogrupowanych danych
Jak obliczyć ranking percentylowy dla pogrupowanych danych
Jak znaleźć medianę pogrupowanych danych
Jak znaleźć tryb pogrupowanych danych