Jak obliczyć oczekiwaną wartość x^2
W przypadku zmiennej losowej oznaczonej X można zastosować następujący wzór do obliczenia oczekiwanej wartości X 2 :
E(X 2 ) = Σx 2 * p(x)
Złoto:
- Σ : Symbol oznaczający „sumę”
- x : Wartość zmiennej losowej
- p(x) : Prawdopodobieństwo, że zmienna losowa przyjmie daną wartość
Poniższy przykład pokazuje, jak zastosować tę formułę w praktyce.
Przykład: Obliczenie oczekiwanej wartości X 2
Załóżmy, że mamy następującą tabelę rozkładu prawdopodobieństwa, która opisuje prawdopodobieństwo, że zmienna losowa,
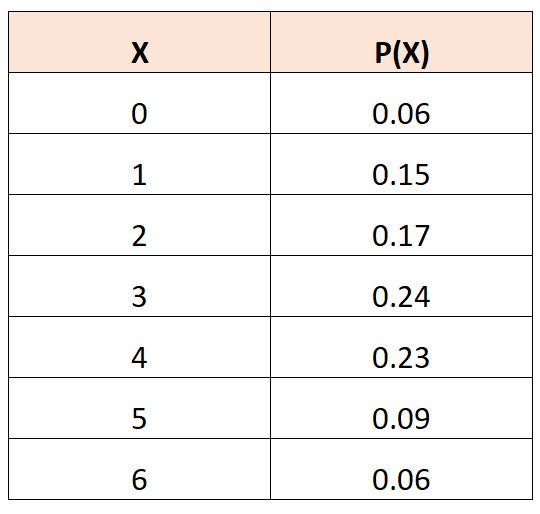
Aby obliczyć oczekiwaną wartość X 2 , możemy skorzystać z następującego wzoru:
E(X 2 ) = Σx 2 * p(x)
E(X 2 ) = (0) 2 *.06 + (1) 2 *.15 + (2) 2 *.17 + (3) 2 *.24 + (4) 2 *.23 + (5) 2 *.09 + (6) 2 *.06
E( X2 ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16
E( X2 ) = 11,08
Oczekiwana wartość X 2 wynosi 11,08 .
Należy zauważyć, że ta zmienna losowa jest dyskretną zmienną losową , co oznacza, że może przyjmować tylko skończoną liczbę wartości.
Jeżeli X jest ciągłą zmienną losową , musimy zastosować następujący wzór do obliczenia oczekiwanej wartości X2 :
E(X 2 ) = ∫ x 2 f(x)dx
Złoto:
- ∫: Symbol oznaczający „integrację”
- f(x) : Plik PDF jest kontynuowany dla zmiennej losowej
Obliczając oczekiwaną wartość X2 dla ciągłej zmiennej losowej, zazwyczaj korzystamy z oprogramowania statystycznego, ponieważ ręczne wykonanie tego obliczenia może być trudniejsze.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w statystykach:
Jak znaleźć średnią rozkładu prawdopodobieństwa
Jak znaleźć odchylenie standardowe rozkładu prawdopodobieństwa
Jak znaleźć wariancję rozkładu prawdopodobieństwa