Jak znaleźć wartość p na podstawie wyniku t w programie excel

Często w statystykach test hipotezy skutkuje statystyką testu T-score. Kiedy już znajdziemy ten wynik t, zazwyczaj znajdujemy powiązaną z nim wartość p. Jeśli ta wartość p jest poniżej pewnego poziomu alfa (np. 0,10, 0,05, 0,01), wówczas odrzucamy hipotezę zerową testu i stwierdzamy, że nasze wyniki są istotne.

W tym samouczku wyjaśniono, jak znaleźć wartość p na podstawie wyniku t w programie Excel za pomocą funkcji ROZKŁAD T , która przyjmuje następujące argumenty:

ROZKŁ.T (x, stopień_swobody)

Złoto:

• x: Wynik T, który nas interesuje.
• deg_freedom: Stopnie swobody.

Zobaczmy kilka przykładów.

Przykład 1: Wartość P na podstawie wyniku t (dwustronna)

Botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. W losowej próbie 12 roślin stwierdziła, że średnia wysokość próbki wynosi 14,33 cala, a odchylenie standardowe próbki wynosi 1,37 cala.

Wykonaj dwustronny test hipotezy, używając poziomu alfa 0,05, aby określić, czy średnia wysokość wynosi 15 cali.

Krok 1: Postaw hipotezy.

Hipoteza zerowa (H ₀ ): μ = 15

Hipoteza alternatywna: (Ha): μ ≠ 15

Krok 2: Znajdź wartość T i stopnie swobody.

wynik t = ( x -μ) / (s/√n) = (14,33-15) / (1,37/√12) = -1,694 .

stopnie swobody = n-1 = 12-1 = 11 .

Krok 3: Znajdź wartość p wyniku t za pomocą programu Excel.

Aby znaleźć wartość p wyniku t, użyjemy następującej formuły w Excelu:

=T.ROZKŁ.2T(ABS(-1,694); 11)

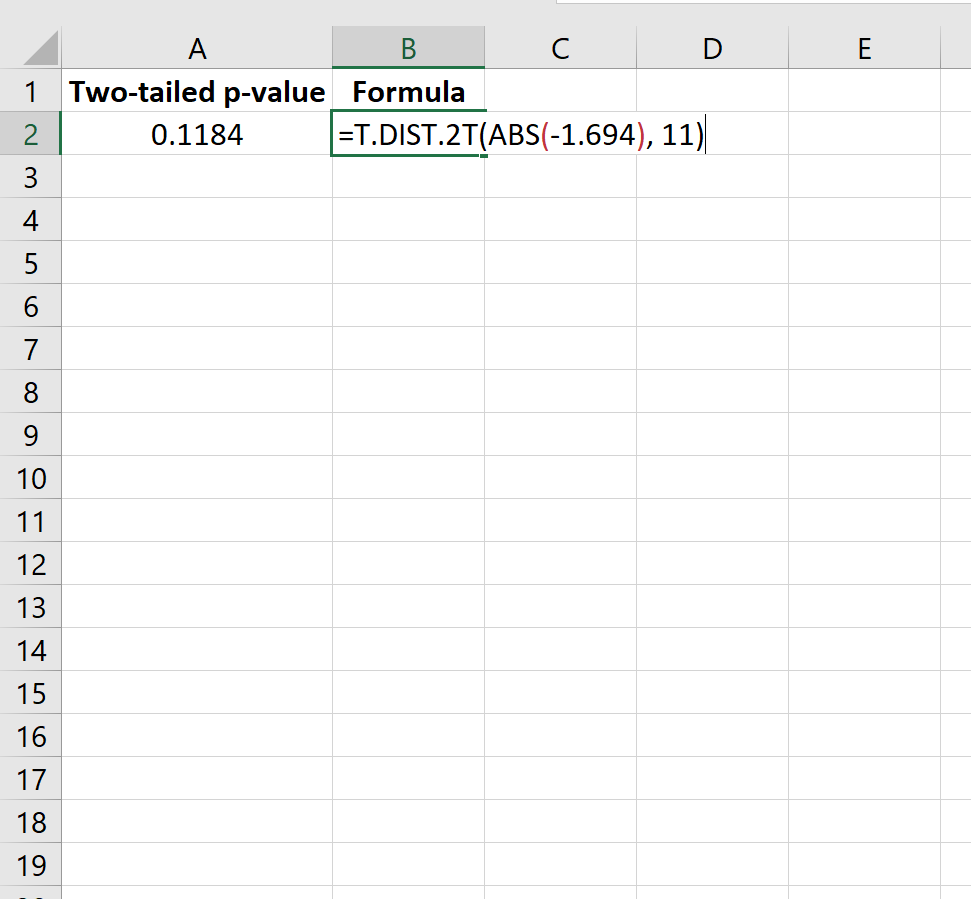
To mówi nam, że dwustronna wartość p wynosi 0,1184 .

Krok 4: Odrzuć lub nie odrzucaj hipotezy zerowej.

Ponieważ wartość p wynosząca 0,1184 jest nie mniejsza niż wybrany poziom alfa wynoszący 0,05 , nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość rośliny różni się od 15 cali.

Przykład 2: Wartość P z wyniku T (jednostronna)

Firma chce wiedzieć, czy nowy typ baterii ma dłuższą średnią żywotność niż obecna standardowa bateria, która ma średnią żywotność 18 godzin. W losowej próbie 25 nowych baterii stwierdzono, że średnia żywotność wynosi 19 godzin przy odchyleniu standardowym wynoszącym 4 godziny.

Wykonaj jednostronny test hipotezy, stosując poziom alfa 0,05, aby określić, czy średnia żywotność nowej baterii jest dłuższa niż średnia żywotność obecnej baterii standardowej.

Krok 1: Postaw hipotezy.

Hipoteza zerowa (H ₀ ): μ ≤ 18

Hipoteza alternatywna: (Ha): μ > 18

Krok 2: Znajdź wartość T i stopnie swobody.

wynik t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .

stopnie swobody = n-1 = 25-1 = 24 .

Krok 3: Znajdź wartość p wyniku t za pomocą programu Excel.

Aby znaleźć wartość p wyniku t, użyjemy następującej formuły w Excelu:

= ROZKŁAD.T.RT(1,25; 24)

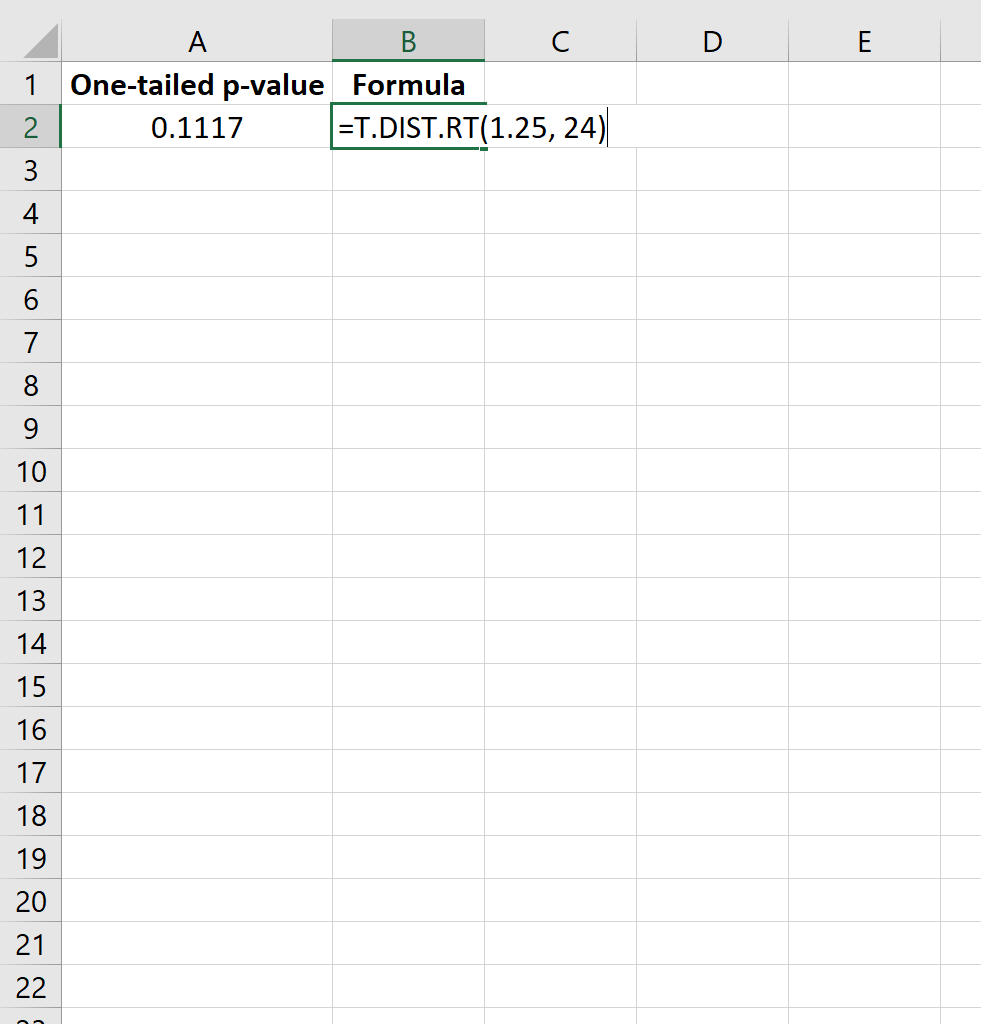
To mówi nam, że jednostronna wartość p wynosi 0,1117 .

Krok 4: Odrzuć lub nie odrzucaj hipotezy zerowej.

Ponieważ wartość p wynosząca 0,1117 jest większa niż wybrany poziom alfa wynoszący 0,05 , nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia żywotność nowego akumulatora jest dłuższa niż średnia żywotność obecnego standardowego akumulatora.

Aby uzyskać więcej samouczków na temat statystyk w programie Excel, zapoznaj się z naszą pełną listą przewodników po programie Excel .