Różnica między wartościami z i wartościami p w statystykach

Dwa terminy, które uczniowie często mylą w statystykach, to wartości z i wartości p .

Aby zrozumieć różnicę między tymi terminami, pomocne jest zrozumienie testów z .

Istnieją dwa popularne typy testów Z:

• Test z jednej próby : używany do sprawdzenia, czy średnia populacji jest równa określonej wartości.
• Test z dwóch prób : używany do sprawdzania, czy średnie z dwóch populacji są równe.

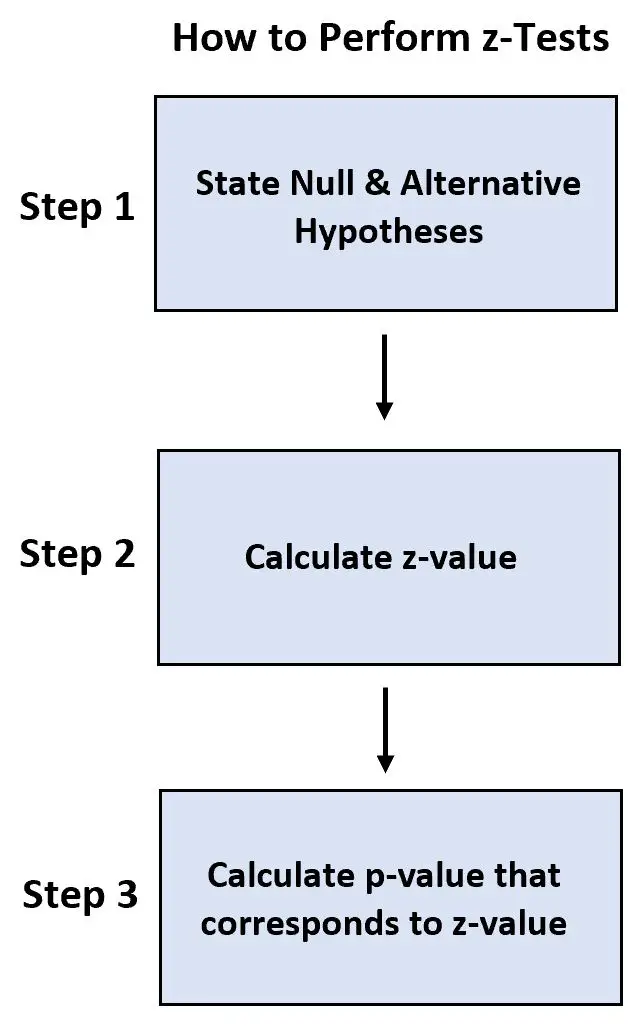
Aby wykonać każdy test, wykonujemy następujące kroki:

• Krok 1: Podaj hipotezę zerową i alternatywną.
• Krok 2: Oblicz wartość z.
• Krok 3: Oblicz wartość p odpowiadającą wartości z.

W przypadku każdego testu wartość z jest sposobem ilościowego określenia różnicy między średnimi populacji, a wartość p oznacza prawdopodobieństwo otrzymania wartości z o wartości bezwzględnej co najmniej tak dużej, jak faktycznie zaobserwowaliśmy w „próbce”. danych, jeśli hipoteza zerowa jest rzeczywiście prawdziwa.

Jeśli wartość p jest mniejsza od określonej wartości (np. 0,05), wówczas odrzucamy hipotezę zerową testu.

Dla każdego typu testu z interesuje nas wartość p i po prostu używamy wartości z jako etapu pośredniego do obliczenia wartości p.

Poniższy przykład pokazuje, jak obliczyć i zinterpretować wartość z i odpowiadającą jej wartość p dla testu z dwóch próbek.

Przykład: Oblicz i zinterpretuj wartości Z i wartości P

Załóżmy, że poziomy IQ osób z dwóch różnych miast mają rozkład normalny, a każde z nich ma odchylenia standardowe populacji wynoszące 15.

Naukowiec chce wiedzieć, czy średni poziom IQ pomiędzy mieszkańcami miasta A i B jest inny. Dlatego wybiera prostą losową próbę 20 osób z każdego miasta i rejestruje ich poziom IQ:

Miasto A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Miasto B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

Oto jak przeprowadzić test Z dla dwóch próbek, korzystając z tych danych:

Krok 1: Podaj hipotezę zerową i alternatywną.

Najpierw przedstawimy hipotezę zerową i alternatywną:

• H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)
• H ₁ : μ ₁ ≠ μ ₂ (średnie z obu populacji nie są równe)

Krok 2: Oblicz wartość z.

Następnie przeprowadzimy w programie Excel test z dwóch próbek, korzystając z tych danych i ustalimy, że wartość z wynosi -1,71817 .

Krok 3: Oblicz wartość p.

Możemy użyć kalkulatora wartości Z do P, aby stwierdzić, że wartość p odpowiadająca wartości az wynoszącej -1,71817 wynosi 0,08577.

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie mamy wystarczających dowodów, aby odrzucić hipotezę zerową.

Wnioskujemy zatem, że średni poziom IQ nie różni się istotnie pomiędzy obydwoma miastami.

Należy zauważyć, że po prostu użyliśmy wartości z jako etapu pośredniego do obliczenia wartości p.

Wartość p to prawdziwa wartość, która nas interesowała, ale najpierw musieliśmy obliczyć wartość z.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak przeprowadzać testy Z przy użyciu różnych programów statystycznych:

Jak wykonać testy Z w programie Excel
Jak wykonać testy Z w R
Jak wykonać testy Z w Pythonie