Czy na rozstęp międzykwartylowy (iqr) wpływają wartości odstające?
W statystykach często chcemy wiedzieć, jak szeroko wartości są „rozłożone” w rozkładzie.
Popularną metodą pomiaru rozrzutu jest rozstęp międzykwartylowy , który oblicza się jako różnicę między pierwszym a trzecim kwartylem zbioru danych. Kwartyle to po prostu wartości dzielące zbiór danych na cztery równe części.
Przykład: Obliczanie rozstępu międzykwartylowego
Poniższy przykład pokazuje, jak obliczyć rozstęp międzykwartylowy dla danego zbioru danych:
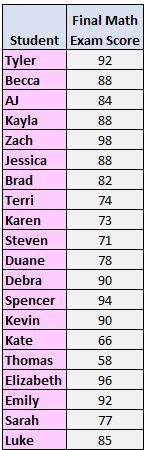
Krok 1: Ułóż wartości od najmniejszej do największej.
58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
2. Znajdź medianę.
58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
W tym przypadku mediana wynosi od 85 do 88.
3. Mediana dzieli zbiór danych na dwie połowy. Mediana dolnej połowy to dolny kwartyl, a mediana górnej połowy to górny kwartyl:
58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98
4. Oblicz rozstęp międzykwartylowy.
W tym przypadku pierwszy kwartyl to średnia dwóch środkowych wartości w dolnej połowie zbioru danych (75,5), a trzeci kwartyl to średnia dwóch środkowych wartości w górnej połowie zbioru danych (91).
Zatem rozstęp międzykwartylowy wynosi 91 – 75,5 = 15,5
Wartości odstające nie mają wpływu na rozstęp międzykwartylowy
Jednym z powodów, dla których ludzie wolą używać rozstępu międzykwartylowego (IQR) przy obliczaniu „rozrzutu” zbioru danych, jest jego odporność na wartości odstające. Ponieważ IQR to po prostu środkowy zakres 50% wartości danych, skrajne wartości odstające nie mają na niego wpływu.
Aby to zademonstrować, rozważ następujący zbiór danych:
[1, 4, 8, 11, 13, 17, 17, 20]
Oto różne metryki propagacji dla tego zbioru danych:
- Rozstęp międzykwartylowy: 11
- Zasięg: 19
- Odchylenie standardowe: 6,26
- Różnica: 39,23
Rozważmy teraz ten sam zestaw danych, ale z dodaną skrajną wartością odstającą:
[1, 4, 8, 11, 13, 17, 17, 20, 150 ]
Oto różne metryki propagacji dla tego zbioru danych:
- Rozstęp międzykwartylowy: 12,5
- Zasięg: 149
- Odchylenie standardowe: 43,96
- Rozpiętość: 1932,84
Zwróć uwagę, że rozstęp międzykwartylowy zmienia się tylko nieznacznie, z 11 do 12,5. Jednakże wszystkie inne miary rozproszenia zmieniają się dramatycznie.
Pokazuje to, że na rozstęp międzykwartylowy nie mają wpływu wartości odstające, podobnie jak inne miary rozproszenia. Z tego powodu jest to niezawodny sposób pomiaru rozkładu środkowych 50% wartości w dowolnym rozkładzie.
Dalsza lektura:
Pomiary dyspersji
Kalkulator rozstępu międzykwartylowego