Jak wykonać ważoną regresję metodą najmniejszych kwadratów w r

Jednym z kluczowych założeń regresji liniowej jest to, że reszty mają rozkład z równą wariancją na każdym poziomie zmiennej predykcyjnej. Założenie to znane jest jako homoskedastyczność .

Jeżeli to założenie nie jest przestrzegane, w resztach występuje heteroskedastyczność . Kiedy tak się dzieje, wyniki regresji stają się niewiarygodne.

Jednym ze sposobów rozwiązania tego problemu jest zastosowanie regresji ważonej metodą najmniejszych kwadratów , która przypisuje wagi obserwacjom w taki sposób, że obserwacje o małej wariancji błędu otrzymują większą wagę, ponieważ zawierają więcej informacji w porównaniu z obserwacjami o większej wariancji błędu.

W tym samouczku przedstawiono krok po kroku przykład wykonania ważonej regresji metodą najmniejszych kwadratów w języku R.

Krok 1: Utwórz dane

Poniższy kod tworzy ramkę danych zawierającą liczbę przepracowanych godzin i odpowiadający im wynik egzaminu dla 16 uczniów:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Krok 2: Wykonaj regresję liniową

Następnie użyjemy funkcji lm(), aby dopasować prosty model regresji liniowej , który wykorzystuje godziny jako zmienną predykcyjną i wynik jakozmienną odpowiedzi :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Krok 3: Test na heteroskedastyczność

Następnie utworzymy wykres reszt i dopasowanych wartości, aby wizualnie sprawdzić heteroskedastyczność:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

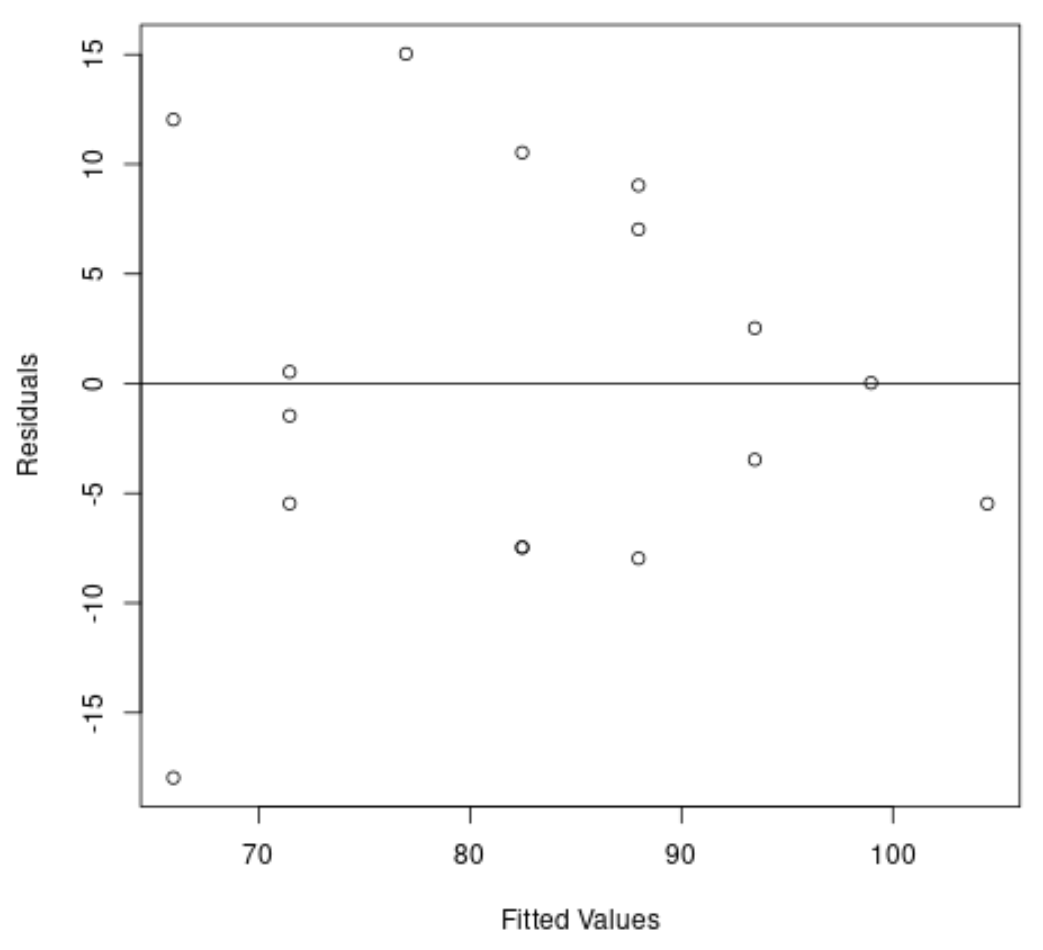
Z wykresu widzimy, że reszty mają kształt „stożka”: nie są rozmieszczone z równą wariancją na całym wykresie.

Aby formalnie przetestować heteroskedastyczność, możemy wykonać test Breuscha-Pagana:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Test Breuscha-Pagana wykorzystuje następujące hipotezy zerowe i alternatywne :

• Hipoteza zerowa (H ₀ ): występuje homoskedastyczność (reszty rozkładają się z równą wariancją)
• Hipoteza alternatywna ( _HA ): występuje heteroskedastyczność (reszty nie są rozłożone z równą wariancją)

Ponieważ wartość p testu wynosi 0,0466 , odrzucimy hipotezę zerową i dojdziemy do wniosku, że heteroskedastyczność jest problemem w tym modelu.

Krok 4: Wykonaj regresję ważoną metodą najmniejszych kwadratów

Ponieważ występuje heteroskedastyczność, przeprowadzimy ważoną metodę najmniejszych kwadratów, ustawiając wagi w taki sposób, aby obserwacje o mniejszej wariancji otrzymały większą wagę:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

Na podstawie wyników widać, że estymacja współczynnika dla zmiennej predykcyjnej godzin uległa niewielkiej zmianie, a ogólne dopasowanie modelu uległo poprawie.

Ważony model najmniejszych kwadratów ma resztkowy błąd standardowy wynoszący 1,199 w porównaniu z 9,224 w oryginalnym prostym modelu regresji liniowej.

Oznacza to, że wartości przewidywane uzyskane za pomocą modelu ważonego najmniejszych kwadratów są znacznie bliższe faktycznym obserwacjom w porównaniu z wartościami przewidywanymi uzyskanymi za pomocą prostego modelu regresji liniowej.

Ważony model najmniejszych kwadratów również ma R-kwadrat wynoszący 0,6762 w porównaniu z 0,6296 w oryginalnym prostym modelu regresji liniowej.

Oznacza to, że ważony model najmniejszych kwadratów jest w stanie wyjaśnić więcej wariancji w wynikach egzaminów niż prosty model regresji liniowej.

Pomiary te wskazują, że ważony model najmniejszych kwadratów zapewnia lepsze dopasowanie do danych w porównaniu z prostym modelem regresji liniowej.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak przeprowadzić regresję kwantylową w R