Jak wykonać test t welcha w programie excel

Najczęstszym sposobem porównania średnich między dwiema niezależnymi grupami jest użycie testu t dla dwóch prób . Jednakże w tym teście założono, że wariancje pomiędzy obiema grupami są równe.

Jeśli uważasz, że wariancja między dwiema grupami nie jest równa, możesz użyć testu t Welcha , który jest nieparametrycznym odpowiednikiem testu t dla dwóch prób.

W tym samouczku wyjaśniono, jak wykonać test t Welcha w programie Excel.

Przykład: test t Welcha w programie Excel

W tym przykładzie porównamy wyniki 12 uczniów, którzy korzystali z broszury przygotowującej do egzaminu w celu przygotowania się do egzaminu, z 12 uczniami, którzy tego nie robili.

Wykonaj poniższe kroki, aby wykonać test t Welcha w celu ustalenia, czy istnieje różnica w średnich wynikach egzaminów pomiędzy obiema grupami.

Krok 1: Wprowadź dane.

Najpierw wpisz wyniki egzaminu w dwóch kolumnach:

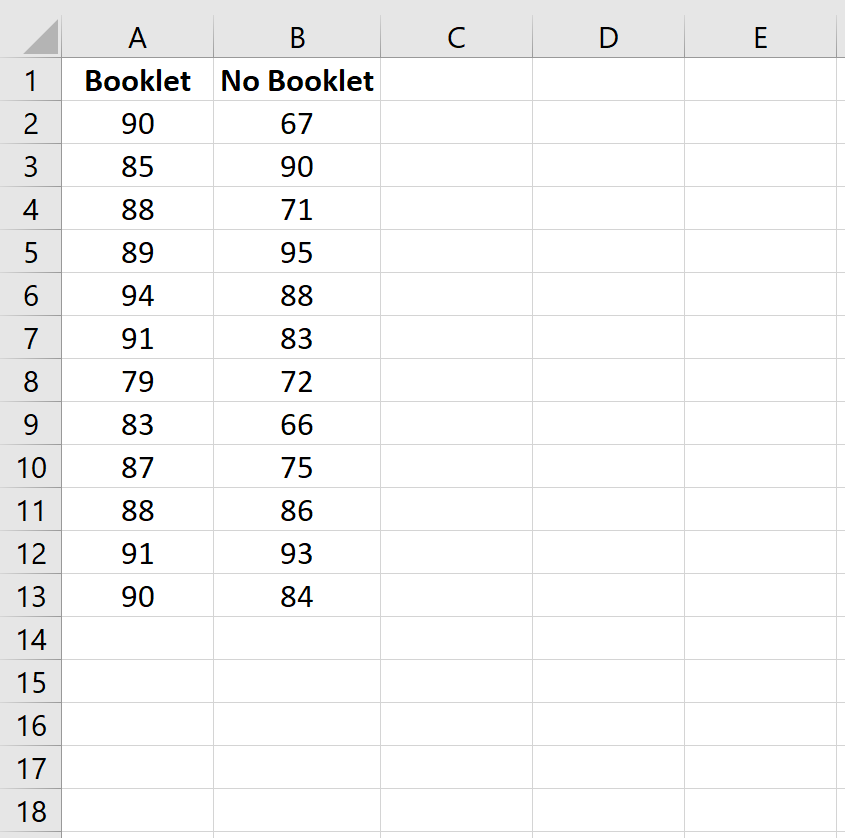
Krok 2: Wykonaj test t Welcha.

Na górnej wstążce programu Excel przejdź do karty Dane i kliknij opcję Analiza danych . Jeśli nie widzisz tej opcji, musisz najpierw zainstalować bezpłatne oprogramowanie Analysis ToolPak .

Po kliknięciu Analiza danych pojawi się nowe okno. Wybierz test t: dwie próbki przy założeniu nierównych wariancji i kliknij OK .

W nowym oknie wprowadź zakres wartości danych dla Zmiennej 1 i Zmiennej 2 wraz z ich etykietami grupowymi. W polu Hipotetyczna średnia różnica wpisz 0. Zaznacz pole obok Etykiety . Pozostaw Alpha ustawioną na 0,05. W polu Zakres wyjściowy wybierz komórkę, w której mają się pojawić wyniki testu. Następnie kliknij OK .

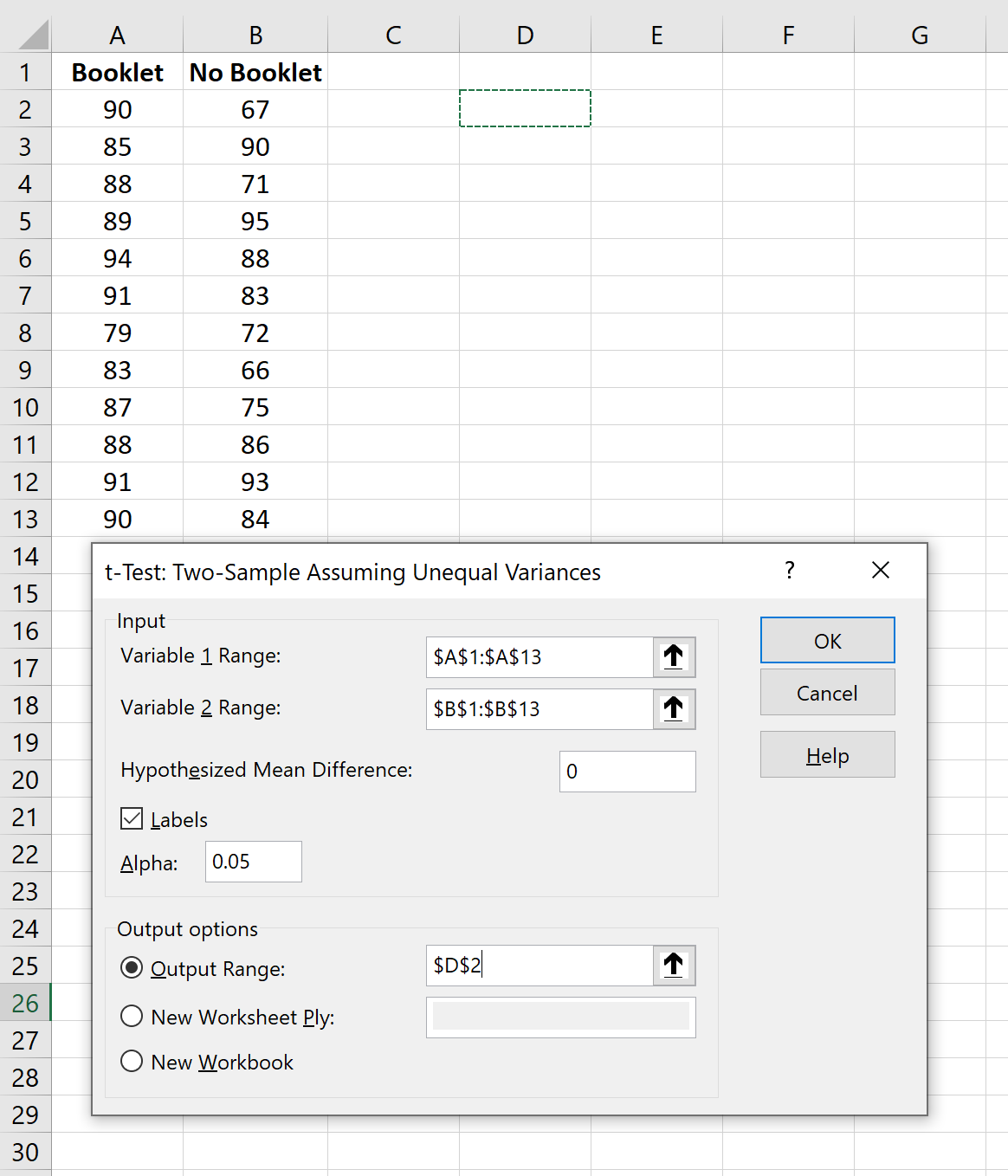
Następujące dane wyjściowe pojawiają się automatycznie:

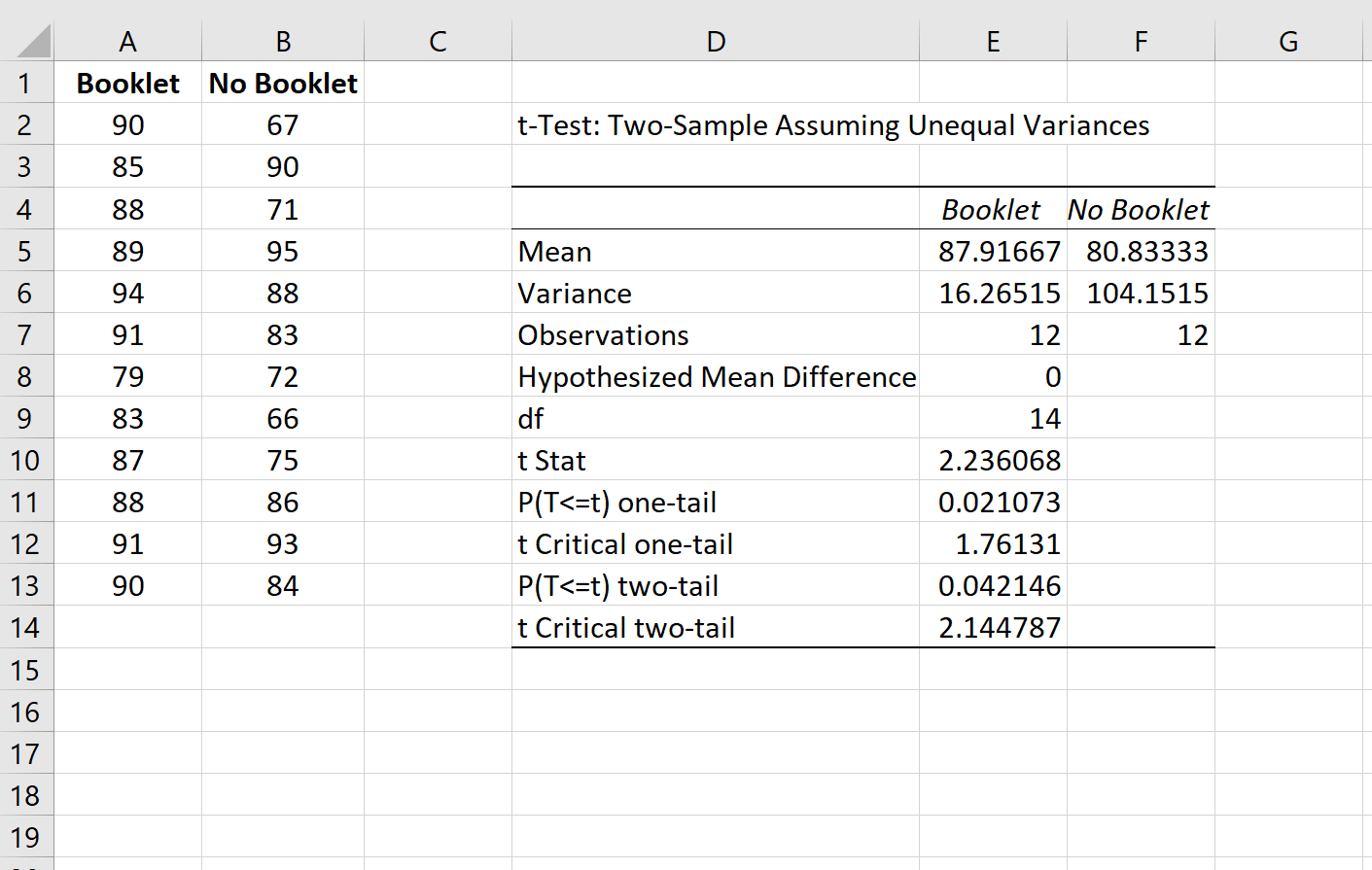
Oto jak zinterpretować wynik:

• Średnia: średni wynik egzaminu dla każdej grupy.
• Wariancja: wariancja wyników egzaminu dla każdej grupy.
• Obserwacje: wielkość próby dla każdej grupy.
• Hipotetyczna średnia różnica: średnia różnica, którą należy zastosować w hipotezie zerowej testu.
• df: Stopnie swobody stosowania statystyki testowej, obliczane jako n ₁ + n ₂ – 2.
• t Stat: Statystyka testowa dla testu.
• Jednostronny P(T<=t): Wartość p powiązana ze statystyką testową dla testu jednostronnego. Zignoruj to, ponieważ przeprowadzamy test dwustronny.
• P(T<=t) dwustronny: wartość p powiązana ze statystyką testową dla testu dwustronnego. Ponieważ jest to mniej niż 0,05, odrzucilibyśmy hipotezę zerową i doszliśmy do wniosku, że średni wynik egzaminu pomiędzy obiema grupami różni się istotnie statystycznie na poziomie α = 0,05.

Krok 3: Ogłoś wyniki.

Na koniec chcielibyśmy przedstawić wyniki naszego testu t Welcha. Oto przykład, jak to zrobić:

Przeprowadzono test t Welcha, aby ustalić, czy istnieje statystycznie istotna różnica w wynikach egzaminów pomiędzy grupą studentów, którzy korzystali z broszury przygotowującej do egzaminu w celu przygotowania się do egzaminu, a grupą, która z niej nie korzystała. Wielkość próby w obu grupach wynosiła 12 uczniów.

Test t Welcha wykazał, że istniała statystycznie istotna różnica w średnich wynikach egzaminu (t=2,236, p=0,0421) pomiędzy obiema grupami.