Wielkość efektu: co to jest i dlaczego jest taka ważna
„Istotność statystyczna jest najmniej interesującą rzeczą w wynikach. Wyniki należy opisać w kategoriach miar wielkości – nie tylko czy leczenie wpływa na ludzi, ale także w jakim stopniu na nich wpływa. -Gene V. Glass
W statystykach często używamy wartości p, aby określić, czy istnieje statystycznie istotna różnica między dwiema grupami.
Załóżmy na przykład, że chcemy wiedzieć, czy dwie różne techniki badania prowadzą do różnych wyników testów. Mamy więc grupę 20 uczniów, którzy używają jednej techniki uczenia się, aby przygotować się do testu, podczas gdy inna grupa 20 uczniów stosuje inną technikę uczenia się. Następnie dajemy każdemu uczniowi ten sam test.
Po przeprowadzeniu testu t dla dwóch próbek w celu określenia różnicy średnich stwierdzamy, że wartość p dla testu wynosi 0,001. Jeśli przyjmiemy poziom istotności 0,05, oznacza to, że istnieje statystycznie istotna różnica pomiędzy średnimi wynikami obu grup. Zatem technika badania ma wpływ na wyniki testu.
Jednakże, choć wartość p mówi nam, że technika uczenia się ma wpływ na wyniki testów, nie mówi nam o wielkości tego wpływu. Aby to zrozumieć, musimy znać wielkość efektu .
Co to jest wielkość efektu?
Wielkość efektu to sposób na ilościowe określenie różnicy między dwiema grupami.
Podczas gdy wartość p może nam powiedzieć, czy istnieje statystycznie istotna różnica między dwiema grupami, wielkość efektu może nam powiedzieć, jak duża jest ta różnica w rzeczywistości. W praktyce rozmiary efektów są znacznie bardziej interesujące i przydatne niż wartości p.
Istnieją trzy sposoby pomiaru wielkości efektu, w zależności od rodzaju przeprowadzanej analizy:
1. Standaryzowana średnia różnica
Jeśli chcesz zbadać średnią różnicę między dwiema grupami, właściwym sposobem obliczenia wielkości efektu jest użycie standaryzowanej średniej różnicy . Najpopularniejszym wzorem jest d Cohena, które oblicza się w następujący sposób:
Cohena D = ( x1 – x2 )/ s
gdzie x 1 i x 2 to średnie z próby, odpowiednio, grupy 1 i grupy 2, a s to odchylenie standardowe populacji, z której wylosowano obie grupy.
Korzystając z tego wzoru, wielkość efektu jest łatwa do zinterpretowania:
- Wartość d równa 1 wskazuje, że średnie z obu grup różnią się o jedno odchylenie standardowe.
- Wartość d równa 2 oznacza, że średnie grupowe różnią się o dwa odchylenia standardowe.
- Wartość d wynosząca 2,5 wskazuje, że te dwie średnie różnią się o 2,5 odchylenia standardowego i tak dalej.
Inny sposób interpretacji wielkości efektu jest następujący: wielkość efektu wynosząca 0,3 oznacza, że wynik przeciętnej osoby w grupie 2 jest o 0,3 odchylenia standardowego wyższy od średniej osoby w grupie 1 , a zatem przekracza wyniki wynoszące 62% wyników grupy 1 . .
Poniższa tabela przedstawia różne rozmiary efektów i odpowiadające im percentyle:
| Rozmiar efektu | Procent grupy 2 , który byłby poniżej średniej osób z grupy 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1,0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Im większa wielkość efektu, tym większa różnica między przeciętnym osobnikiem w każdej grupie.
Ogólnie rzecz biorąc, d wynoszące 0,2 lub mniej uważa się za małą wielkość efektu, d wynoszące około 0,5 uważa się za średnią wielkość efektu, a d wynoszące 0,8 lub więcej uważa się za dużą wielkość efektu.
Jeśli zatem średnie obu grup nie różnią się co najmniej o 0,2 odchylenia standardowego, różnica jest nieistotna, nawet jeśli wartość p jest istotna statystycznie.
2. Współczynnik korelacji
Jeśli chcesz zbadać związek ilościowy między dwiema zmiennymi, najczęstszym sposobem obliczenia wielkości efektu jest użycie współczynnika korelacji Pearsona . Jest to miara liniowego powiązania pomiędzy dwiema zmiennymi X i Y. Przyjmuje wartość od -1 do 1, gdzie:
- -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
- Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
- 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi
Wzór na obliczenie współczynnika korelacji Pearsona jest dość skomplikowany, ale dla zainteresowanych można go znaleźć tutaj .
Im współczynnik korelacji jest bardziej od zera, tym silniejsza jest liniowa zależność między dwiema zmiennymi. Można to również zobaczyć tworząc prosty wykres rozrzutu wartości zmiennych X i Y.
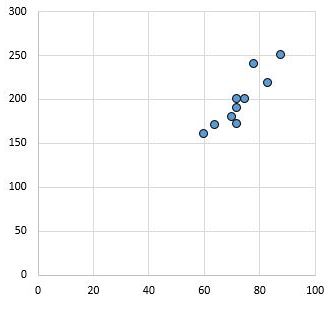
Przykładowo poniższy wykres rozrzutu przedstawia wartości dwóch zmiennych o współczynniku korelacji r = 0,94.
Wartość ta jest daleka od zera, co wskazuje, że istnieje silna dodatnia zależność pomiędzy obiema zmiennymi.
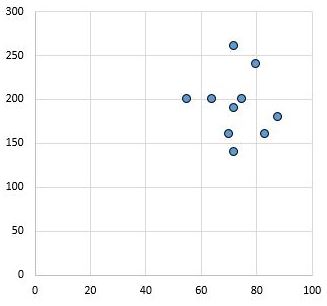
I odwrotnie, poniższy wykres rozrzutu pokazuje wartości dwóch zmiennych, które mają współczynnik korelacji r = 0,03. Wartość ta jest bliska zeru, co wskazuje, że pomiędzy obiema zmiennymi praktycznie nie ma związku.
Ogólnie rzecz biorąc, wielkość efektu uważa się za małą, jeśli wartość współczynnika korelacji Pearsona r wynosi około 0,1, średnią, jeśli r wynosi około 0,3 i dużą, jeśli r jest równe lub większe od 0,5.
3. Iloraz szans
Jeśli chcesz zbadać szanse powodzenia w grupie terapeutycznej w porównaniu z szansami powodzenia w grupie kontrolnej, najczęstszym sposobem obliczenia wielkości efektu jest użycie ilorazu szans .
Załóżmy na przykład, że mamy następującą tabelę:
| Rozmiar efektu | #Powodzenie | #Szachy |
|---|---|---|
| Grupa eksperymentalna | MA | B |
| Grupa kontrolna | VS | D |
Iloraz szans zostanie obliczony w następujący sposób:
Iloraz szans = (AD) / (BC)
Im iloraz szans jest bardziej od 1, tym większe prawdopodobieństwo, że leczenie przyniesie rzeczywisty efekt.
Korzyści ze stosowania rozmiarów efektów w porównaniu z wartościami P
Wielkości efektów mają kilka zalet w porównaniu z wartościami p:
1. Wielkość efektu pomaga nam lepiej zrozumieć, jak duża jest różnica między dwiema grupami lub jak silny jest związek między dwiema grupami. Wartość p może nam jedynie powiedzieć, czy istnieje istotna różnica lub istotne powiązanie.
2. W przeciwieństwie do wartości p, wielkości efektu można wykorzystać do ilościowego porównania wyników różnych badań przeprowadzonych w różnych warunkach. Z tego powodu w metaanalizach często wykorzystuje się rozmiary efektów.
3. Na wartości P mogą mieć wpływ duże rozmiary próbek. Im większa wielkość próby, tym większa moc statystyczna testu hipotezy, umożliwiająca wykrycie nawet małych efektów. Może to prowadzić do niskich wartości p, pomimo niewielkich rozmiarów efektu, które mogą nie mieć praktycznego znaczenia.
Prosty przykład może to jasno zilustrować: załóżmy, że chcemy wiedzieć, czy dwie techniki badania prowadzą do różnych wyników testów. Mamy grupę 20 uczniów stosujących jedną technikę nauki, a drugą grupę 20 uczniów stosującą inną technikę nauki. Następnie dajemy każdemu uczniowi ten sam test.
Średni wynik grupy 1 to 90,65 , a średni wynik grupy 2 to 90,75 . Odchylenie standardowe dla próbki 1 wynosi 2,77 , a odchylenie standardowe dla próbki 2 wynosi 2,78 .
Kiedy przeprowadzamy niezależny test t dla dwóch prób, okazuje się, że statystyka testowa wynosi -0,113 , a odpowiadająca jej wartość p wynosi 0,91 . Różnica pomiędzy średnimi wynikami testów nie jest istotna statystycznie.
Należy jednak rozważyć, czy liczebność obu próbek wynosiła 200 , ale średnie i odchylenia standardowe pozostały dokładnie takie same.
W tym przypadku niezależny test t dla dwóch próbek ujawniłby, że statystyka testowa wynosi -1,97 , a odpowiadająca jej wartość p wynosi nieco poniżej 0,05 . Różnica pomiędzy średnimi wynikami testów jest istotna statystycznie.
Podstawowym powodem, dla którego duże rozmiary próbek mogą prowadzić do statystycznie istotnych wniosków, jest wzór zastosowany do obliczenia statystyk testu t :
statystyka testowa t = [ ( x 1 – x 2 ) – re ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Należy zauważyć, że gdy n 1 i n 2 są małe, całkowity mianownik statystyki testu t jest mały. A jeśli podzielisz przez małą liczbę, otrzymasz dużą liczbę. Oznacza to, że statystyka testu t będzie duża, a odpowiadająca jej wartość p będzie mała, co doprowadzi do statystycznie istotnych wyników.
Co jest uważane za dobry rozmiar efektu?
Studenci często zadają pytanie: Jaka wielkość efektu jest uważana za dobrą?
Krótka odpowiedź: wielkość efektu nie może być „dobra” ani „zła”, ponieważ mierzy po prostu wielkość różnicy między dwiema grupami lub siłę powiązania między dwiema grupami.
Możemy jednak zastosować się do następujących praktycznych zasad, aby określić ilościowo, czy wielkość efektu jest mała, średnia czy duża:
Cohena D:
- Wartość d wynosząca 0,2 lub mniej uważa się za małą wielkość efektu.
- Wartość d wynosząca 0,5 uważa się za średnią wielkość efektu.
- Wartość d wynosząca 0,8 lub większa jest uważana za dużą wielkość efektu.
Współczynnik korelacji Pearsona
- Wartość bezwzględną r w okolicach 0,1 uważa się za małą wielkość efektu.
- Wartość bezwzględną r około 0,3 uważa się za średnią wielkość efektu.
- Wartość bezwzględna r większa niż 0,5 jest uważana za dużą wielkość efektu.
Jednakże definicja „silnej” korelacji może się różnić w zależności od dziedziny. Zapoznaj się z tym artykułem , aby lepiej zrozumieć, co jest uważane za silną korelację między różnymi branżami.