Jak wykonać wielokrotną regresję liniową w sas-ie

Wielokrotna regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między dwiema lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

W tym samouczku wyjaśniono, jak przeprowadzić wielokrotną regresję liniową w SAS-ie.

Krok 1: Utwórz dane

Załóżmy, że chcemy dopasować model regresji liniowej wielokrotnej, który wykorzystuje liczbę godzin spędzonych na nauce i liczbę zdanych egzaminów praktycznych, aby przewidzieć końcową ocenę uczniów z egzaminu:

Wynik egzaminu = β ₀ + β ₁ (godziny) + β ₂ (egzaminy przygotowawcze)

Najpierw użyjemy następującego kodu, aby utworzyć zbiór danych zawierający te informacje dla 20 uczniów:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Krok 2: Wykonaj wielokrotną regresję liniową

Następnie użyjemy proc reg , aby dopasować model regresji liniowej do danych:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

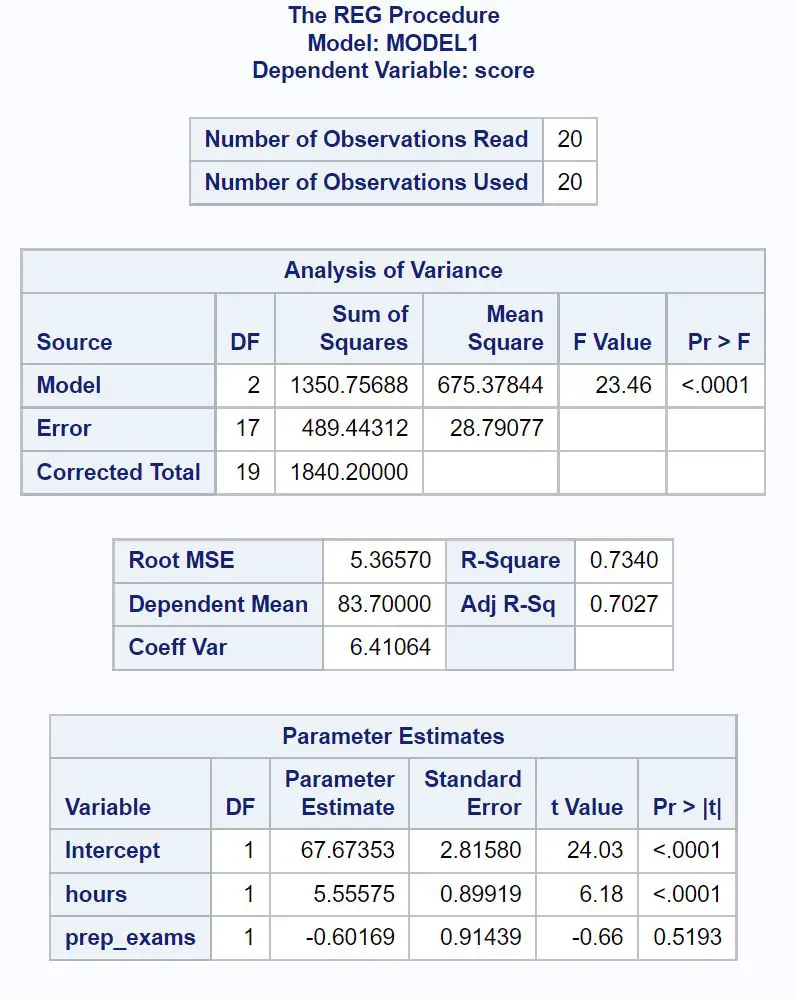
Oto jak interpretować najbardziej odpowiednie liczby w każdej tabeli:

Tabela analizy luk:

Ogólna wartość F modelu regresji wynosi 23,46 , a odpowiadająca jej wartość p wynosi <0,0001 .

Ponieważ ta wartość p jest mniejsza niż 0,05, dochodzimy do wniosku, że model regresji jako całość jest istotny statystycznie.

Tabela dopasowania modelu:

Wartość R-Square informuje nas o procentowym zróżnicowaniu wyników egzaminu, które można wytłumaczyć liczbą godzin nauki i liczbą zdanych egzaminów przygotowawczych.

Ogólnie rzecz biorąc, im większa wartość R-kwadrat modelu regresji, tym lepiej zmienne predykcyjne przewidują wartość zmiennej odpowiedzi.

W tym przypadku 73,4% różnic w wynikach egzaminów można wytłumaczyć liczbą przepracowanych godzin i liczbą zdanych egzaminów przygotowawczych.

Wartość Root MSE jest również przydatna. Stanowi to średnią odległość między obserwowanymi wartościami a linią regresji.

W tym modelu regresji zaobserwowane wartości odbiegają średnio o 5,3657 jednostki od linii regresji.

Tabela szacunków parametrów:

Możemy użyć wartości szacunkowych parametrów w tej tabeli, aby zapisać dopasowane równanie regresji:

Wynik egzaminu = 67,674 + 5,556*(godziny) – 0,602*(prep_exams)

Możemy użyć tego równania, aby znaleźć szacowany wynik egzaminu studenta na podstawie liczby godzin nauki i liczby egzaminów praktycznych, które zdawał.

Przykładowo student studiujący 3 godziny i przystępujący do 2 egzaminów przygotowawczych powinien uzyskać ocenę 83,1 :

Szacowany wynik egzaminu = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Wartość p dla godzin (<0,0001) jest mniejsza niż 0,05, co oznacza, że ma statystycznie istotny związek z wynikiem badania.

Natomiast wartość p dla egzaminów przygotowawczych (0,5193) jest nie mniejsza niż 0,05, co oznacza, że nie ma ona istotnego statystycznie związku z wynikiem egzaminu.

Możemy zdecydować się na usunięcie badań przygotowawczych z modelu, ponieważ nie są one statystycznie istotne, i zamiast tego przeprowadzić prostą regresję liniową , wykorzystując badane godziny jako jedyną zmienną predykcyjną.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak obliczyć korelację w SAS-ie
Jak wykonać prostą regresję liniową w SAS-ie
Jak wykonać jednokierunkową ANOVA w SAS