R wielokrotność lub r kwadrat: jaka jest różnica?

Kiedy dopasujesz model regresji przy użyciu większości programów statystycznych, często w wyniku zauważysz następujące dwie wartości:

Wielokrotne R: współczynnik korelacji wielokrotnej pomiędzy trzema lub większą liczbą zmiennych.

R-kwadrat: Wartość tę oblicza się jako (wielokrotne R) ² i reprezentuje część wariancjizmiennej odpowiedzi modelu regresji, którą można wyjaśnić za pomocą zmiennych predykcyjnych. Wartość ta waha się od 0 do 1.

W praktyce często interesuje nas wartość R-kwadrat, ponieważ mówi nam ona, jak przydatne są zmienne predykcyjne w przewidywaniu wartości zmiennej odpowiedzi.

Jednakże za każdym razem, gdy dodamy do modelu nową zmienną predykcyjną, R-kwadrat z pewnością wzrośnie, nawet jeśli zmienna predykcyjna nie będzie użyteczna.

Skorygowane R-kwadrat to zmodyfikowana wersja R-kwadrat, która dostosowuje liczbę predyktorów w modelu regresji. Oblicza się go w następujący sposób:

Skorygowany R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

Złoto:

• R ² : R ² modelu
• n : Liczba obserwacji
• k : Liczba zmiennych predykcyjnych

Ponieważ wartość R-kwadrat zawsze rośnie w miarę dodawania kolejnych predyktorów do modelu, skorygowana wartość R-kwadrat może służyć jako miara informująca o przydatności modelu, skorygowana na podstawie liczby predyktorów w modelu .

Aby lepiej zrozumieć każdy z tych terminów, rozważ następujący przykład.

Przykład: wielokrotne R, R-kwadrat i skorygowane R-kwadrat

Załóżmy, że mamy następujący zbiór danych zawierający trzy zmienne dla 12 różnych uczniów:

Załóżmy, że dopasowujemy model regresji liniowej, wykorzystując godziny nauki i aktualną ocenę jako zmienne predykcyjne, a wynik egzaminu jako zmienną odpowiedzi, i otrzymujemy następujący wynik:

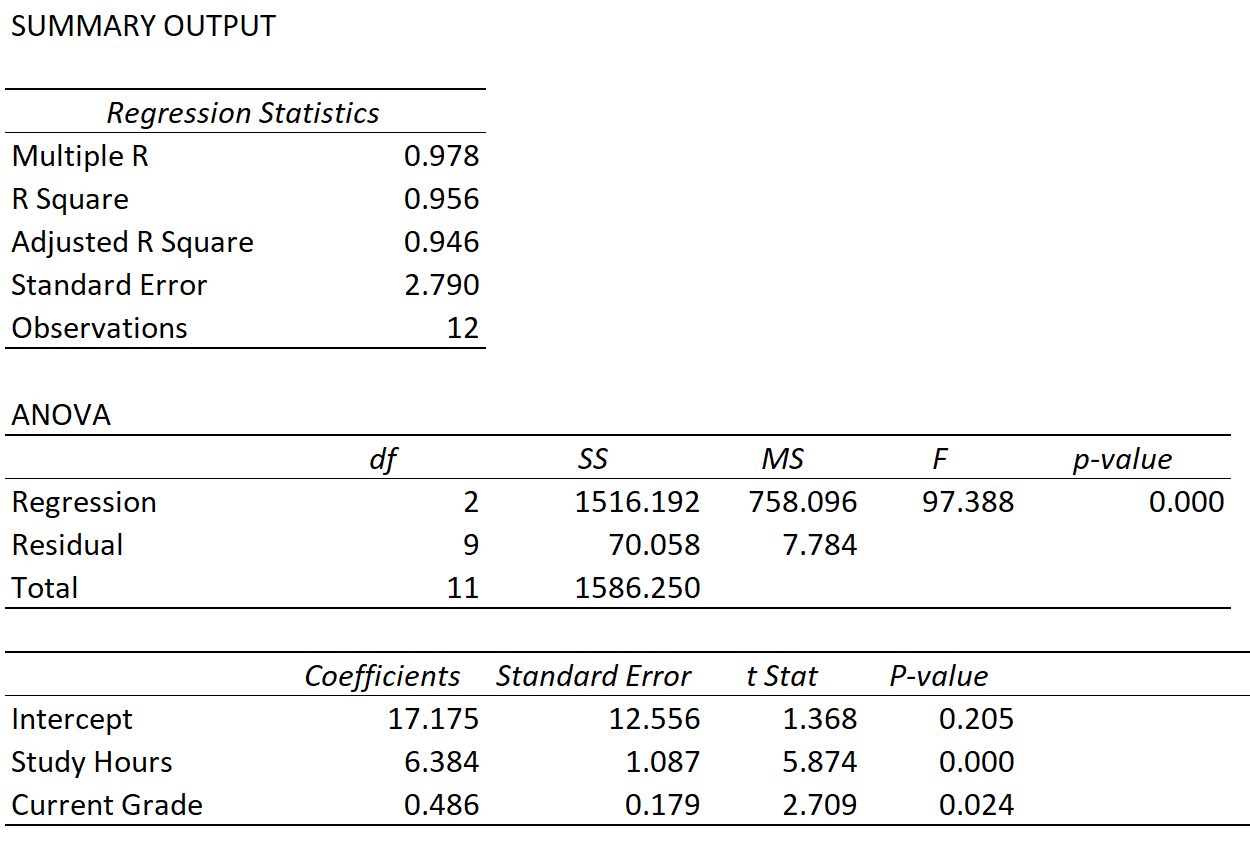
Możemy zaobserwować wartości następujących trzech wskaźników:

Wielokrotne R: 0,978 . Reprezentuje to wielokrotną korelację między zmienną odpowiedzi a dwiema zmiennymi predykcyjnymi.

R Kwadrat: 0,956 . Oblicza się to jako (wielokrotne R) ² = (0,978) ² = 0,956. Z tego wynika, że 95,6% różnic w wynikach egzaminów można wyjaśnić liczbą godzin spędzonych przez studentów na nauce oraz ich obecną oceną z kursu.

Skorygowany R-kwadrat: 0,946 . Oblicza się to w następujący sposób:

Skorygowany R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.

Stanowi to wartość R-kwadrat, skorygowaną o liczbę zmiennych predykcyjnych w modelu .

Miara ta byłaby przydatna, jeśli na przykład dopasujemy inny model regresji z 10 predyktorami i stwierdzimy, że skorygowany R-kwadrat tego modelu wynosi 0,88 . Oznaczałoby to, że model regresji zawierający tylko dwa predyktory jest lepszy, ponieważ ma wyższą skorygowaną wartość R-kwadrat.

Dodatkowe zasoby

Wprowadzenie do wielokrotnej regresji liniowej
Jaka jest dobra wartość R-kwadrat?