Współczynnik phi: definicja i przykłady

Współczynnik Phi (czasami nazywany średniokwadratowym współczynnikiem kontyngencji ) jest miarą powiązania między dwiema zmiennymi binarnymi.

Dla tabeli 2×2 danej dla dwóch zmiennych losowych x i y :

Współczynnik Phi można obliczyć w następujący sposób:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Przykład: Obliczenie współczynnika Phi

Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 25 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:

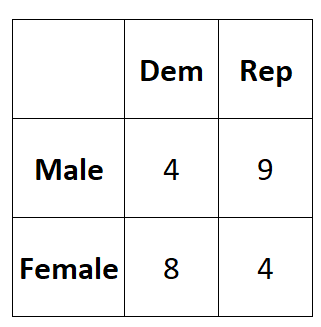
Możemy obliczyć współczynnik Phi między dwiema zmiennymi w następujący sposób:

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0,3589

Uwaga: Mogliśmy to również obliczyć za pomocą kalkulatora współczynnika Phi.

Jak interpretować współczynnik Phi

Podobnie jak współczynnik korelacji Pearsona, współczynnik Phi przyjmuje wartości od -1 do 1, gdzie:

• -1 wskazuje całkowicie ujemną zależność między dwiema zmiennymi.
• Wartość 0 oznacza brak związku między dwiema zmiennymi.
• 1 wskazuje na całkowicie pozytywną zależność pomiędzy obiema zmiennymi.

Ogólnie rzecz biorąc, im współczynnik Phi jest dalej od zera, tym silniejszy jest związek między tymi dwiema zmiennymi.

Innymi słowy, im współczynnik Phi jest dalej od zera, tym więcej jest dowodów na istnienie pewnego rodzaju systematycznego wzorca pomiędzy obiema zmiennymi.

Dodatkowe zasoby

Przewodnik po współczynniku korelacji Pearsona
Przewodnik po dokładnym teście Fishera
Przewodnik po teście niezależności chi-kwadrat