Współczynnik korelacji pearsona

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest współczynnik korelacji Pearsona (lub współczynnik korelacji liniowej) i do czego się go używa. Dzięki ćwiczeniu krok po kroku dowiesz się, jak obliczyć współczynnik korelacji Pearsona. Dodatkowo możesz znaleźć wartość współczynnika korelacji Pearsona dla dowolnego zbioru danych za pomocą kalkulatora online na końcu.

Jaki jest współczynnik korelacji Pearsona?

Współczynnik korelacji Pearsona , zwany także współczynnikiem korelacji liniowej lub po prostu współczynnikiem korelacji , jest miarą statystyczną wskazującą związek między dwiema zmiennymi.

Aby obliczyć współczynnik korelacji Pearsona pomiędzy dwiema zmiennymi, należy podzielić kowariancję tych zmiennych przez pierwiastek kwadratowy z iloczynu ich wariancji.

Zatem współczynnik korelacji Pearsona stanowi próbę ilościowego określenia liniowej zależności między dwiema ilościowymi zmiennymi losowymi. A priori numeryczna ocena korelacji między zmiennymi jest skomplikowana, ponieważ trudno jest ustalić, czy para zmiennych jest bardziej skorelowana pomiędzy if, jak w pues, celem współczynnika korelacji Pearsona jest wycena relacji między zmiennymi, aby móc porównać między nimi.

Wartość wskaźnika korelacji Pearsona mieści się w przedziale od -1 do +1 włącznie. Poniżej zobaczymy jak interpretowana jest wartość współczynnika korelacji Pearsona.

Wzór na współczynnik korelacji Pearsona

Współczynnik korelacji Pearsona dwóch zmiennych statystycznych jest równy ilorazowi kowariancji zmiennych i pierwiastka kwadratowego iloczynu wariancji każdej zmiennej.

Dlatego wzór na obliczenie współczynnika korelacji Pearsona jest następujący:

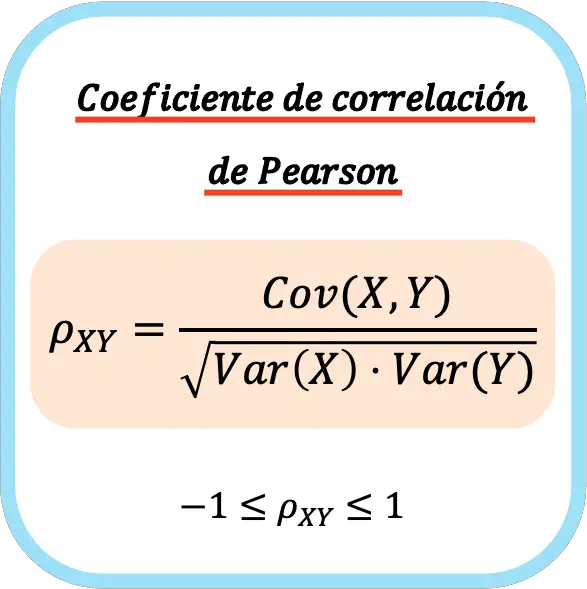
Współczynnik korelacji Pearsona, współczynnik korelacji liniowej

👉 Za pomocą poniższego kalkulatora możesz obliczyć współczynnik korelacji Pearsona dla dowolnego zbioru danych.

Gdy współczynnik korelacji Pearsona oblicza się dla populacji, zwykle wyraża się go grecką literą ρ. Ale gdy współczynnik jest obliczany w odniesieniu do próbki, litera r jest zwykle używana jako symbol.

Należy pamiętać, że aby określić współczynnik korelacji Pearsona, niezbędna jest umiejętność obliczenia kowariancji między dwiema zmiennymi i wariancji zmiennej. Ponadto musisz zrozumieć, co oznaczają te miary statystyczne. Dlatego przed kontynuowaniem wyjaśnień zaleca się przeczytanie następujących dwóch artykułów:

➤ Zobacz: jak obliczyć kowariancję
➤ Zobacz: jak obliczyć lukę

Przykład obliczenia współczynnika korelacji Pearsona

Biorąc pod uwagę definicję współczynnika korelacji Pearsona i jego wzór, poniżej znajduje się przykład krok po kroku, dzięki któremu można zobaczyć, jak jest on obliczany.

Oblicz współczynnik korelacji Pearsona pomiędzy następującymi dwiema zmiennymi ciągłymi:

Przed obliczeniem współczynnika korelacji Pearsona przedstawimy zbiór danych na wykresie rozrzutu, aby przeanalizować związek między dwiema zmiennymi:

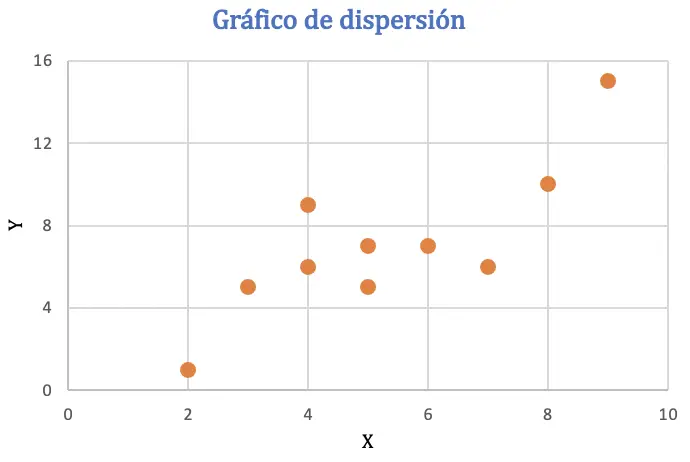
Z wykresu punktowego można wywnioskować, że dane mogą wykazywać tendencję dodatnią, czyli innymi słowy, gdy wartość jednej zmiennej wzrasta, druga zmienna również wzrasta. Aby sprawdzić korelację, znajdziemy współczynnik Pearsona.

Pierwszą rzeczą do zrobienia jest znalezienie średniej arytmetycznej każdej zmiennej z osobna, która jest równa całkowitej sumie danych podzielonej przez liczbę obserwacji.

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

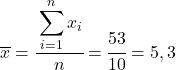
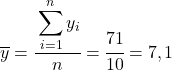
Teraz, gdy znamy średnią każdej zmiennej, musimy dodać następujące kolumny do tabeli danych:

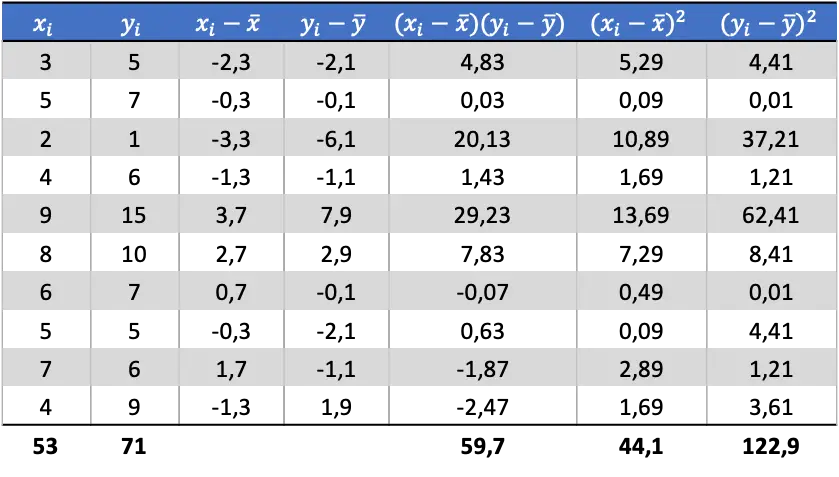
Tabela danych do obliczeń współczynnika Pearsona

Z obliczonych danych w tabeli określamy wartości kowariancji i wariancji (jeśli nie pamiętasz, jak to zrobiono, powyżej znajdują się dwa linki, w których jest to szczegółowo wyjaśnione):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

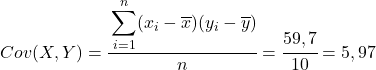
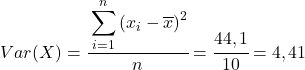
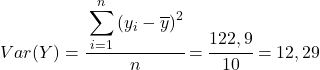
Na koniec wystarczy zastosować wzór na współczynnik korelacji Pearsona, aby uzyskać jego wartość:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

Współczynnik korelacji Pearsona ma wartość bardzo bliską 1, co oznacza, że te dwie zmienne mają dość silną dodatnią korelację.

Jak widać, do określenia współczynnika korelacji Pearsona bardzo przydatne jest użycie programów takich jak Excel, aby szybciej wykonać obliczenia kolumnowe.

Kalkulator współczynnika korelacji Pearsona

Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć współczynnik korelacji Pearsona między dwiema zmiennymi. Należy rozdzielić pary danych tak, aby w pierwszym polu znajdowały się tylko wartości jednej zmiennej, a w drugim tylko wartości drugiej zmiennej.

Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Interpretacja współczynnika korelacji Pearsona

W tej sekcji zobaczymy, jak interpretować współczynnik korelacji Pearsona, ponieważ nie wystarczy znać jego wartość, ale trzeba wiedzieć, jak analizować jego znaczenie.

Zatem interpretacja współczynnika korelacji Pearsona zależy od jego wartości:

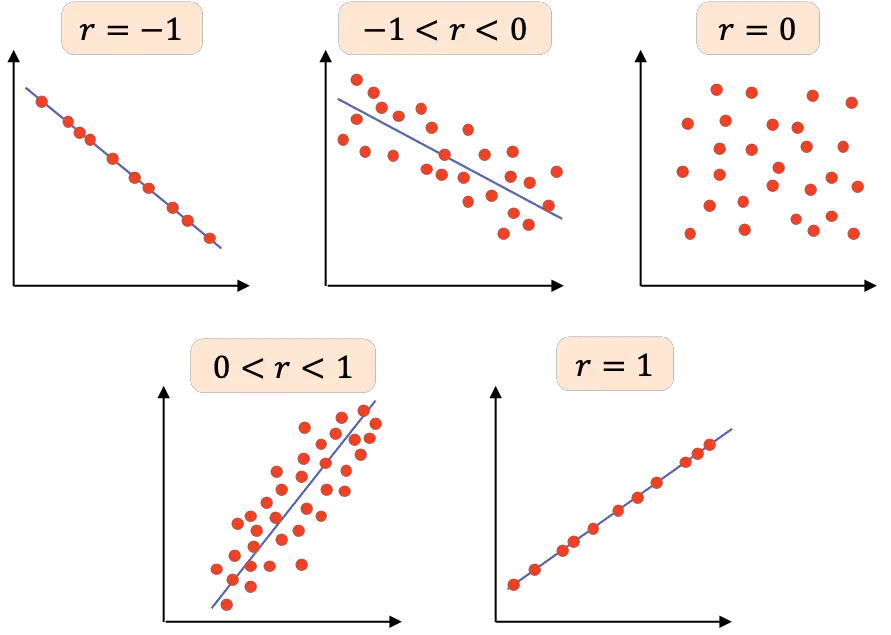
r=-1 : obie zmienne mają idealną ujemną korelację, więc możemy narysować linię o nachyleniu ujemnym, w której wszystkie punkty się łączą.
-1<r<0 : korelacja między dwiema zmiennymi jest ujemna, więc gdy jedna zmienna rośnie, druga maleje. Im wartość jest bliższa -1, tym bardziej ujemnie powiązane są zmienne.
r=0 : korelacja między dwiema zmiennymi jest bardzo słaba, w rzeczywistości zależność liniowa między nimi wynosi zero. Nie oznacza to, że zmienne są niezależne, ponieważ mogą mieć zależność nieliniową.
0<r<1 : korelacja między dwiema zmiennymi jest dodatnia, im wartość jest bliższa +1, tym silniejszy jest związek między zmiennymi. W tym przypadku jedna zmienna ma tendencję do zwiększania wartości, podczas gdy druga również rośnie.
r=1 : obie zmienne mają doskonałą dodatnią korelację, to znaczy mają dodatnią zależność liniową.

Podsumowując, poniższa tabela przedstawia różne interpretacje współczynnika korelacji Pearsona:

Wartość	Interpretacja
r=-1	Idealna korelacja ujemna.
-1<r<0	Korelacja ujemna: im korelacja jest bliższa -1, tym jest silniejsza.
r=0	Zerowa korelacja liniowa.
0<r<1	Korelacja dodatnia: im korelacja jest bliższa +1, tym jest silniejsza.
r=1	Idealna pozytywna korelacja.

Należy pamiętać, że nawet jeśli istnieje związek między dwiema zmiennymi, nie oznacza to, że istnieje między nimi związek przyczynowy, czyli korelacja między dwiema zmiennymi nie oznacza, że zmiana zmiennej jest przyczyną zmiany zmiennej. inna zmienna.

Na przykład, jeśli odkryjemy, że istnieje pozytywny związek pomiędzy produkcją dwóch różnych hormonów w organizmie, nie jest konieczne, aby wzrost poziomu jednego hormonu prowadził do wzrostu poziomu drugiego. Może się zdarzyć, że organizm wytwarza oba hormony, ponieważ potrzebuje obu do walki z chorobą i dlatego zwiększa poziom obu hormonów jednocześnie, w takim przypadku przyczyną będzie choroba. Aby ustalić, czy istnieje związek przyczynowy między tymi dwoma hormonami, należy przeprowadzić dalsze badania.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej