Współczynnik korelacji wewnątrzklasowej: definicja + przykład

Do pomiaru wiarygodności wyników w badaniach, w których uczestniczy co najmniej dwóch oceniających, stosuje się współczynnik korelacji wewnątrzklasowej (ICC).

Wartość ICC może mieścić się w przedziale od 0 do 1, gdzie 0 oznacza brak wiarygodności wśród oceniających, a 1 oznacza doskonałą wiarygodność wśród oceniających.

Mówiąc najprościej, ICC służy do określenia, czy elementy (lub tematy) mogą być wiarygodnie ocenione przez różnych oceniających.

Istnieje kilka różnych wersji ICC, które można obliczyć, w zależności od następujących trzech czynników:

• Model: jednokierunkowe efekty losowe, dwukierunkowe efekty losowe lub dwukierunkowe efekty mieszane
• Rodzaj relacji: konsekwencja lub absolutna zgoda
• Jednostka: pojedynczy oceniający lub średnia oceniających

Oto krótki opis trzech różnych modeli :

1. Model jednokierunkowych efektów losowych: Model ten zakłada, że każdy przedmiot jest oceniany przez inną grupę losowo wybranych ewaluatorów. W tym modelu oceniający są uważani za źródło efektów losowych. Model ten jest rzadko stosowany w praktyce, gdyż do oceny każdego przedmiotu na ogół wykorzystywana jest ta sama grupa asesorów.

2. Model dwukierunkowych efektów losowych: Model ten zakłada, że grupa oceniających k jest wybierana losowo z populacji, a następnie wykorzystywana do oceny badanych. Stosując ten model, oceniający i badani są uważani za źródła efektów losowych. Model ten jest często stosowany, gdy chcemy uogólnić nasze wyniki na osoby oceniające podobne do tych zastosowanych w badaniu.

3. Dwukierunkowy model efektów mieszanych: Model ten zakłada również, że grupa oceniających k jest wybierana losowo z populacji, a następnie wykorzystywana do oceny badanych. Model ten zakłada jednak, że wybrana przez nas grupa oceniających to jedyne osoby oceniające, które nas interesują, co oznacza, że nie chcemy uogólniać naszych wyników na innych oceniających, którzy również mogliby mieć podobne cechy do oceniających wykorzystanych w badaniu.

Oto krótki opis dwóch różnych typów relacji, które możemy chcieć zmierzyć:

1. Spójność: interesują nas systematyczne różnice między ocenami sędziów (np. czy sędziowie ocenili podobne tematy jako niskie i wysokie?)

2. Zgodność absolutna: interesują nas bezwzględne różnice pomiędzy ocenami sędziów (np. jaka jest bezwzględna różnica pomiędzy ocenami sędziego A i sędziego B?)

Oto krótki opis dwóch różnych jednostek , które mogą nas zainteresować:

1. Pojedynczy recenzent: Jako podstawę pomiaru chcemy wykorzystywać wyłącznie oceny jednego recenzenta.

2. Średnia ocen: Jako podstawę pomiaru chcemy wykorzystać średnią ocen wszystkich sędziów.

Uwaga: Jeśli chcesz zmierzyć poziom zgodności między dwoma oceniającymi, którzy pominęli każdy z elementów w wyniku dychotomicznym , powinieneś zamiast tego użyć Kappa Cohena .

Jak interpretować współczynnik korelacji wewnątrzklasowej

Według Koo i Li , oto jak interpretować wartość współczynnika korelacji wewnątrzklasowej:

• Mniej niż 0,50: słaba niezawodność
• Między 0,5 a 0,75: Umiarkowana niezawodność
• Między 0,75 a 0,9: Dobra niezawodność
• Większa niż 0,9: Doskonała niezawodność

Poniższy przykład pokazuje, jak w praktyce obliczyć współczynnik korelacji wewnątrzklasowej.

Przykład: Obliczenie współczynnika korelacji wewnątrzklasowej

Załóżmy, że czterech różnych sędziów zostaje poproszonych o ocenę jakości 10 różnych egzaminów wstępnych na studia. Wyniki przedstawiono poniżej:

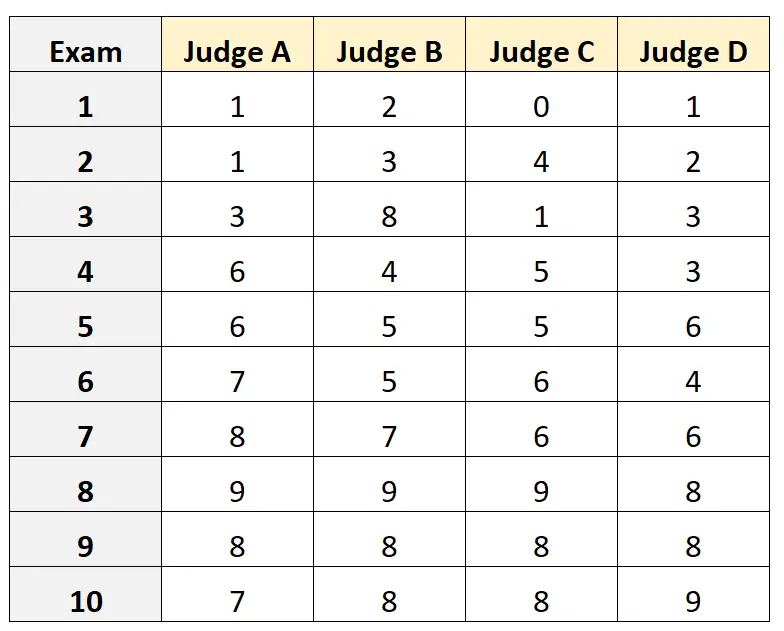
Załóżmy, że czterech sędziów zostało losowo wybranych z populacji wykwalifikowanych sędziów do egzaminu wstępnego i chcieliśmy zmierzyć absolutną zgodność między sędziami, a jako podstawę naszego pomiaru chcieliśmy wykorzystać wyniki z perspektywy tylko jednego oceniającego.

Możemy użyć następującego kodu w języku R, aby dopasować model dwukierunkowych efektów losowych , stosując absolutną zgodność jako relację między oceniającymi i używając pojedynczej jednostki jako jednostki zainteresowania:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Stwierdzono, że współczynnik korelacji wewnątrzklasowej (ICC) wynosi 0,782 .

Opierając się na praktycznych zasadach interpretacji ICC, można dojść do wniosku, że ICC wynoszący 0,782 wskazuje, że egzaminy mogą być oceniane z „dobrą” wiarygodnością przez różnych oceniających.

Dodatkowe zasoby

Poniższe samouczki zawierają szczegółowe wyjaśnienia dotyczące obliczania ICC w różnych programach statystycznych:

Jak obliczyć współczynnik korelacji wewnątrzklasowej w programie Excel
Jak obliczyć współczynnik korelacji wewnątrzklasowej w R
Jak obliczyć współczynnik korelacji wewnątrzklasowej w Pythonie