Jak obliczyć współczynnik phi w r

Współczynnik Phi (czasami nazywany średniokwadratowym współczynnikiem kontyngencji ) jest miarą powiązania między dwiema zmiennymi binarnymi.

Dla tabeli 2×2 danej dla dwóch zmiennych losowych x i y :

Współczynnik Phi można obliczyć w następujący sposób:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Przykład: Obliczenie współczynnika Phi w R

Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy więc prostą losową próbę 25 wyborców i pytamy ich o preferencje dotyczące partii politycznej.

Wyniki badania prezentuje poniższa tabela:

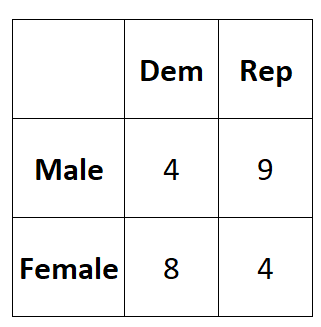
Możemy użyć następującego kodu, aby wprowadzić te dane do macierzy 2×2 w R:

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

Następnie możemy użyć funkcji phi() z pakietu psych do obliczenia współczynnika Phi pomiędzy dwiema zmiennymi:

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Współczynnik Phi okazuje się wynosić -0,36 .

Pamiętaj, że funkcja phi domyślnie zaokrągla do 2 cyfr, ale możesz określić funkcję zaokrąglającą do dowolnej liczby cyfr:

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

Jak interpretować współczynnik Phi

Podobnie jak współczynnik korelacji Pearsona, współczynnik Phi przyjmuje wartości od -1 do 1, gdzie:

• -1 wskazuje całkowicie ujemną zależność między dwiema zmiennymi.
• Wartość 0 oznacza brak związku między dwiema zmiennymi.
• 1 wskazuje na całkowicie pozytywną zależność pomiędzy obiema zmiennymi.

Ogólnie rzecz biorąc, im współczynnik Phi jest dalej od zera, tym silniejszy jest związek między tymi dwiema zmiennymi.

Innymi słowy, im współczynnik Phi jest dalej od zera, tym więcej jest dowodów na istnienie pewnego rodzaju systematycznego wzorca pomiędzy obiema zmiennymi.

Dodatkowe zasoby

Wprowadzenie do współczynnika Phi
Kalkulator współczynnika Phi