Co to jest współzmienna w statystyce?

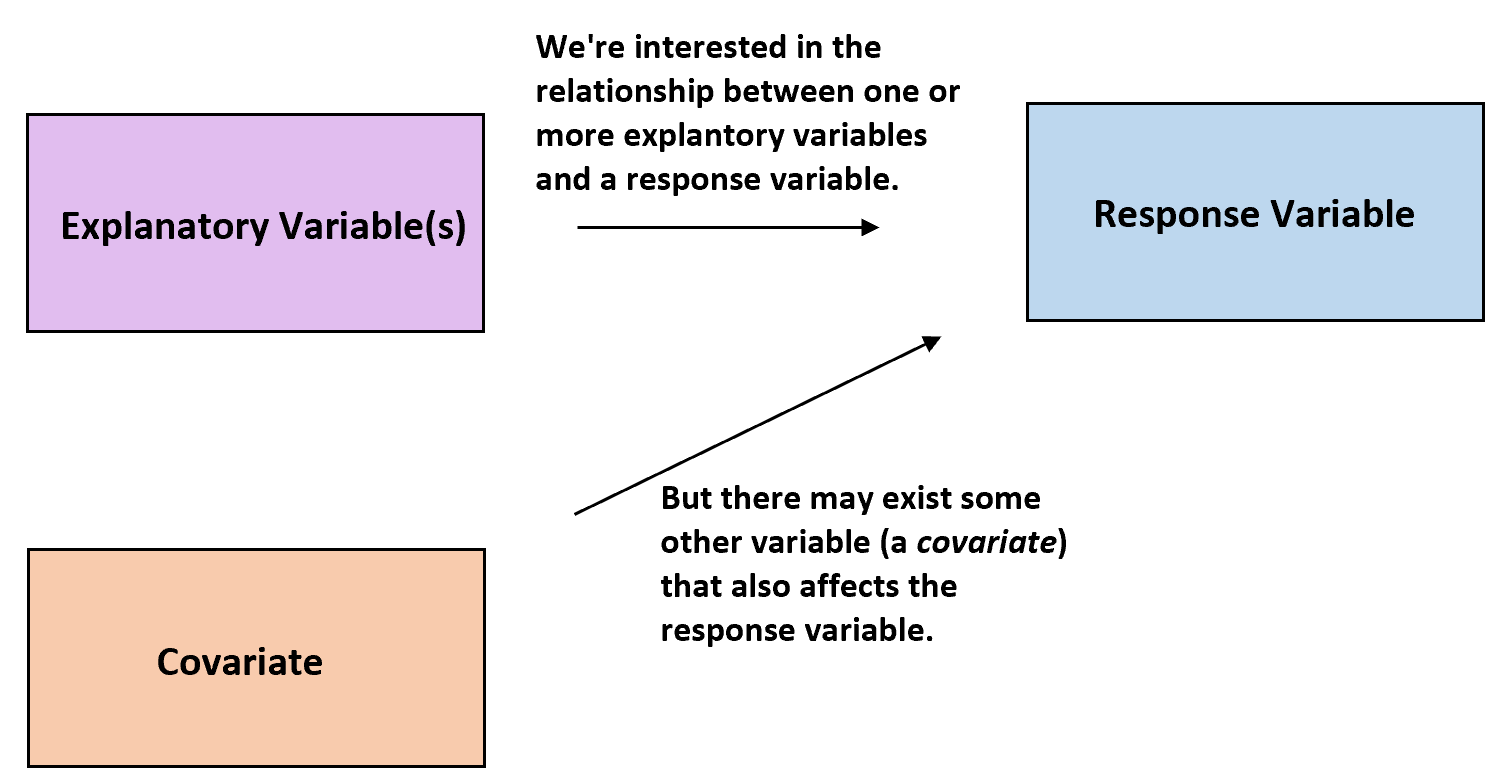
W statystyce badacze często chcą zrozumieć związek między jedną lub większą liczbą zmiennych objaśniających a zmienną odpowiedzi .

Może się jednak zdarzyć, że inne zmienne mogą wpływać na zmienną odpowiedzi i nie będą interesujące dla badaczy. Zmienne te nazywane są współzmiennymi .

Współzmienne: Zmienne, które wpływają na zmienną odpowiedzi, ale nie są przedmiotem zainteresowania w badaniu.

Załóżmy na przykład, że badacze chcą wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych średnich wyników testów w danej szkole. Technika nauki jest zmienną objaśniającą, a wynik egzaminu zmienną odpowiedzi.

Jednakże w obrębie trzech grup z pewnością będą występować różnice w możliwościach uczenia się uczniów. Jeśli nie zostanie to wzięte pod uwagę, będą to niewyjaśnione różnice w obrębie badania i utrudnią określenie prawdziwego związku pomiędzy techniką badania a wynikami badania.

Jednym ze sposobów wyjaśnienia tego może być użycie aktualnej oceny ucznia na zajęciach jako współzmiennej . Powszechnie wiadomo, że obecna ocena ucznia jest prawdopodobnie skorelowana z jego przyszłymi wynikami na egzaminie.

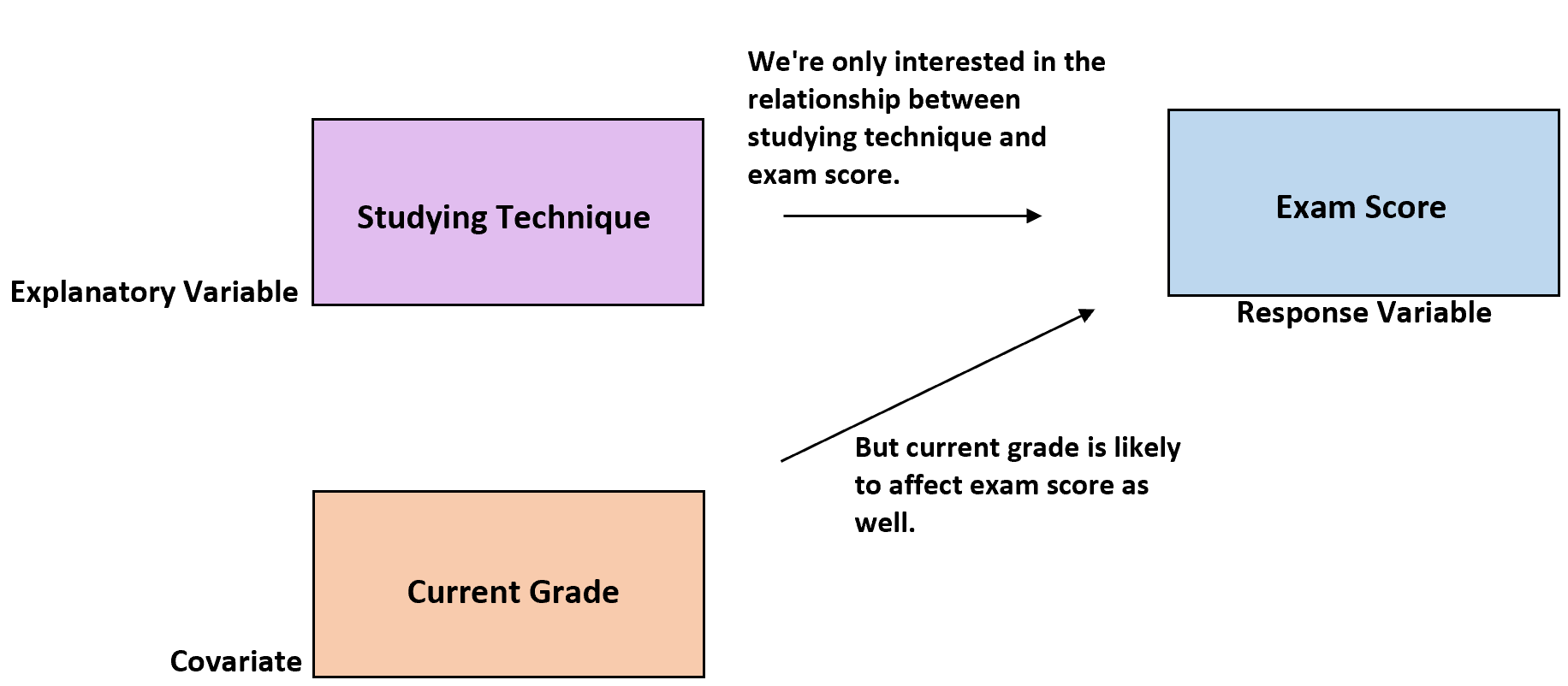
Tak więc, chociaż bieżąca ocena nie jest zmienną interesującą w tym badaniu, można ją uwzględnić jako zmienną towarzyszącą, aby badacze mogli sprawdzić, czy technika uczenia się wpływa na wyniki egzaminu, nawet po uwzględnieniu aktualnej oceny ucznia w klasie.

Współzmienne pojawiają się najczęściej w dwóch rodzajach kontekstów: ANOVA (analiza wariancji) i regresja.

Współzmienne w ANOVA

Kiedy przeprowadzamy ANOVA (niezależnie od tego, czy jest to jednokierunkowa ANOVA , dwukierunkowa ANOVA , czy coś bardziej złożonego), chcemy wiedzieć, czy istnieje różnica między średnimi z trzech lub więcej niezależnych grup.

W naszym poprzednim przykładzie chcieliśmy zrozumieć, czy istnieje różnica w średnich wynikach egzaminów pomiędzy trzema różnymi technikami uczenia się. Aby to zrozumieć, mogliśmy przeprowadzić jednokierunkową ANOVA.

Ponieważ jednak wiedzieliśmy, że bieżąca ocena ucznia również może mieć wpływ na wyniki egzaminu, mogliśmy uwzględnić ją jako współzmienną i zamiast tego przeprowadzić ANCOVA (analizę kowariancji).

Jest to podobne do ANOVA, z tą różnicą, że uwzględniamy zmienną ciągłą (bieżącą ocenę ucznia) jako współzmienną , abyśmy mogli zrozumieć, czy istnieje różnica w średnich wynikach egzaminu pomiędzy trzema technikami punktacji. studiów, nawet po uwzględnieniu wyników studenta. aktualna ocena .

Współzmienne w regresji

Kiedy przeprowadzamy regresję liniową, chcemy określić ilościowo związek między jedną lub większą liczbą zmiennych objaśniających a zmienną odpowiedzi.

Na przykład moglibyśmy przeprowadzić prostą regresję liniową , aby określić ilościowo związek między powierzchnią a cenami nieruchomości w określonym mieście. Wiadomo jednak, że wiek domu to także zmienna wpływająca na cenę nieruchomości.

W szczególności starsze domy mogą być skorelowane z niższymi cenami nieruchomości. W tym przypadku wiek domu byłby współzmienną , ponieważ tak naprawdę nie jesteśmy zainteresowani jego badaniem, ale wiemy, że ma to wpływ na ceny domów.

Możemy zatem uwzględnić wiek domu jako zmienną objaśniającą i przeprowadzić wielokrotną regresję liniową, wykorzystując powierzchnię i wiek domu jako zmienne objaśniające oraz cenę domu jako zmienną odpowiedzi.

Zatem współczynnik regresji dla metra kwadratowego pokaże nam średnią zmianę ceny domu związaną ze wzrostem powierzchni o jedną jednostkę po uwzględnieniu wieku domu .

Dodatkowe zasoby

Wprowadzenie do ANCOVA (analiza wariancji)
Jak interpretować współczynniki regresji
Jak wykonać ANCOVA w programie Excel
Jak wykonać wielokrotną regresję liniową w programie Excel