Fabuła pudełkowa i wąsowa
W tym artykule wyjaśniono, czym jest wykres pudełkowy, znany również jako wykres pudełkowy. Poznasz sposób tworzenia tego typu diagramów statystycznych oraz rozwiązane ćwiczenie dotyczące diagramu pudełkowego i wąsów oraz jego interpretację.
Co to jest fabuła pudełkowa i wąsowa?
Wykres pudełkowy , zwany także wykresem pudełkowym lub wykresem pudełkowym , to wykres, który wizualnie przedstawia zbiór danych statystycznych za pomocą kwartylów.
Główną cechą wykresu pudełkowego i wąsowego jest to, że pozwala szybko wizualizować rozproszenie serii danych, ponieważ wskazuje kwartyle, medianę, wartości ekstremalne i wartości odstające danych.
Zatem tego typu diagram składa się z prostokątnego pudełka i kilku linii (lub wąsów), z których wyłaniają się następujące wartości:
- Granice pudełka wyznaczają pierwszy i trzeci kwartyl (Q 1 i Q 3 ). A pionowa linia wewnątrz pudełka to mediana (równoważna drugiemu kwartylowi Q2 ).
- Granice wąsów (lub ramion) to wartości ekstremalne , czyli minimalna i maksymalna wartość serii danych.
- Punkty poza wąsami to wartości odstające , czyli innymi słowy dane, które prawdopodobnie zostały błędnie zmierzone i dlatego nie powinny być brane pod uwagę w badaniu statystycznym.
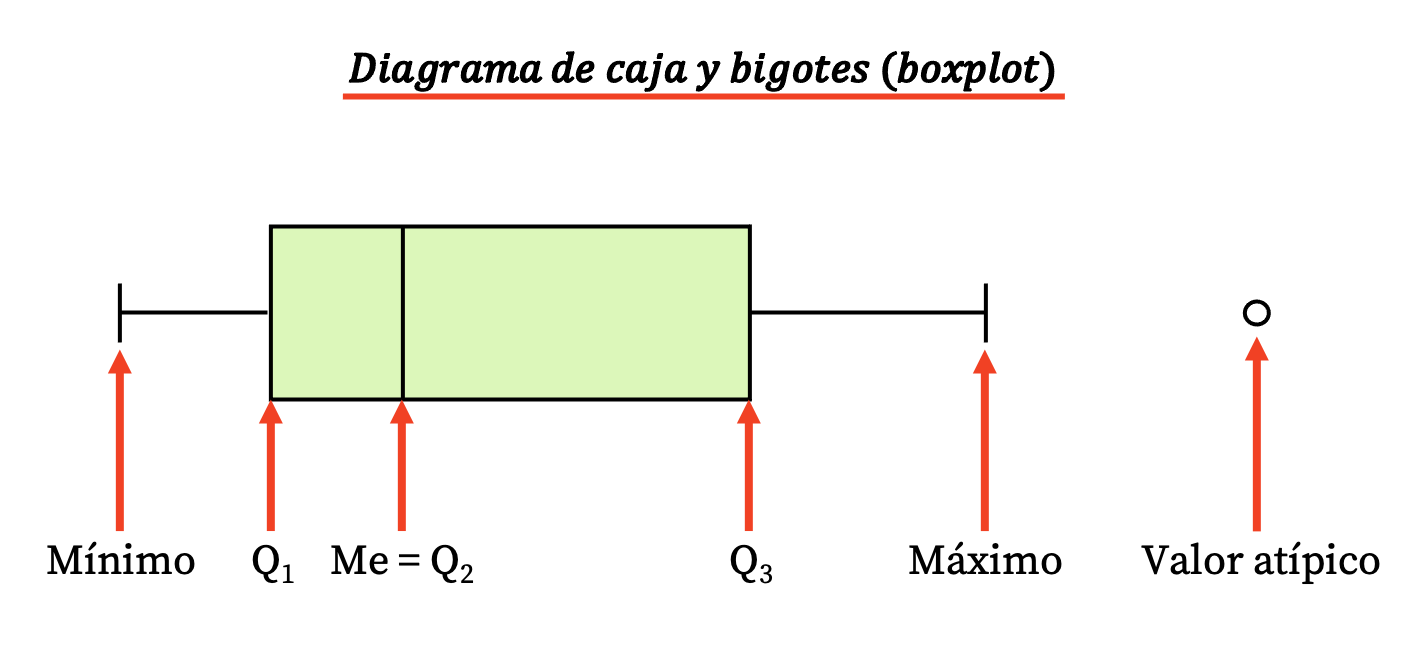
Należy zauważyć, że różnica między trzecim a pierwszym kwartylem to rozstęp międzykwartylowy (lub rozstęp międzykwartylowy), kolejna miara rozproszenia statystycznego.
Wykresy pudełkowe i wąsowe są bardzo przydatne do porównywania zmiennych numerycznych. Nie nadaje się jednak do reprezentowania zmiennych kategorycznych.
Jak utworzyć wykres pudełka i wąsów
Aby utworzyć wykres pudełkowy i wąsowy (lub wykres pudełkowy) na podstawie serii danych, należy wykonać następujące kroki:
- Uporządkuj przykłady danych statystycznych.
- Oblicz kwartyle (Q 1 , Q 2 i Q 3 ) i przedstaw je w postaci ramki na diagramie. Pierwszy i trzeci kwartyl odpowiadają granicom pudełka i aby przedstawić medianę (drugi kwartyl), należy narysować linię wewnątrz pudełka, w którym znajduje się jej wartość.
- Oblicz rozstęp międzykwartylowy równy trzeciemu kwartylowi minus pierwszy kwartyl.
- Oblicz dopuszczalne wartości LI i LS, których wzory to:
- Zidentyfikuj próbki odstające, które są wartościami mniejszymi niż LI lub większymi niż LS. Przedstaw te wartości poza zakresem wąsów za pomocą kropek.
- Zidentyfikuj i przedstaw wartości ekstremalne, które są wartością najmniejszą i największą w przedziale utworzonym przez LI i LS. Wartości te reprezentują koniec dwóch wąsów na schemacie.
![]()
![]()
![]()
Przykład wykresu pudełkowego i wąsów
Biorąc pod uwagę definicję i teorię wykresu pudełkowego (lub wykresu pudełkowego), poniżej znajdziesz konkretny przykład pozwalający lepiej zrozumieć koncepcję i zobaczyć, jak przeprowadzany jest tego typu wykres statystyczny.
- Narysuj wykres pudełkowy następującego zbioru danych statystycznych.

W tym przypadku dane są już uporządkowane od najmniejszych do największych, więc nie są konieczne żadne zmiany. W przeciwnym razie powinniśmy najpierw posortować przykładowe dane.
Po drugie, wyodrębniamy kwartyle próbki:
![]()
![]()
![]()
Po obliczeniu trzech kwartylów znajdujemy rozstęp międzykwartylowy, odejmując kwartyl 3 minus kwartyl 1:
![]()
Obliczamy teraz limity LI i LS, czyli wartości, z których dane uznaje się za nietypowe. Aby to zrobić, musisz użyć następujących formuł:
![]()
![]()
Zatem w tym przypadku mamy dwie wartości odstające, ponieważ 3,02 jest mniejsze niż 3,16, a 5,71 jest większe niż 5,56.
![]()
Na koniec pozostaje zidentyfikować wartości ekstremalne, które są minimum i maksimum wszystkich danych znajdujących się w przedziale [LI, LS]. Dlatego w naszym przykładzie minimalna wartość wynosi 3,70, a maksymalna wartość to 4,81.
![]()
![]()
Tak więc, kiedy już zidentyfikowaliśmy wszystkie wartości pudełka i wykresu wąsów, pozostaje jedynie sporządzić reprezentację graficzną:
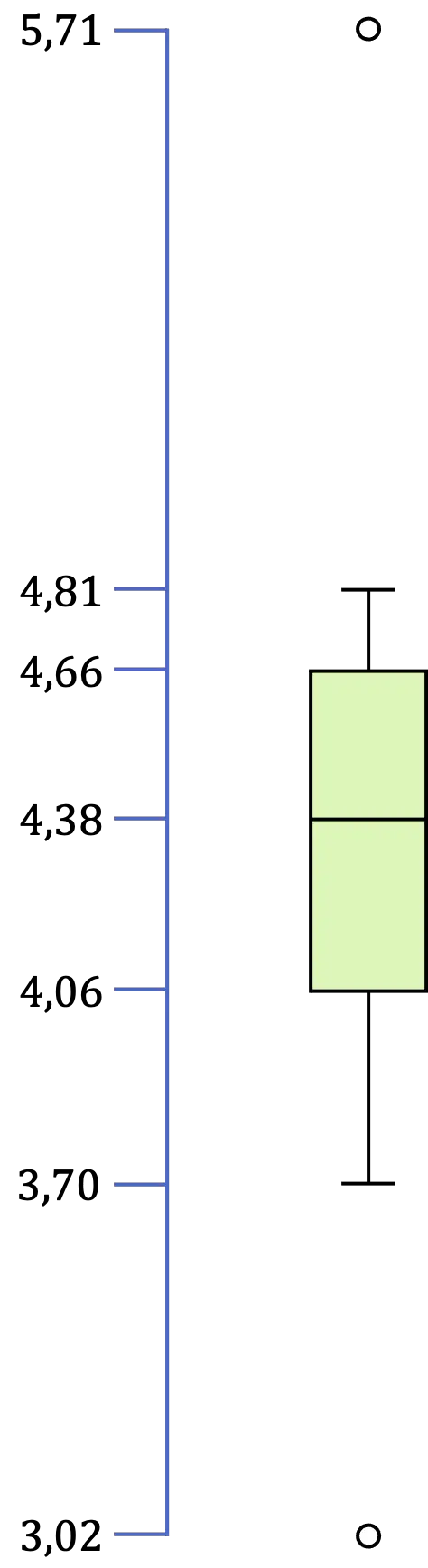
Do czego służy działka pudełkowa i wąsowa?
Na koniec zobaczmy, do czego służy i jak interpretować wykres pudełkowy i wąsowy (lub wykres pudełkowy).
Oczywiście wykres pudełkowy i wąsowy jest bardzo przydatny do szybkiego poznania kwartylów, rozstępu międzykwartylowego, mediany, wartości ekstremalnych i wartości odstających serii danych, ponieważ wszystkie te miary statystyczne można zidentyfikować za pomocą prostego widoku.
Dodatkowo do analizy symetrii próby statystycznej wykorzystuje się wykres pudełkowy i wąsowy, ponieważ wizualnie przedstawia on cały zbiór danych. Jeżeli mediana nie znajduje się pośrodku prostokąta, oznacza to, że próbka nie jest symetryczna.
Podobnie wykresy pudełkowe są szeroko stosowane na giełdzie w celu przedstawienia zmian ceny akcji w pewnym okresie czasu, ponieważ pozwalają zobaczyć wartość maksymalną, minimalną i wartości pośrednie w krótkim czasie. czasu i tym samym podejmować szybsze decyzje.