Jak wykreślić wyniki wielokrotnej regresji liniowej w r

Kiedy przeprowadzamy prostą regresję liniową w R, łatwo jest wizualizować dopasowaną linię regresji, ponieważ pracujemy tylko z jedną zmienną predykcyjną i jednązmienną odpowiedzi .

Na przykład poniższy kod pokazuje, jak dopasować prosty model regresji liniowej do zbioru danych i wykreślić wyniki:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

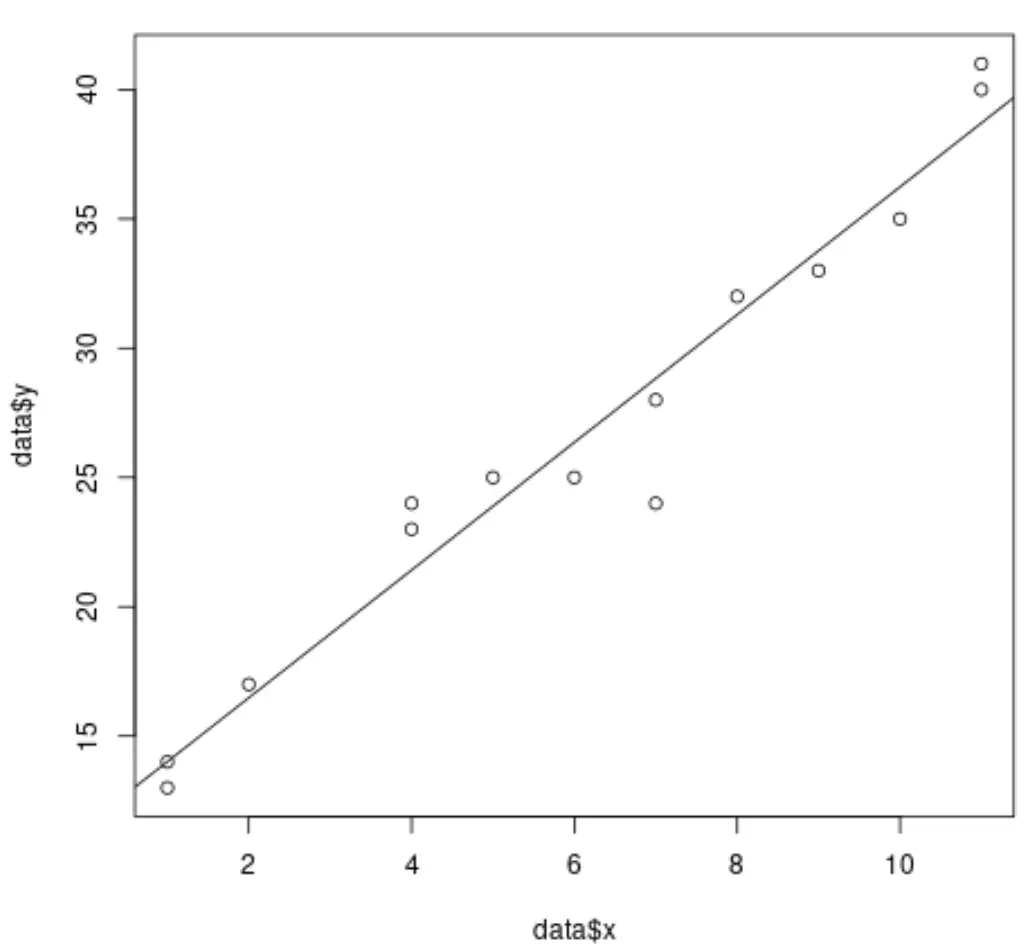
Jednakże, gdy przeprowadzamy wielokrotną regresję liniową, wizualizacja wyników staje się trudna, ponieważ istnieje wiele zmiennych predykcyjnych i nie możemy po prostu wykreślić linii regresji na wykresie 2D.

Zamiast tego możemy użyć dodanych wykresów zmiennych (czasami nazywanych „wykresami regresji częściowej”), które są indywidualnymi wykresami przedstawiającymi związek między zmienną odpowiedzi a zmienną predykcyjną, kontrolując jednocześnie obecność innych zmiennych predykcyjnych w modelu .

Poniższy przykład pokazuje, jak przeprowadzić wielokrotną regresję liniową w R i wizualizować wyniki za pomocą dołączonych wykresów zmiennych.

Przykład: wykreślanie wyników wielokrotnej regresji liniowej w R

Załóżmy, że dopasowujemy następujący model regresji liniowej do zbioru danych w R, korzystając z wbudowanego zbioru danych mtcars :

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Z wyników widać, że wartość p dla każdego ze współczynników jest mniejsza niż 0,1. Dla uproszczenia przyjmiemy, że każda ze zmiennych predykcyjnych jest istotna i powinna zostać uwzględniona w modelu.

Aby utworzyć wykresy dołączonych zmiennych, możemy użyć funkcji avPlots() z pakietu car :

 #load car package
library(car)

#produce added variable plots
avPlots(model)

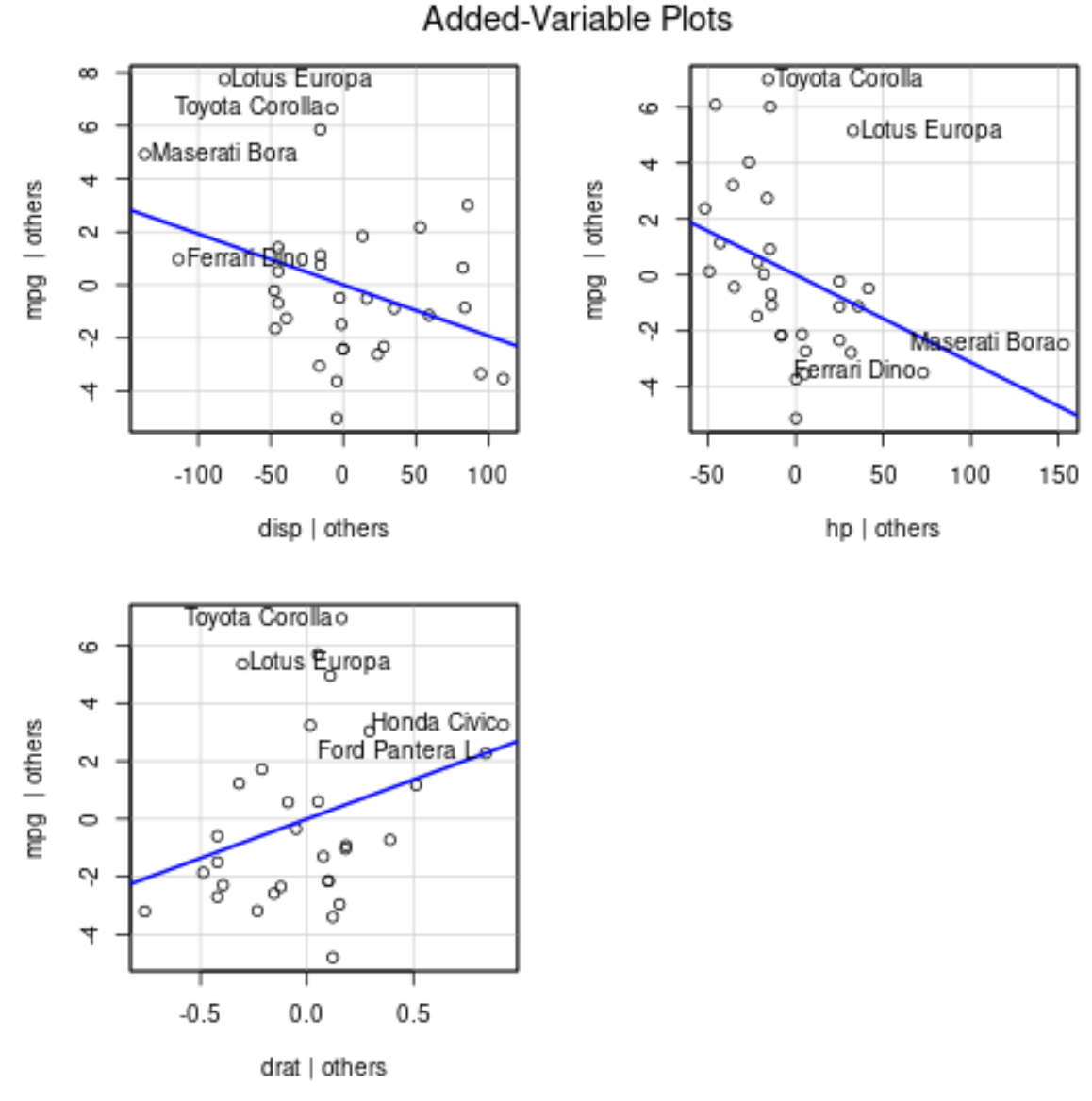
Oto jak interpretować każdy wykres:

• Oś x wyświetla pojedynczą zmienną predykcyjną, a oś y wyświetla zmienną odpowiedzi.
• Niebieska linia pokazuje powiązanie między zmienną predykcyjną a zmienną odpowiedzi, przy jednoczesnym zachowaniu wartości wszystkich pozostałych zmiennych predykcyjnych na stałym poziomie .
• Oznaczone punkty na każdym wykresie reprezentują 2 obserwacje z największymi resztami i 2 obserwacje z największą dźwignią częściową.

Należy zauważyć, że kąt linii na każdym wykresie odpowiada znakowi współczynnika oszacowanego równania regresji.

Oto na przykład oszacowane współczynniki dla każdej zmiennej predykcyjnej w modelu:

• wyświetlacz: -0.019232
• rozdz.: -0,031229
• data: 2.714975

Należy zauważyć, że kąt linii jest dodatni na dodanym wykresie zmiennych dla drat , natomiast jest ujemny dla disp i hp , co odpowiada znakom ich oszacowanych współczynników:

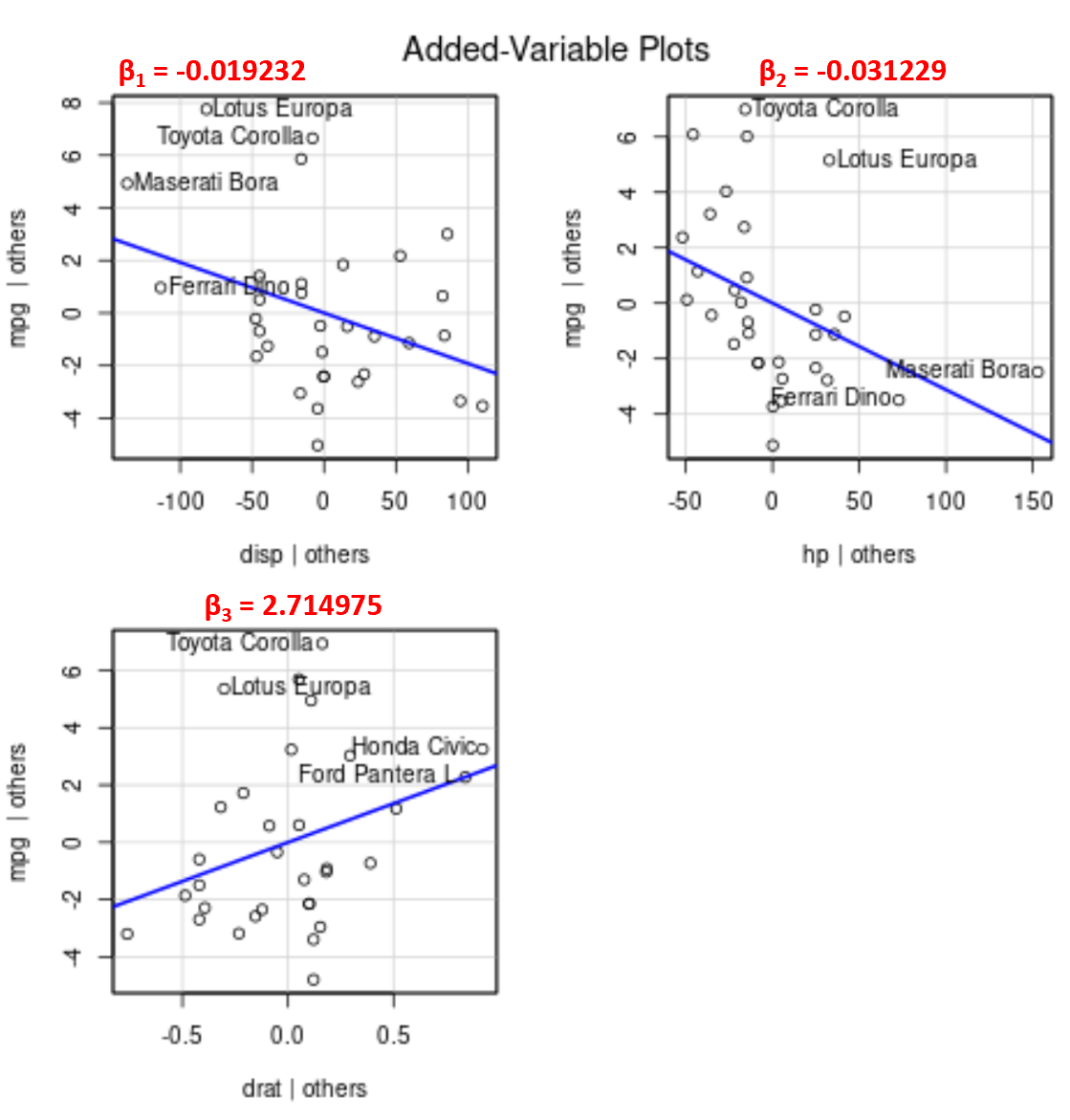
Chociaż nie możemy wykreślić pojedynczej dopasowanej linii regresji na wykresie 2D, ponieważ mamy wiele zmiennych predykcyjnych, te dodane wykresy zmiennych pozwalają nam obserwować związek między każdą indywidualną zmienną predykcyjną a zmienną odpowiedzi, przy jednoczesnym zachowaniu pozostałych zmiennych predykcyjnych na stałym poziomie.