Czy wynik z-score może być ujemny?

W statystyce wynik z informuje nas, o ile odchyleń standardowych dana wartość znajduje się od średniej . Do obliczenia wskaźnika Z używamy następującego wzoru:

z = (X – μ) / σ

gdzie X to wartość, którą analizujemy, μ to średnia, a σ to odchylenie standardowe.

Wynik A może być dodatni, ujemny lub zerowy.

Dodatni wynik z wskazuje, że dana wartość jest powyżej średniej, ujemny wynik z wskazuje, że dana wartość jest poniżej średniej, a wynik az wynoszący zero oznacza, że dana wartość jest równa średniej.

Kilka przykładów powinno to wyjaśnić.

Przykłady: Obliczanie wyniku Z

Załóżmy, że mamy następujący zbiór danych pokazujący wysokość (w calach) określonej grupy roślin:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

Średnia próbki tego zbioru danych wynosi 13 , a odchylenie standardowe próbki wynosi 5,51 .

1. Znajdź wynik z dla wartości „8” w tym zbiorze danych.

Oto jak obliczyć wskaźnik Z:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Oznacza to, że wartość „8” jest o 0,91 odchylenia standardowego niższa od średniej.

2. Znajdź wynik z dla wartości „13” w tym zbiorze danych.

Oto jak obliczyć wskaźnik Z:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Oznacza to, że wartość „13” jest dokładnie równa średniej.

3. Znajdź wynik z dla wartości „20” w tym zbiorze danych.

Oto jak obliczyć wskaźnik Z:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Oznacza to, że wartość „20” jest o 1,28 odchylenia standardowego powyżej średniej.

Jak interpretować wyniki Z

Wykres AZ mówi nam, jaki procent wartości spada poniżej określonych wyników Z. Kilka przykładów powinno to wyjaśnić.

Przykład 1: Ujemne wyniki Z

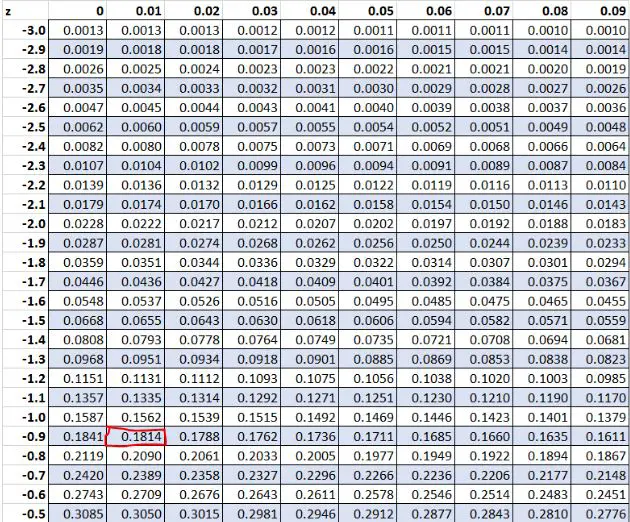
Wcześniej odkryliśmy, że surowa wartość „8” w naszym zbiorze danych miała wynik z wynoszący -0,91 . Według tabeli Z 18,14% wartości jest niższych od tej wartości.

Przykład 2: Wyniki Z równe zeru

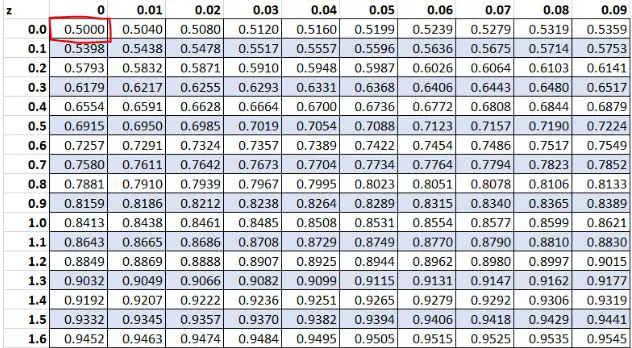
Wcześniej odkryliśmy, że surowa wartość „13” w naszym zbiorze danych miała współczynnik z wynoszący 0 . Według tabeli Z 50,00% wartości jest mniejszych od tej wartości.

Przykład 3: Pozytywne wyniki Z

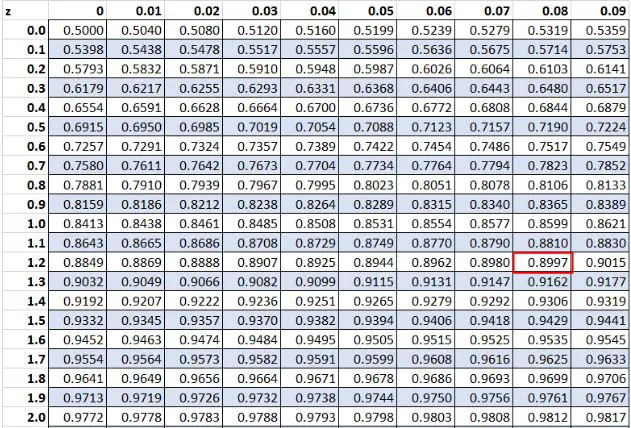
Wcześniej odkryliśmy, że surowa wartość „20” w naszym zbiorze danych miała wynik z wynoszący 1,28 . Według tabeli Z 89,97% wartości jest niższych od tej wartości.

Wniosek

Wyniki Z mogą przyjmować dowolną wartość pomiędzy ujemną nieskończonością a dodatnią nieskończonością, ale większość wyników Z mieści się w granicach 2 odchyleń standardowych od średniej. W statystyce istnieje zasada zwana praktyczną zasadą , która stwierdza, że dla danego zbioru danych o rozkładzie normalnym:

• 68% wartości danych mieści się w obrębie jednego odchylenia standardowego średniej.
• 95% wartości danych mieści się w granicach dwóch odchyleń standardowych od średniej.
• 99,7% wartości danych mieści się w trzech odchyleniach standardowych od średniej.

Im wyższa wartość bezwzględna wyniku z, tym bardziej surowa wartość jest oddalona od średniej zbioru danych. Im niższa wartość bezwzględna wyniku z, tym wartość surowa jest bliższa średniej zbioru danych.

Powiązane tematy:

Zasady kalkulatora kciuka
Jak zastosować regułę praktyczną w programie Excel