Co to jest zmodyfikowany wynik z? (definicja – przykład)

W statystyce wynik z informuje nas, o ile odchyleń standardowych dana wartość znajduje się od średniej . Do obliczenia wskaźnika Z używamy następującego wzoru:

Wynik Z = (x _i – μ) / σ

Złoto:

• x _i : pojedyncza wartość danych
• μ: średnia ze zbioru danych
• σ: odchylenie standardowe zbioru danych

Wyniki Z są często używane do wykrywania wartości odstających w zbiorze danych. Na przykład obserwacje z wynikiem z mniejszym niż -3 lub większym niż 3 są często uważane za wartości odstające.

Jednak na wynik Z mogą mieć wpływ wyjątkowo duże lub małe wartości danych. Dlatego też skuteczniejszym sposobem wykrywania wartości odstających jest użycie zmodyfikowanego wskaźnika Z , obliczonego w następujący sposób:

Zmodyfikowany wynik z = 0,6745 (x _i – x̃) / MAD

Złoto:

• x _i : pojedyncza wartość danych
• x̃: Mediana zbioru danych
• MAD: mediana bezwzględnego odchylenia zbioru danych

Zmodyfikowany wynik Z jest bardziej niezawodny, ponieważ do obliczenia wyników Z wykorzystuje się medianę, a nie średnią, na którą wpływają wartości odstające .

Iglewicz i Hoaglin zalecają, aby wartości ze zmodyfikowanymi wynikami Z mniejszymi niż -3,5 lub większymi niż 3,5 były oznaczone jako potencjalne wartości odstające.

Poniższy przykład pokazuje krok po kroku, jak obliczyć zmodyfikowane wyniki Z dla danego zestawu danych.

Krok 1: Utwórz dane

Załóżmy, że mamy następujący zbiór danych zawierający 16 wartości:

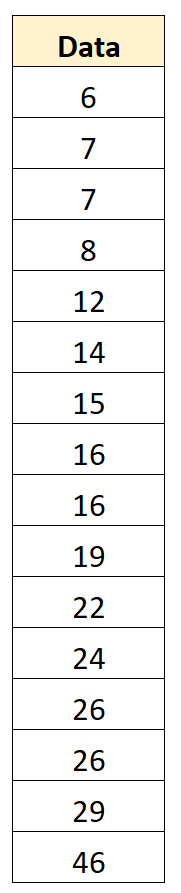
Krok 2: Znajdź medianę

Następnie znajdziemy medianę. Stanowi to punkt środkowy zbioru danych, który okazuje się wynosić 16 .

Krok 3: Znajdź bezwzględną różnicę między każdą wartością a medianą

Następnie znajdziemy bezwzględną różnicę między każdą indywidualną wartością danych a medianą. Na przykład bezwzględną różnicę między pierwszą wartością danych a medianą oblicza się w następujący sposób:

Różnica bezwzględna = |6 – 16| = 10

Możemy użyć tego samego wzoru do obliczenia bezwzględnej różnicy między każdą indywidualną wartością danych a medianą:

Krok 4: Znajdź bezwzględne odchylenie mediany

Następnie znajdziemy bezwzględne odchylenie mediany. To jest mediana drugiej kolumny, która okazuje się wynosić 8 .

Krok 5: Znajdź zmodyfikowany wynik Z dla każdej wartości danych

Na koniec możemy obliczyć zmodyfikowany wynik Z dla każdej wartości danych, korzystając z następującego wzoru:

Zmodyfikowany wynik z = 0,6745 (x _i – x̃) / MAD

Na przykład zmodyfikowany wynik z dla pierwszej wartości danych oblicza się w następujący sposób:

Zmodyfikowany wynik z = 0,6745*(6-16) / 8 = -0,843

Możemy powtórzyć tę formułę dla każdej wartości w zbiorze danych:

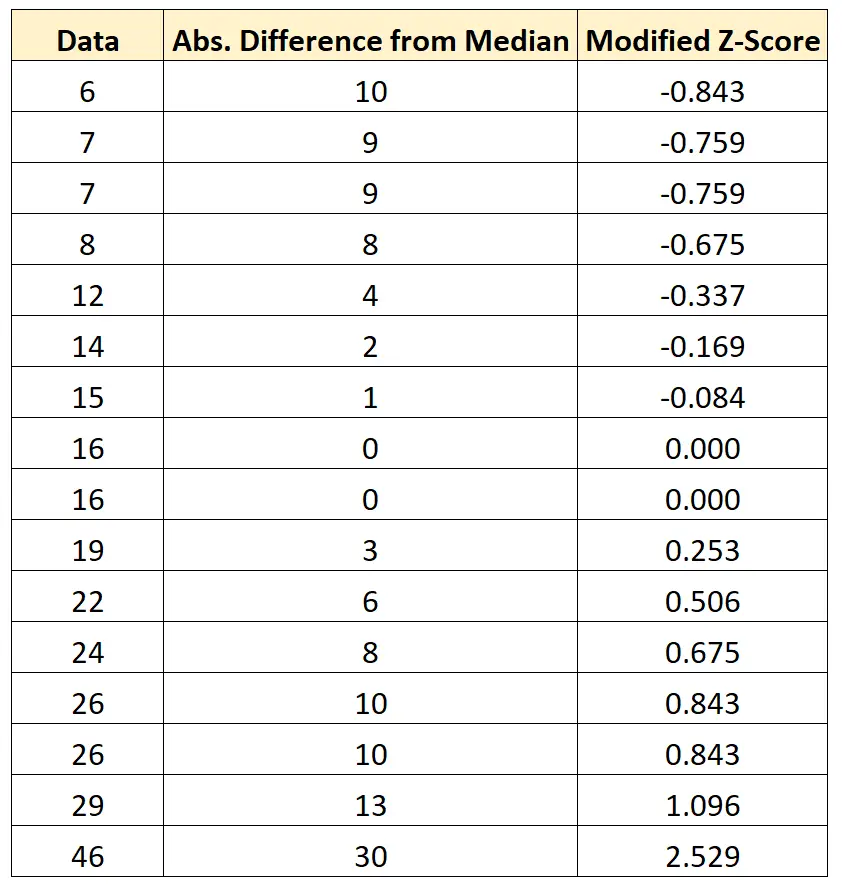
Widzimy, że żadna wartość w zbiorze danych nie ma zmodyfikowanego wyniku z-score mniejszego niż -3,5 lub większego niż 3,5, dlatego nie oznaczamy żadnej wartości w tym zbiorze danych jako potencjalnej wartości odstającej.

Jak postępować z wartościami odstającymi

Jeśli w Twoim zbiorze danych występuje wartość odstająca, masz kilka możliwości:

• Upewnij się, że wartość odstająca nie jest wynikiem błędu we wprowadzaniu danych. Czasami osoba po prostu wprowadza niewłaściwą wartość danych podczas zapisywania danych. Jeśli występuje wartość odstająca, najpierw sprawdź, czy wartość została wprowadzona poprawnie i czy nie jest to błąd.
• Przypisz nową wartość do wartości odstającej . Jeśli okaże się, że wartość odstająca wynika z błędu we wprowadzaniu danych, możesz zdecydować się na przypisanie jej nowej wartości, takiej jak średnia lub mediana zbioru danych.
• Usuń wartość odstającą. Jeśli wartość rzeczywiście odbiega od normy, możesz ją usunąć, jeśli będzie miała znaczący wpływ na ogólną analizę. Pamiętaj tylko, aby wspomnieć w raporcie końcowym lub analizie, że usunąłeś wartość odstającą.