Jak wyodrębnić reszty z funkcji lm() w r

Aby wyodrębnić reszty z funkcji lm() w R, możesz użyć następującej składni:

 fit$residuals

W tym przykładzie założono, że użyliśmy funkcji lm() w celu dopasowania modelu regresji liniowej i nazwaliśmy wyniki dopasowaniem .

Poniższy przykład pokazuje, jak zastosować tę składnię w praktyce.

Powiązane: Jak wyodrębnić wartość R-kwadrat z funkcji lm() w języku R

Przykład: Jak wyodrębnić reszty z lm() w R

Załóżmy, że mamy następującą ramkę danych w R, która zawiera informacje o rozegranych minutach, sumie fauli i sumie punktów zdobytych przez 10 koszykarzy:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

Załóżmy, że chcemy dopasować następujący model regresji liniowej:

punkty = β ₀ + β ₁ (minuty) + β ₂ (faule)

Możemy użyć funkcji lm(), aby dopasować ten model regresji:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

Następnie możemy wpisać fit$residuals, aby wyodrębnić reszty z modelu:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

Ponieważ w naszej bazie danych było łącznie 10 obserwacji, istnieje 10 reszt – po jednej dla każdej obserwacji.

Na przykład:

• Pierwsza obserwacja ma resztę 2089 .
• Druga obserwacja ma resztę -0,798 .
• Trzecia obserwacja ma resztę 0,637 .

I tak dalej.

Możemy następnie utworzyć wykres reszt w stosunku do dopasowanych wartości, jeśli chcemy:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

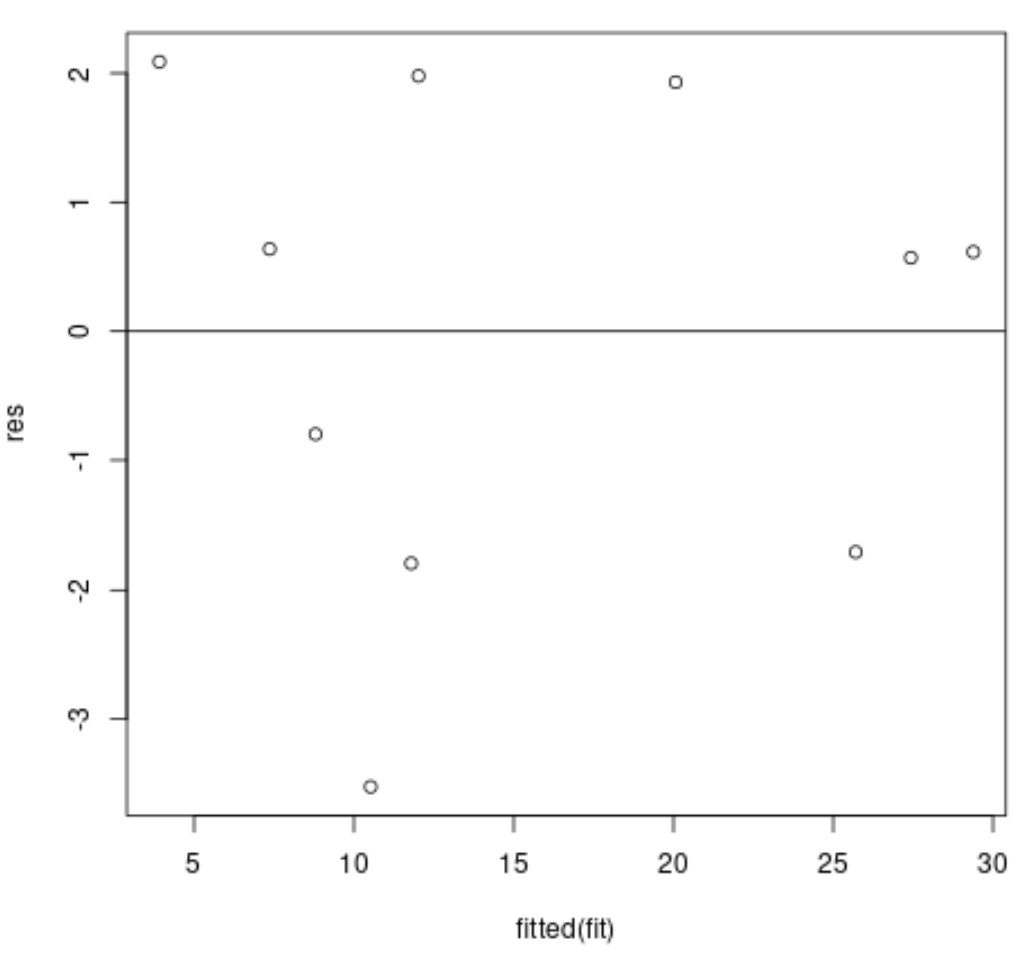
Oś x wyświetla dopasowane wartości, a oś y wyświetla reszty.

W idealnym przypadku reszty powinny być losowo rozrzucone wokół zera, bez wyraźnego wzoru, aby zapewnić spełnienie założenia o homoskedastyczności .

Na powyższym wykresie reszt widać, że reszty wydają się być losowo rozproszone wokół zera, bez wyraźnego wzoru, co oznacza, że założenie o homoskedastyczności jest prawdopodobnie spełnione.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w języku R:

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak utworzyć wykres rezydualny w R