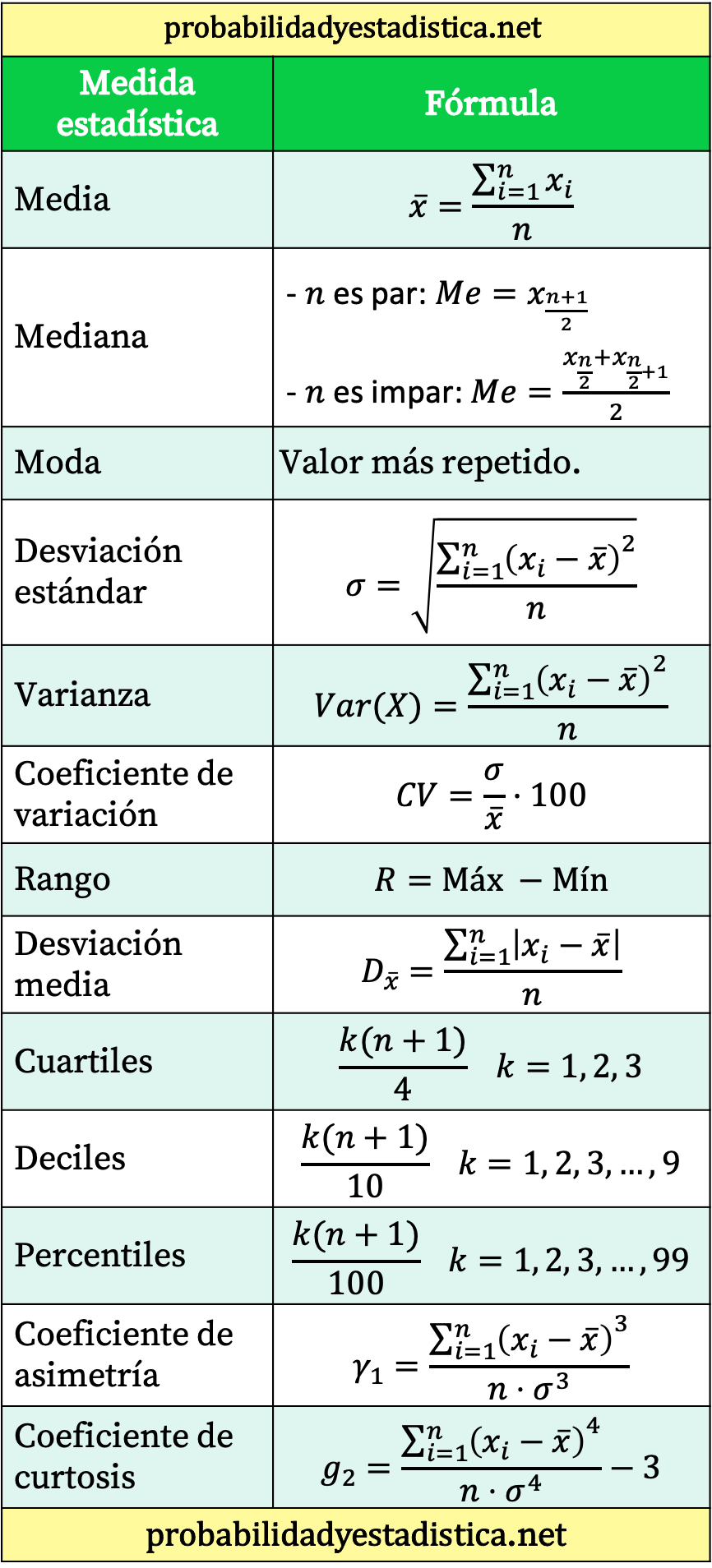
Wzory statystyczne

Przez Benjamin Anderson 1 sierpnia, 2023 Statystyka 0 komentarzy

Tutaj znajdziesz główne wzory statystyczne. Pozostawiamy również linki do naszych artykułów, w których można zobaczyć przykłady zastosowania poszczególnych wzorów statystycznych, a ponadto można skorzystać z kalkulatora online, aby nie musieć wykonywać obliczeń i znać bezpośrednio wynik wzoru.

Wzory na statystyczne miary tendencji centralnej

Połowa

Aby obliczyć średnią, dodaj wszystkie wartości, a następnie podziel przez całkowitą liczbę danych. Wzór na średnią jest zatem następujący:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

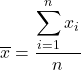
W statystyce średnia jest również nazywana średnią arytmetyczną lub średnią .

➤ Zobacz: Kalkulator średniej arytmetycznej

Mediana

Mediana to środkowa wartość wszystkich danych uporządkowanych od najmniejszej do największej. Innymi słowy, mediana dzieli uporządkowany zbiór danych na dwie równe części.

Obliczenie mediany zależy od tego, czy łączna liczba danych jest parzysta czy nieparzysta:

Jeśli całkowita liczba danych jest nieparzysta , medianą będzie wartość mieszcząca się w samym środku danych. To znaczy wartość znajdująca się na pozycji (n+1)/2 posortowanych danych.

$Me=x_{\frac{n+1}{2}$

Jeśli całkowita liczba punktów danych jest parzysta , mediana będzie średnią z dwóch punktów danych znajdujących się w środku. Oznacza to średnią arytmetyczną wartości znajdujących się na pozycjach n/2 i n/2+1 uporządkowanych danych.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Złoto

$n$

oznacza całkowitą liczbę danych w próbie, a symbol Me oznacza medianę.

➤ Zobacz: Kalkulator mediany

Moda

W statystyce tryb to wartość w zbiorze danych, która ma najwyższą częstotliwość bezwzględną, to znaczy tryb jest najczęściej powtarzaną wartością w zbiorze danych.

Dlatego nie ma konkretnego wzoru na modę, ale aby obliczyć mod zbioru danych statystycznych, wystarczy policzyć, ile razy każdy element danych pojawia się w próbce, a dane będą najczęściej powtarzane.

Tryb można również nazwać trybem statystycznym lub wartością modalną .

➤ Zobacz: Kalkulator mody

Wzory na statystyczne miary dyspersji

Odchylenie standardowe

Odchylenie standardowe, zwane także odchyleniem standardowym, jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń serii danych podzielonej przez całkowitą liczbę obserwacji.

Zatem wzór na odchylenie standardowe wygląda następująco:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Zobacz: Kalkulator odchylenia standardowego

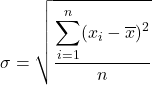
Zmienność

Wariancja jest równa sumie kwadratów reszt z całkowitej liczby obserwacji. Wzór na tę metrykę statystyczną jest zatem następujący:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Złoto:

$X$

jest zmienną losową, dla której chcesz obliczyć wariancję.
$x_i$

jest wartością danych

$i$

.
$n$

to całkowita liczba obserwacji.
$\overline{X}$

jest średnią zmiennej losowej

$X$

.

➤ Zobacz: Kalkulator luki

Współczynnik zmienności

W statystyce współczynnik zmienności jest miarą rozproszenia stosowaną do określenia rozproszenia zbioru danych w stosunku do jego średniej. Współczynnik zmienności oblicza się, dzieląc odchylenie standardowe danych przez jego średnią, a następnie mnożąc przez 100, aby wyrazić wartość w procentach.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Zobacz: Kalkulator współczynnika zmienności

Czysty

Rozstęp statystyczny jest miarą rozproszenia, która wskazuje różnicę między wartością maksymalną a minimalną wartością danych w próbce. Dlatego też, aby obliczyć wielkość populacji lub próby statystycznej, od wartości minimalnej należy odjąć wartość maksymalną.

$R=\text{M\'ax}-\text{M\'in}$

➤ Zobacz: Przykład zakresu statystycznego

Zakres międzykwartylowy

Rozstęp międzykwartylowy , zwany także rozstępem międzykwartylowym , jest miarą rozproszenia statystycznego, która wskazuje różnicę między trzecim i pierwszym kwartylem.

Dlatego, aby obliczyć rozstęp międzykwartylowy zbioru danych statystycznych, należy najpierw znaleźć trzeci i pierwszy kwartyl, a następnie je odjąć.

$IQR=Q_3-Q_1$

➤ Zobacz: Kalkulator rozstępu międzykwartylowego

średnia różnica

Średnie odchylenie , zwane także średnim odchyleniem bezwzględnym , jest średnią odchyleń bezwzględnych. Średnie odchylenie jest zatem równe sumie odchyleń każdego elementu danych od średniej arytmetycznej podzielonej przez całkowitą liczbę elementów danych.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Zobacz: Kalkulator odchylenia średniego

Wzory na statystyczne pomiary położenia

kwartyle

W statystyce kwartyle to trzy wartości dzielące zbiór uporządkowanych danych na cztery równe części. Zatem pierwszy, drugi i trzeci kwartyl reprezentuje odpowiednio 25%, 50% i 75% wszystkich danych statystycznych.

Kwartyle są reprezentowane przez dużą literę Q i indeks kwartylowy, więc pierwszy kwartyl to Q ₁ , drugi kwartyl to Q ₂ , a trzeci kwartyl to Q ₃ .

Wzór kwartylowy to:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Uwaga: ten wzór informuje nas o pozycji kwartyla, a nie o jego wartości. Kwartylem będą dane znajdujące się na pozycji otrzymanej ze wzoru.

Czasami jednak wynik tej formuły da nam liczbę dziesiętną. Musimy zatem rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:

Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , kwartylem jest dana, która znajduje się na pozycji określonej we wzorze powyżej.
Jeżeli wynikiem wzoru jest liczba zawierająca część dziesiętną , wartość kwartylowa obliczana jest według następującego wzoru:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Gdzie x _i oraz x _i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.

➤ Zobacz: Kalkulator kwartylowy

decyle

W statystyce decyle to dziewięć wartości, które dzielą zbiór uporządkowanych danych na dziesięć równych części. Tak więc pierwszy, drugi, trzeci… decyl reprezentuje 10%, 20%, 30%… próbki lub populacji.

Decyle są reprezentowane przez wielką literę D i indeks decylowy, to znaczy pierwszy decyl to D ₁ , drugi decyl to D ₂ , trzeci decyl to D ₃ itd.

Wzór na decyl jest następujący:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Uwaga: ten wzór informuje nas o pozycji decyla, a nie o jego wartości. Decylem będą dane znajdujące się na pozycji otrzymanej ze wzoru.

Czasami jednak wynik tej formuły da nam liczbę dziesiętną, dlatego musimy rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:

Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , decylem jest dana znajdująca się na pozycji określonej we wzorze powyżej.
Jeżeli wynikiem wzoru jest liczba zawierająca część dziesiętną , wartość decyla oblicza się według następującego wzoru:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Gdzie x _i oraz x _i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.

➤ Zobacz: Kalkulator decyli

percentyle

W statystyce percentyle to wartości dzielące zbiór uporządkowanych danych na sto równych części. Zatem percentyl wskazuje wartość, poniżej której spada procent zbioru danych.

Percentyle są reprezentowane przez wielką literę P i indeks percentyla, czyli pierwszy percentyl to P ₁ , 40. percentyl to P ₄₀ , 79. percentyl to P ₇₉ itd.

Wzór percentyla to:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Uwaga: ten wzór informuje nas o położeniu percentyla, ale nie o jego wartości. Percentylem będą dane znajdujące się na pozycji uzyskanej ze wzoru.

Czasami jednak wynik tej formuły da nam liczbę dziesiętną, dlatego musimy rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:

Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , percentylowi odpowiadają dane znajdujące się na pozycji podanej we wzorze powyżej.
Jeśli wynikiem wzoru jest liczba z częścią dziesiętną , dokładna wartość percentyla jest obliczana przy użyciu następującego wzoru:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Gdzie x _i oraz x _i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.

➤ Zobacz: Kalkulator percentyla

Statystyczne wzory na pomiar kształtu

współczynnik asymetrii

Współczynnik skośności lub wskaźnik skośności to współczynnik statystyczny używany do określenia skośności rozkładu. Zatem obliczając współczynnik asymetrii, można poznać rodzaj asymetrii rozkładu bez konieczności tworzenia jej graficznej reprezentacji.

Wzór na współczynnik asymetrii jest następujący:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Równoważnie do obliczenia współczynnika asymetrii Fishera można zastosować jeden z dwóch poniższych wzorów:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

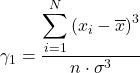
Złoto

$E$

jest oczekiwaniem matematycznym,

$\overline{x}$

średnia arytmetyczna,

$\sigma$

odchylenie standardowe i

$n$

całkowita liczba danych.

➤ Zobacz: Współczynnik asymetrii

współczynnik kurtozy

Kurtoza, zwana także ostrością, wskazuje, jak skoncentrowany jest rozkład wokół średniej. Innymi słowy, kurtoza wskazuje, czy rozkład jest stromy czy płaski. W szczególności im większa kurtoza rozkładu, tym jest ona bardziej stroma (lub ostrzejsza).

Wzór na współczynnik kurtozy jest następujący:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

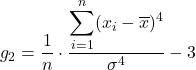
Złoto

$x_i$

jest wartością odpowiadającą obserwacji

$i$

$\overline{x}$

średnia arytmetyczna,

$\sigma$

odchylenie standardowe i

$n$

całkowita liczba danych.

➤ Zobacz: Kalkulator współczynnika spłaszczenia

Tabela podsumowująca wszystkie formuły statystyczne

Na koniec zostawiamy tabelę podsumowującą główne formuły statystyczne.

➤ Zobacz: Wzory na prawdopodobieństwo

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Wzory na statystyczne miary tendencji centralnej

Połowa

Mediana

Moda

Wzory na statystyczne miary dyspersji

Odchylenie standardowe

Zmienność

Współczynnik zmienności

Czysty

Zakres międzykwartylowy

średnia różnica

Wzory na statystyczne pomiary położenia

kwartyle

decyle

percentyle

Statystyczne wzory na pomiar kształtu

współczynnik asymetrii

współczynnik kurtozy

Tabela podsumowująca wszystkie formuły statystyczne

o autorze

Dr Benjamin Anderson

Dodaj komentarz