Jak obliczyć wyniki z w spss

Wynik z mówi nam, ile odchyleń standardowych dana wartość ma od średniej.

Wynik z danej wartości oblicza się w następujący sposób:

wynik z = (x – μ) / σ

Złoto:

• x: wartość indywidualna
• μ: średnia populacji
• σ: odchylenie standardowe populacji

W tym samouczku wyjaśniono, jak obliczyć wyniki Z w SPSS.

Powiązane: Jak interpretować wyniki Z

Jak obliczyć wyniki Z w SPSS

Załóżmy, że mamy następujący zbiór danych, który pokazuje roczny dochód (w tysiącach) 15 osób:

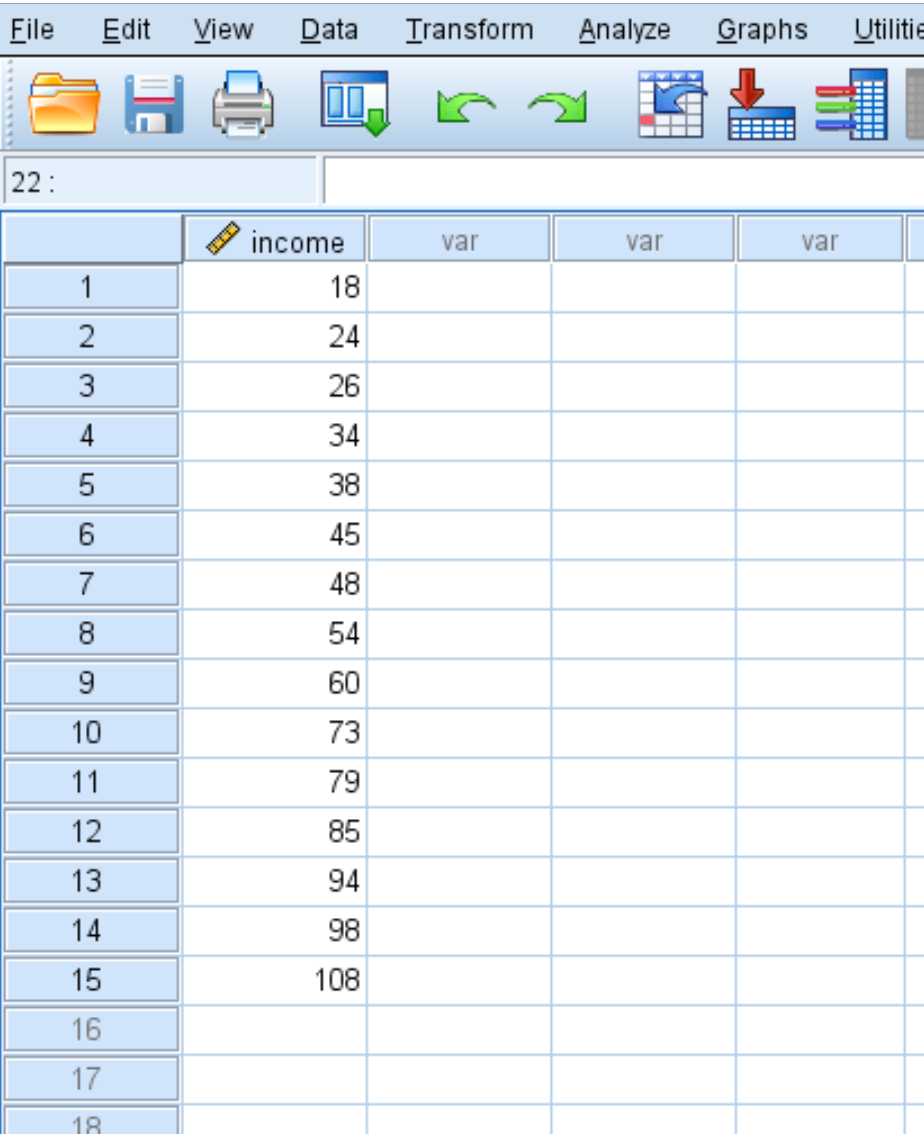
Aby obliczyć współczynniki Z dla każdej wartości w zbiorze danych, kliknij kartę Analiza , następnie Statystyki opisowe , a następnie Elementy opisowe :

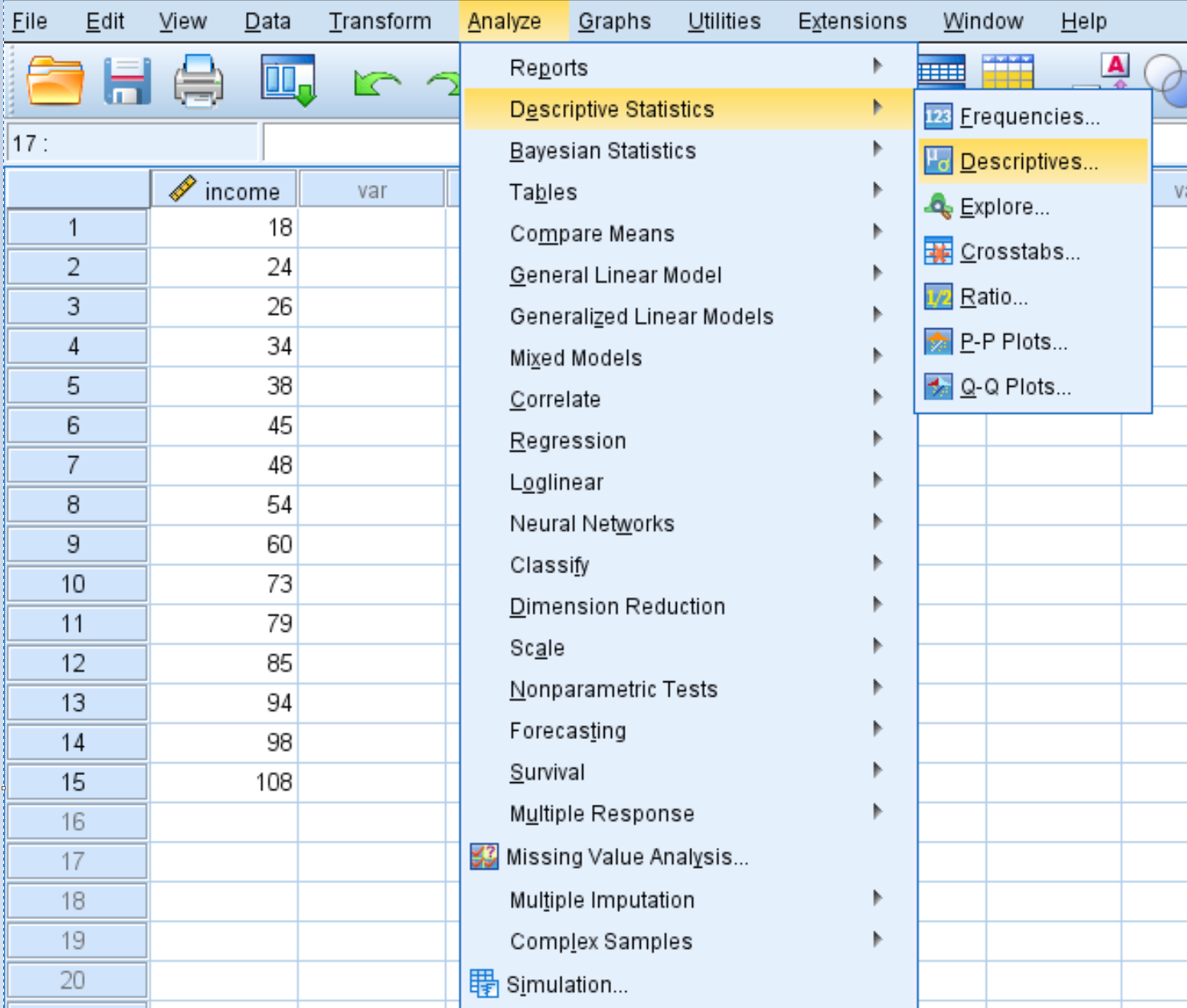
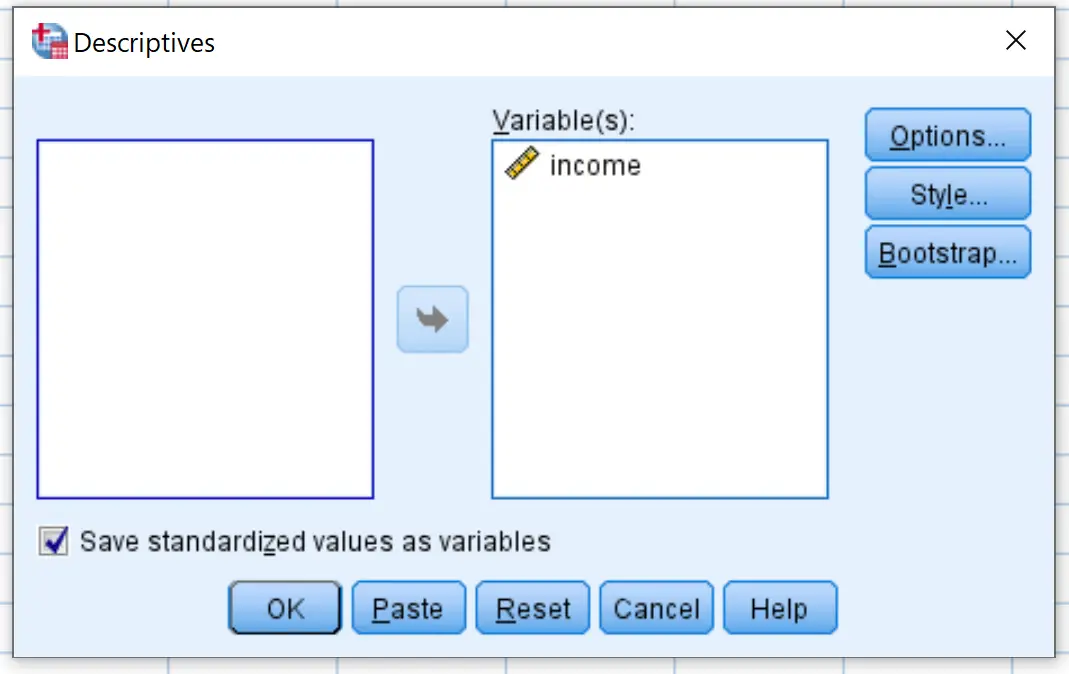
W nowym oknie, które się pojawi, przeciągnij zmienną dochodu do pola o nazwie Zmienne.

Upewnij się, że pole obok Zapisz standardowe wartości jako zmienne jest zaznaczone, a następnie kliknij OK .

Po kliknięciu przycisku OK SPSS utworzy tabelę statystyk opisowych dla Twojego zbioru danych:

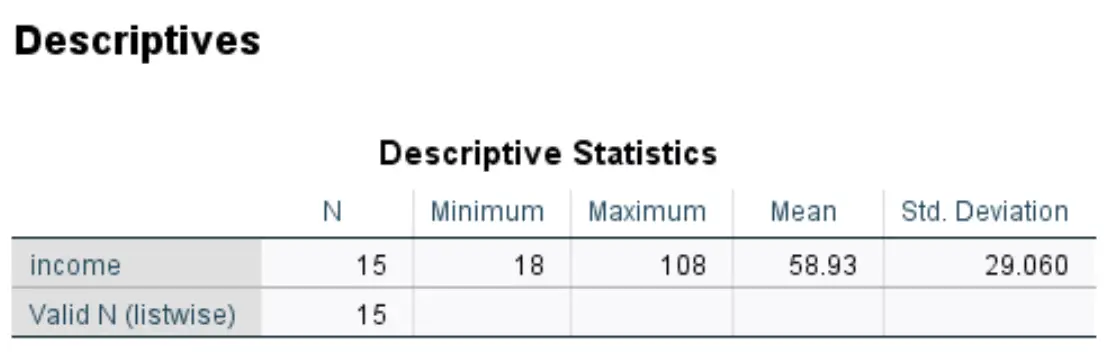
SPSS utworzy także nową kolumnę wartości, która wyświetli wynik Z dla każdej z oryginalnych wartości w zestawie danych:

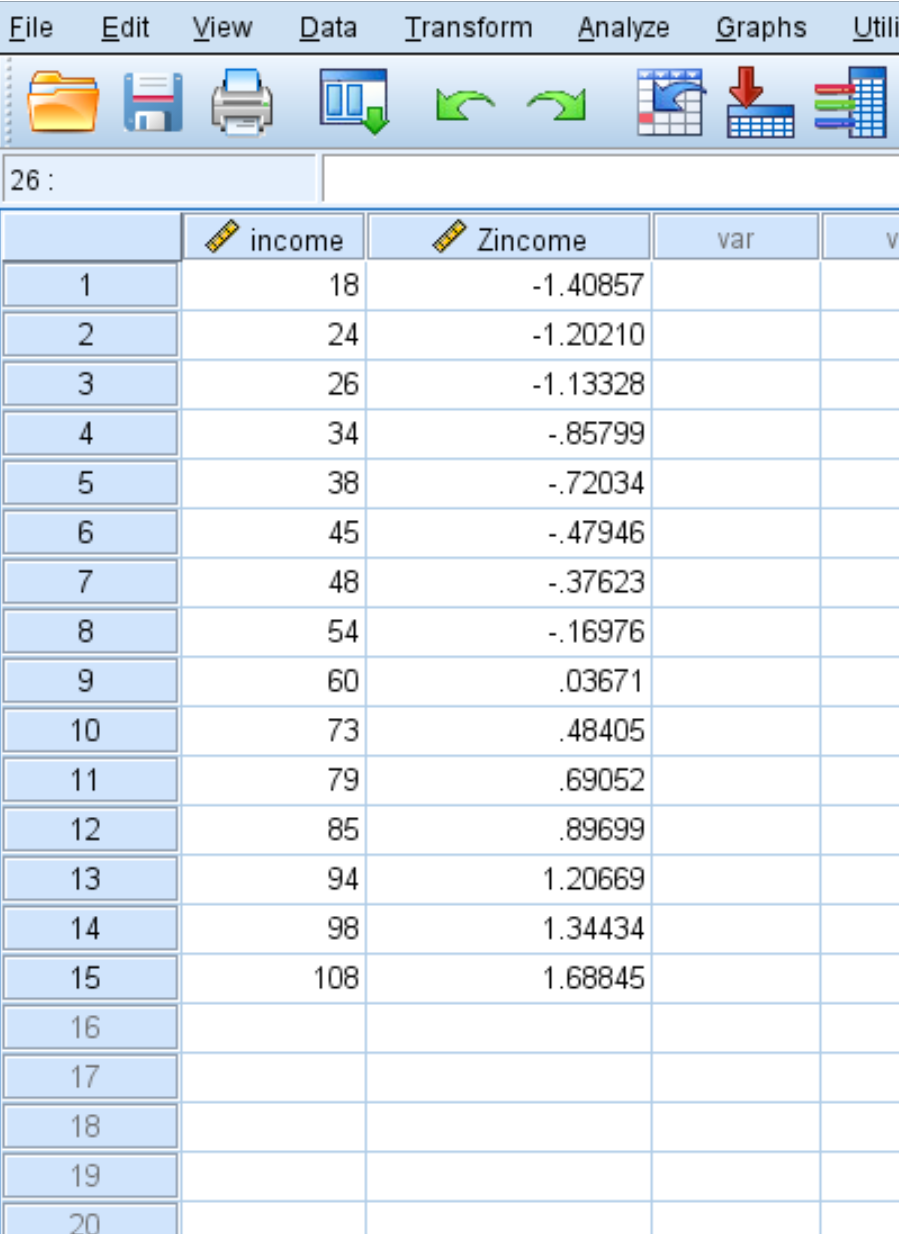
Każdy z wyników z jest obliczany przy użyciu wzoru z = (x – μ) / σ

Na przykład wynik Z dla wartości dochodu wynoszącej 18 wynosi:

z = (18 – 58,93) / 29,060 = -1,40857 .

Wyniki Z dla wszystkich innych wartości danych są obliczane w ten sam sposób.

Jak interpretować wyniki Z

Pamiętaj, że wynik z mówi nam po prostu, ile odchyleń standardowych dana wartość ma od średniej.

Wynik A może być dodatni, ujemny lub równy zero:

• Dodatni wynik Z wskazuje, że dana wartość jest powyżej średniej.
• Ujemny wynik Z wskazuje, że dana wartość jest poniżej średniej.
• Wynik Z wynoszący zero oznacza, że dana wartość jest równa średniej.

W naszym przykładzie odkryliśmy, że średnia wyniosła 58,93, a odchylenie standardowe 29,060.

Tak więc pierwszą wartością w naszym zbiorze danych było 18, co dało wynik z wynoszący (18 – 58,93) / 29,060 = -1,40857 .

Oznacza to, że wartość „18” jest o 1,40857 odchylenia standardowego niższa od średniej.

I odwrotnie, ostatnia wartość w naszych danych wynosiła 108, co odpowiadało wynikowi Z wynoszącemu (108 – 58,93) / 29,060 = 1,68845 .

Oznacza to, że wartość „108” jest o 1,68845 odchylenia standardowego powyżej średniej.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SPSS:

Jak obliczyć statystyki opisowe dla zmiennych w SPSS
Jak obliczyć pięciocyfrowe podsumowanie w SPSS
Jak zidentyfikować wartości odstające w SPSS