Jak utworzyć krzywą roc w sas
Regresja logistyczna to metoda, której możemy użyć do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna.
Aby ocenić, jak dobrze model regresji logistycznej pasuje do zbioru danych, możemy przyjrzeć się następującym dwóm metrykom:
- Czułość: prawdopodobieństwo, że model przewiduje pozytywny wynik obserwacji, gdy wynik jest rzeczywiście pozytywny. Nazywa się to również „prawdziwie dodatnią stopą procentową”.
- Specyficzność: prawdopodobieństwo, że model przewiduje negatywny wynik obserwacji, gdy wynik jest faktycznie negatywny. Nazywa się to również „prawdziwie ujemną stopą”.
Jednym ze sposobów wizualizacji tych dwóch pomiarów jest utworzenie krzywej ROC , która oznacza krzywą „charakterystyki działania odbiornika”. To jest wykres przedstawiający czułość i swoistość modelu regresji logistycznej.
Poniższy przykład pokazuje krok po kroku, jak utworzyć i zinterpretować krzywą ROC w SAS-ie.
Krok 1: Utwórz zbiór danych
Najpierw utworzymy zbiór danych zawierający informacje o następujących zmiennych dla 18 uczniów:
- Przyjęcie na określoną uczelnię (1 = tak, 0 = nie)
- GPA (skala od 1 do 4)
- Wynik ACT (skala od 1 do 36)
/*create dataset*/ data my_data; input acceptance gpa act; datalines ; 1 3 30 0 1 21 0 2 26 0 1 24 1 3 29 1 3 34 0 3 31 1 2 29 0 1 21 1 2 21 0 1 15 1 3 32 1 4 31 1 4 29 0 1 24 1 4 29 1 3 21 1 4 34 ; run ;
Krok 2: Dopasuj model regresji logistycznej i utwórz krzywą ROC
Następnie użyjemy logistyki proc , aby dopasować model regresji logistycznej, używając „akceptacji” jako zmiennej odpowiedzi oraz „gpa” i „działania” jako zmiennych predykcyjnych.
Określimy zmniejszanie , aby SAS wiedział, jak przewidzieć prawdopodobieństwo, że zmienna odpowiedzi przyjmie wartość 1.
Użyjemy również plots(only)=roc do utworzenia krzywej ROC dla modelu:
/*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
model acceptance = gpa act;
run ;
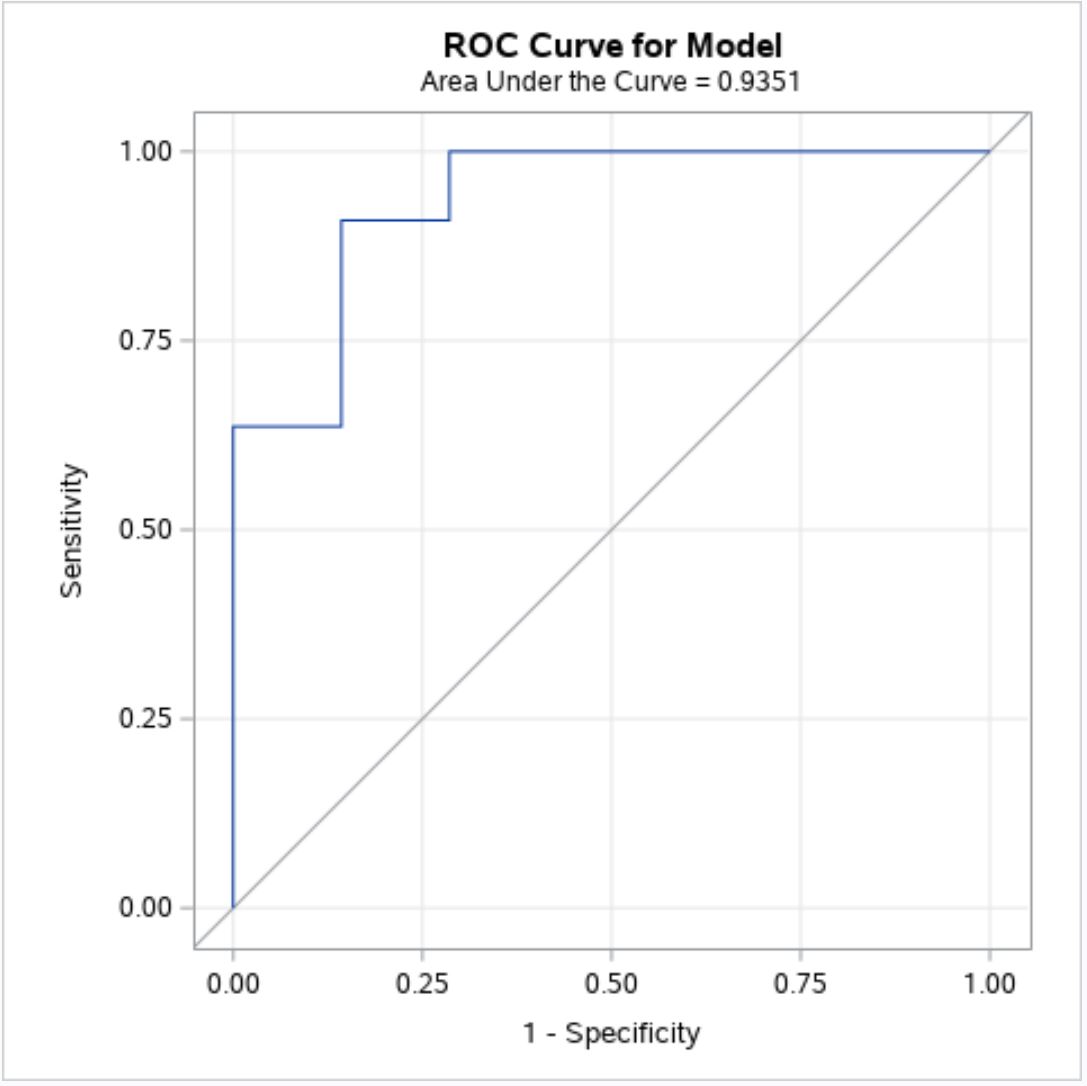
Krok 3: Zinterpretuj krzywą ROC
Im bardziej krzywa ROC pasuje do lewego górnego rogu wykresu, tym lepiej model przewiduje wartość wartości odpowiedzi w zbiorze danych.
Z powyższego wykresu widzimy, że niebieska krzywa ROC ma tendencję do przylegania do lewego górnego rogu, co wskazuje, że model regresji logistycznej dobrze radzi sobie z przewidywaniem wartości wartości odpowiedzi.
Aby określić ilościowo, jak dobrze model regresji logistycznej pasuje do danych, możemy obliczyć AUC – obszar pod krzywą – który mówi nam, jaka część wykresu znajduje się pod krzywą.
Im AUC jest bliższe 1, tym lepszy model. Model z AUC równym 0,5 nie jest lepszy od modelu przeprowadzającego losową klasyfikację.
Pod tytułem wykresu powyżej widzimy, że AUC tego modelu wynosi 0,9351 .
Ponieważ wartość ta jest bliska jedności, potwierdza to, że model dobrze przewiduje wartość wartości odpowiedzi.
Możemy również użyć wartości AUC do porównania dopasowania różnych modeli regresji logistycznej.
Załóżmy na przykład, że dopasowujemy dwa różne modele regresji logistycznej i obliczamy wartości AUC dla każdego z nich:
- AUC modelu 1: 0,9351
- AUC modelu 2: 0,8140
Ponieważ AUC Modelu 1 jest większe, mówi nam to, że Model 1 lepiej dopasowuje dane niż Model 2.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje w SAS-ie:
Jak wykonać prostą regresję liniową w SAS-ie
Jak wykonać wielokrotną regresję liniową w SAS-ie
Jak przeprowadzić regresję logistyczną w SAS-ie