Jak interpretować zakrzywiony wykres resztowy (z przykładem)

Wykresy reszt służą do oceny, czy reszty modelu regresji mają rozkład normalny i czy wykazują heteroskedastyczność .

Idealnie byłoby, gdyby punkty na wykresie resztowym były losowo rozproszone wokół wartości zero, bez wyraźnego wzoru.

Jeśli napotkasz wykres resztkowy, na którym punkty wykresu mają zakrzywiony wzór, prawdopodobnie oznacza to, że model regresji określony dla danych jest nieprawidłowy.

W większości przypadków oznacza to, że próbowałeś dopasować model regresji liniowej do zbioru danych, który zamiast tego podąża za trendem kwadratowym.

Poniższy przykład pokazuje, jak w praktyce interpretować (i korygować) zakrzywiony wykres reszt.

Przykład: Interpretacja zakrzywionego wykresu reszt

Załóżmy, że zbieramy następujące dane dotyczące liczby godzin przepracowanych tygodniowo i zgłaszanego poziomu szczęścia (w skali od 0 do 100) dla 11 różnych osób w biurze:

Gdybyśmy stworzyli prosty wykres rozrzutu godzin przepracowanych w funkcji poziomu szczęścia, wyglądałoby to tak:

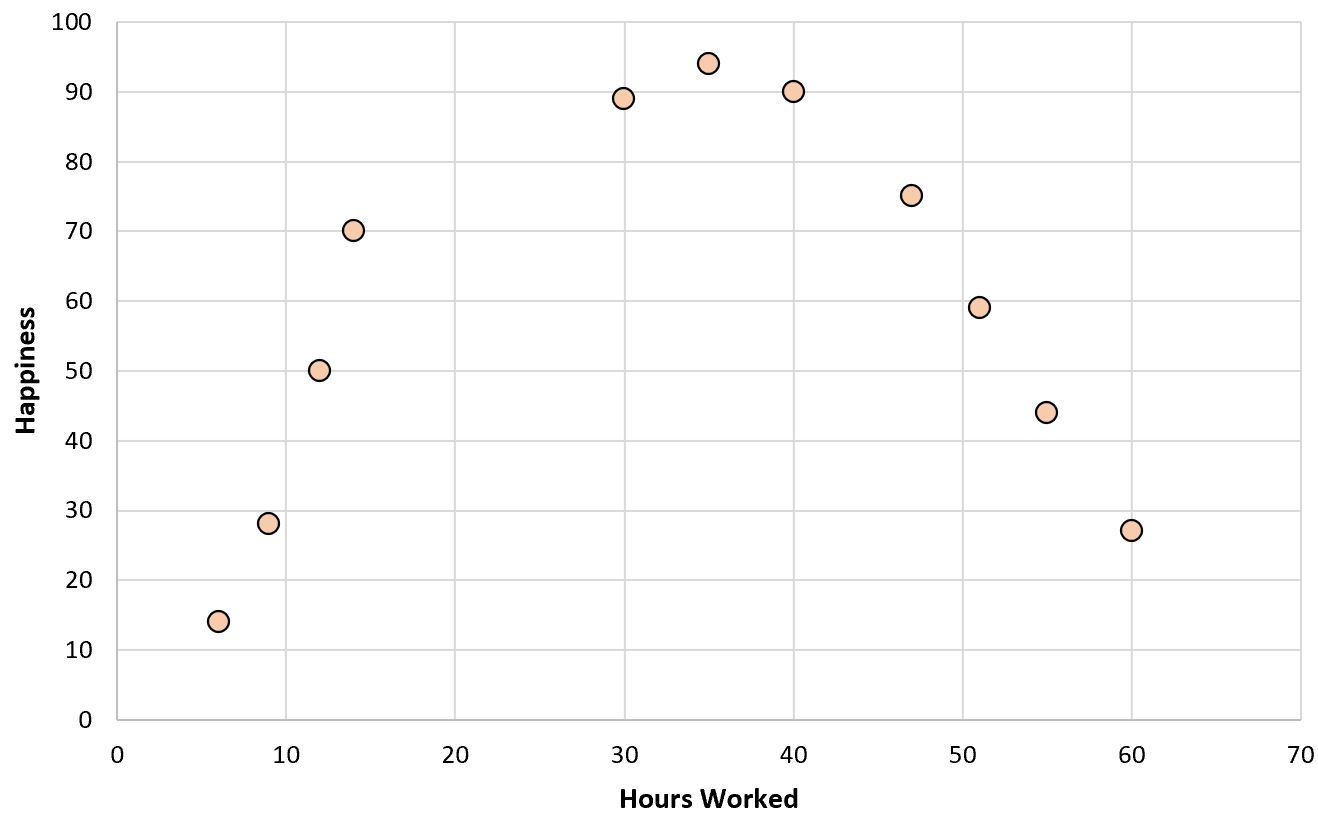
Załóżmy teraz, że chcemy dopasować model regresji, wykorzystując przepracowane godziny do przewidywania poziomu szczęścia.

Poniższy kod pokazuje, jak dopasować prosty model regresji liniowej do tego zbioru danych i utworzyć wykres reszt w języku R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

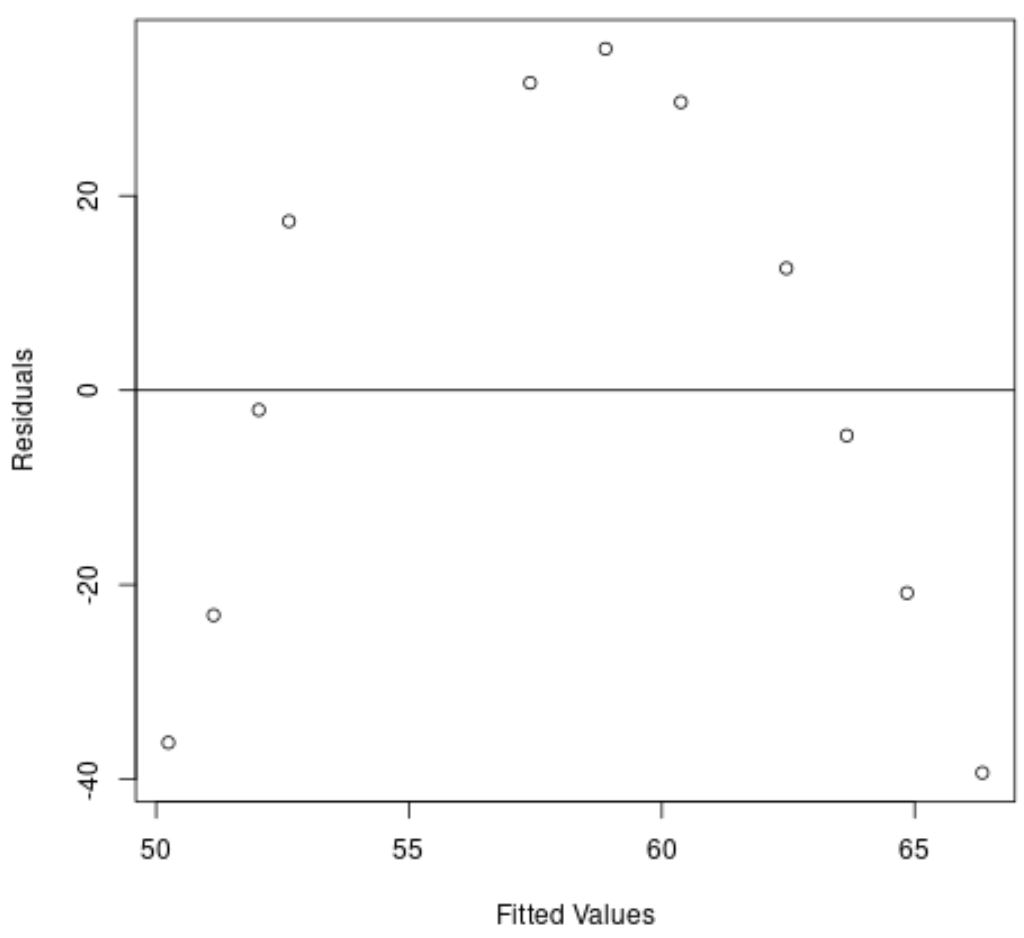
Oś x wyświetla dopasowane wartości, a oś y wyświetla reszty.

Z wykresu widać, że reszty zawierają zakrzywiony wzór, co wskazuje, że model regresji liniowej nie zapewnia odpowiedniego dopasowania do tego zbioru danych.

Poniższy kod pokazuje, jak dopasować model regresji kwadratowej do tego zbioru danych i utworzyć wykres reszt w R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

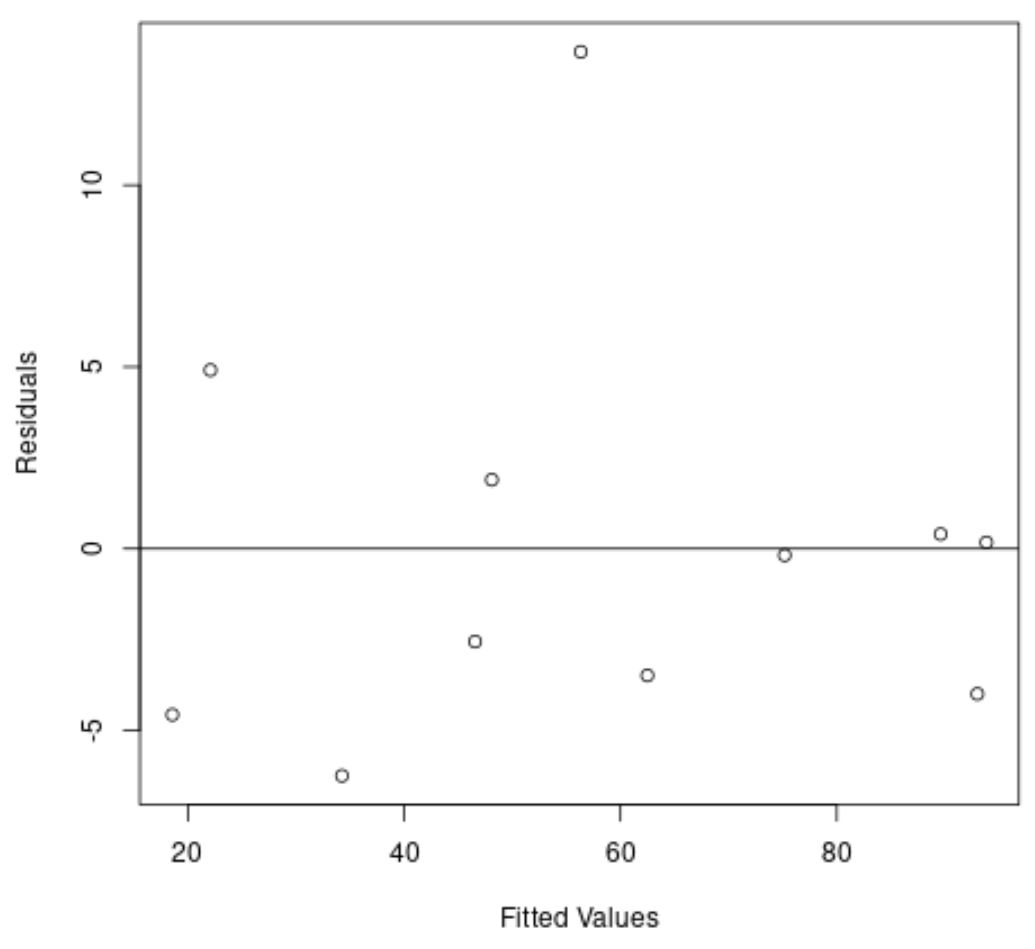
Po raz kolejny oś x pokazuje dopasowane wartości, a oś y pokazuje reszty.

Z wykresu widać, że reszty są losowo rozrzucone wokół zera i nie ma wyraźnego trendu w zakresie reszt.

To mówi nam, że model regresji kwadratowej znacznie lepiej dopasowuje ten zbiór danych niż model regresji liniowej.

Powinno to mieć sens, biorąc pod uwagę, że widzieliśmy, że prawdziwy związek między przepracowanymi godzinami a poziomem szczęścia wydaje się mieć charakter kwadratowy, a nie liniowy.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak tworzyć wykresy reszt przy użyciu różnych programów statystycznych:

Jak ręcznie utworzyć ścieżkę resztkową
Jak utworzyć wykres rezydualny w R
Jak utworzyć wykres resztowy w programie Excel
Jak utworzyć wykres resztkowy w Pythonie