Jak korzystać z funkcji logest w programie excel (z przykładem)

Możesz użyć funkcji LOGEST w programie Excel, aby obliczyć wzór na krzywą wykładniczą pasującą do danych.

Równanie krzywej będzie miało następującą postać:

y = b* ^mx

Ta funkcja wykorzystuje następującą podstawową składnię:

 = LOGEST ( known_y's, [known_x's], [const], [stats] )

Złoto:

• znane_y : tablica znanych wartości y
• znane_x : tablica znanych wartości x
• const : Argument opcjonalny. Jeśli TRUE, stała b jest przetwarzana normalnie. Jeśli FALSE, stała b jest ustawiona na 1.
• statystyki : argument opcjonalny. Jeśli TRUE, zwracane są dodatkowe statystyki regresji. Jeśli FALSE, dodatkowe statystyki regresji nie są zwracane.

Poniższy przykład krok po kroku pokazuje, jak w praktyce wykorzystać tę funkcję.

Krok 1: Wprowadź dane

Najpierw wprowadźmy następujący zestaw danych do Excela:

Krok 2: Wizualizuj dane

Następnie utwórzmy szybki wykres rozrzutu x względem y, aby sprawdzić, czy dane faktycznie układają się po krzywej wykładniczej:

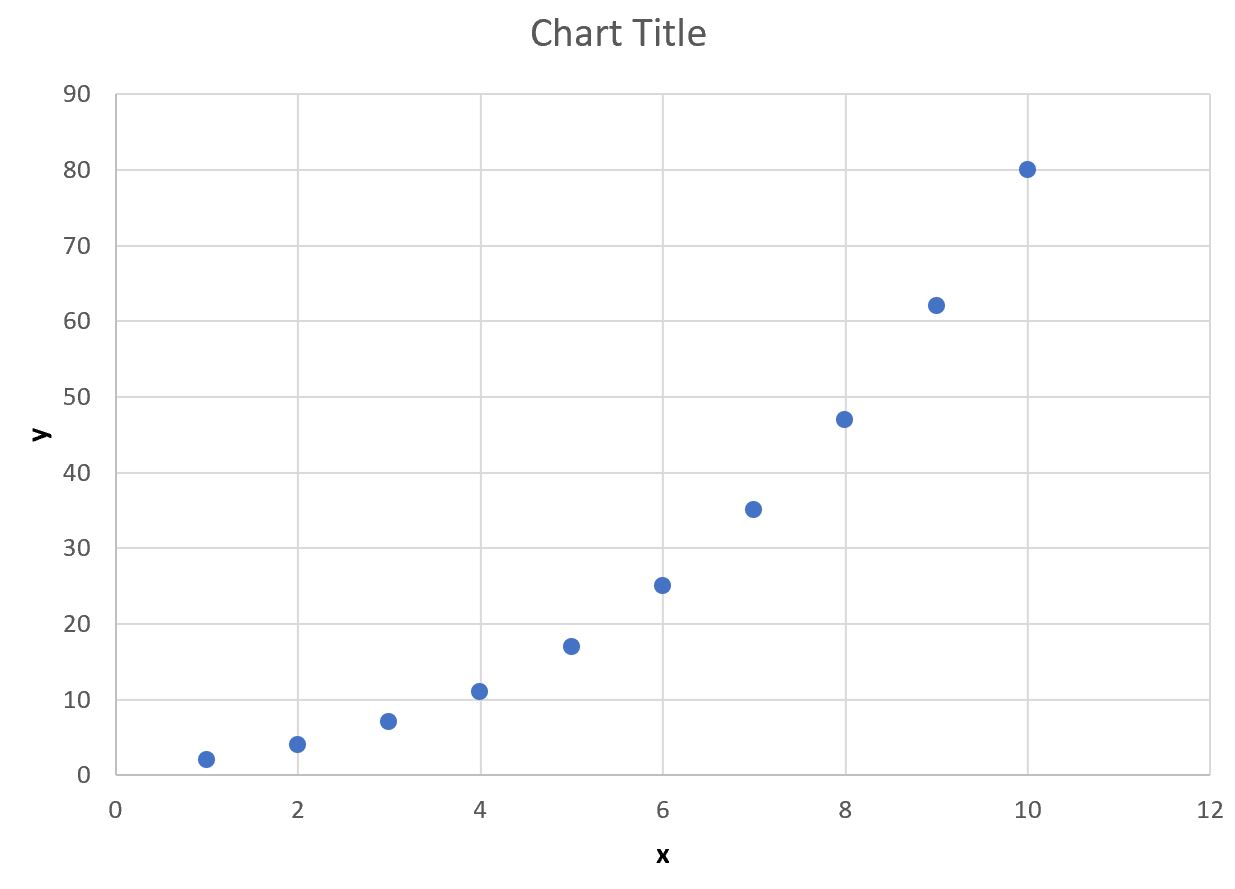
Widzimy, że dane rzeczywiście podążają po krzywej wykładniczej.

Krok 3: Użyj LOGEST, aby znaleźć wzór na krzywą wykładniczą

Następnie możemy wpisać następującą formułę w dowolnej komórce, aby obliczyć formułę krzywej wykładniczej:

 =LOGEST( B2:B11 , A2:A11 )

Poniższy zrzut ekranu pokazuje, jak zastosować tę formułę w praktyce:

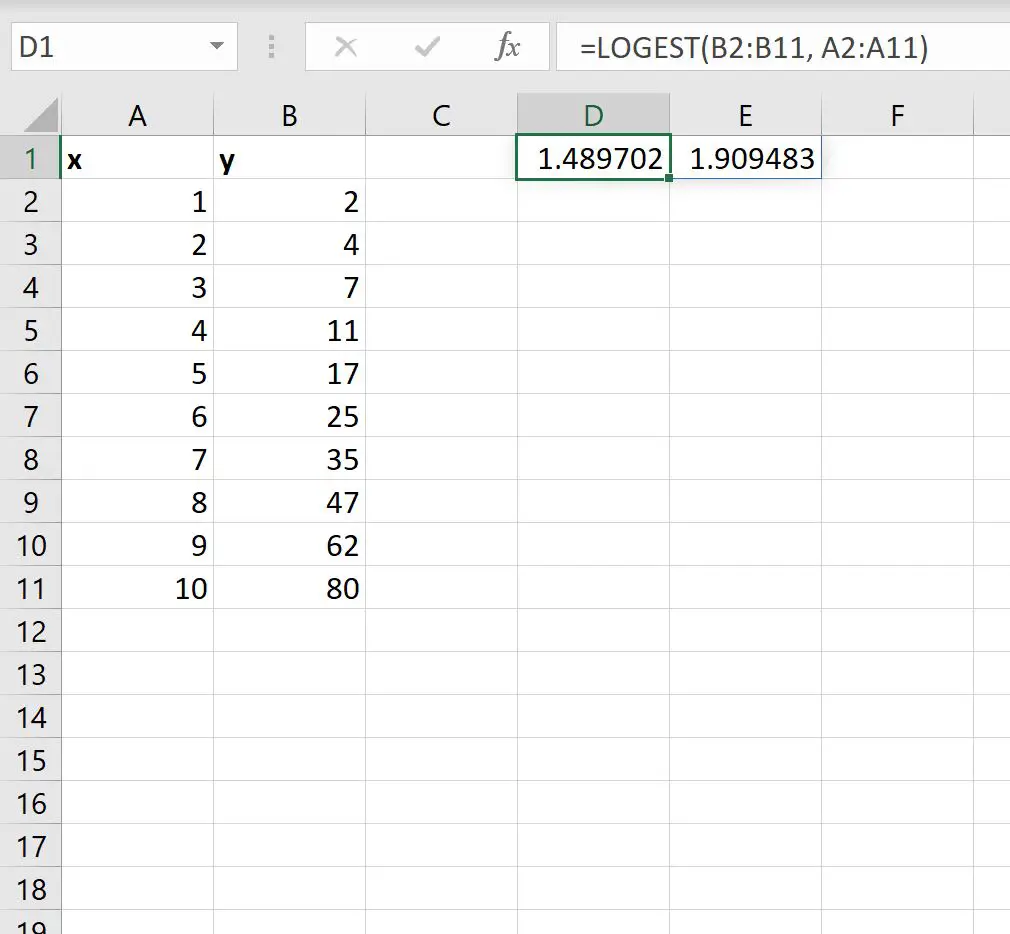
Pierwsza wartość wyniku reprezentuje wartość m , a druga wartość wyniku reprezentuje wartość b w równaniu:

y = b* ^mx

Zapisalibyśmy więc ten wzór na krzywą wykładniczą w następujący sposób:

y = 1,909483 * ^1,489702x

Moglibyśmy następnie użyć tego wzoru do przewidzenia wartości y na podstawie wartości x.

Na przykład, jeśli xa ma wartość 8, to przewidujemy, że y ma wartość 46,31 :

y = 1,909483 * 1,489702 ⁸ = 46,31

Krok 4 (opcjonalnie): Wyświetl dodatkowe statystyki regresji

Możemy ustawić wartość argumentu stats w funkcji LOGEST na PRAWDA , aby wyświetlić dodatkowe statystyki regresji dla dopasowanego równania regresji:

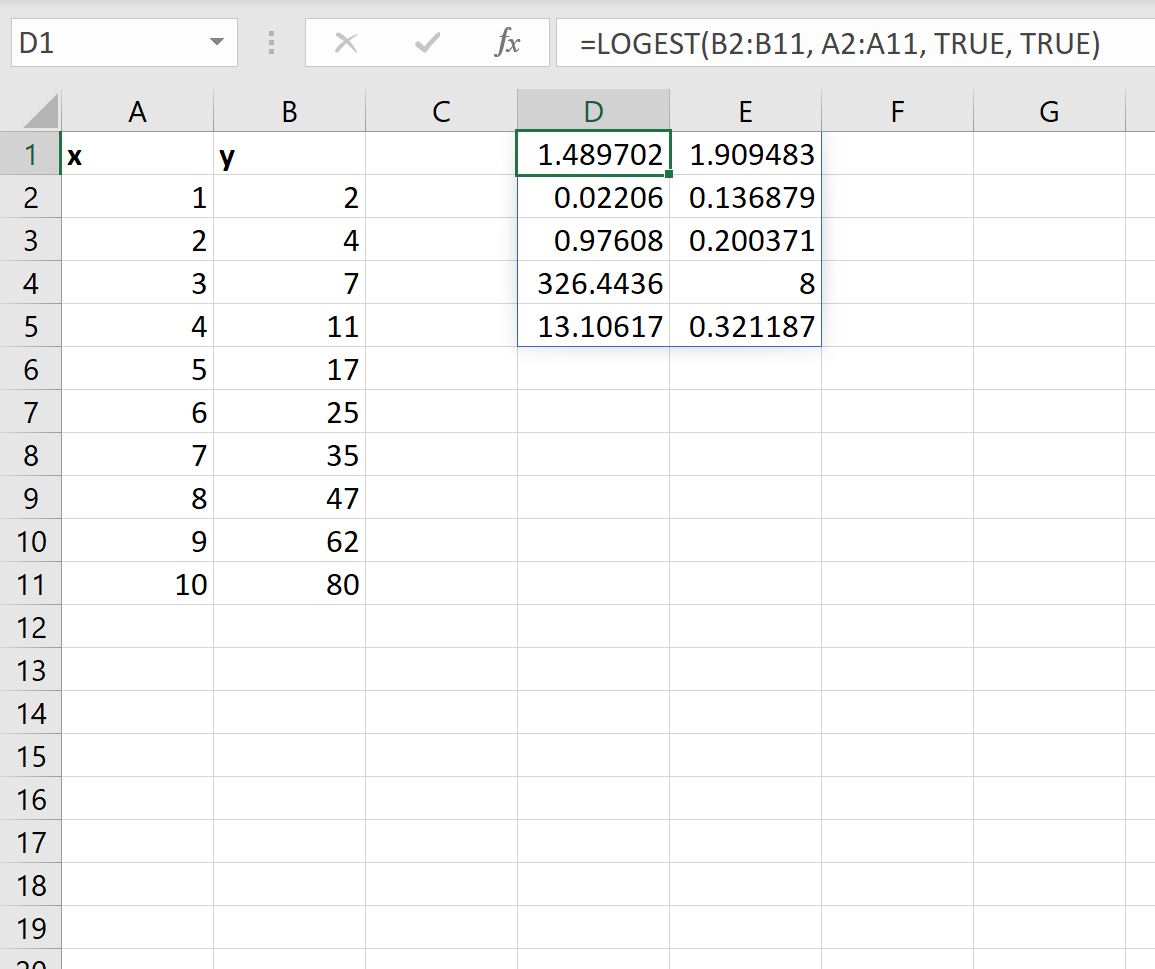
Oto jak interpretować każdą wartość w wyniku:

• Standardowy błąd dla m wynosi 0,02206 .
• Błąd standardowy dla b wynosi 0,136879 .
• R ² modelu to .97608 .
• Standardowy błąd dla y to .200371 .
• Statystyka F to 326,4436 .
• Stopnie swobody wynoszą 8 .
• Suma kwadratów regresji wynosi 13,10617 .
• Pozostała suma kwadratów wynosi 0,321187 .

Ogólnie rzecz biorąc, miarą cieszącą się największym zainteresowaniem w tych dodatkowych statystykach jest wartość ^R2 , która reprezentuje proporcję wariancji zmiennej odpowiedzi, którą można wyjaśnić zmienną predykcyjną.

Wartość ^R2 może zmieniać się od 0 do 1.

Ponieważ R ² tego konkretnego modelu jest bliskie 1, mówi nam to, że zmienna predykcyjna x dobrze przewiduje wartość zmiennej odpowiedzi y.

Powiązane: Jaka jest dobra wartość R-kwadrat?

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje w programie Excel:

Jak korzystać z DEVSQ w Excelu
Jak korzystać z SUMSQ w Excelu
Jak wykonać regresję nieliniową w programie Excel