Cztery założenia regresji liniowej

Regresja liniowa to przydatna metoda statystyczna, którą możemy zastosować do zrozumienia związku między dwiema zmiennymi, x i y. Jednak przed wykonaniem regresji liniowej musimy najpierw upewnić się, że spełnione są cztery założenia:

1. Zależność liniowa: Istnieje liniowa zależność pomiędzy zmienną niezależną x i zmienną zależną y.

2. Niezależność: Reszty są niezależne. W szczególności nie ma korelacji pomiędzy kolejnymi resztami w danych szeregów czasowych.

3. Homoscedastyczność: reszty mają stałą wariancję na każdym poziomie x.

4. Normalność: Reszty modelu mają rozkład normalny.

Jeśli jedno lub więcej z tych założeń nie zostanie spełnione, wyniki naszej regresji liniowej mogą być niewiarygodne lub nawet mylące.

W tym artykule wyjaśniamy każde założenie, wyjaśniamy, jak ustalić, czy założenie jest spełnione i co zrobić, jeśli założenie nie jest spełnione.

Hipoteza 1: Zależność liniowa

Wyjaśnienie

Pierwszym założeniem regresji liniowej jest to, że istnieje liniowa zależność pomiędzy zmienną niezależną x i zmienną niezależną y.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia, czy to założenie jest spełnione, jest utworzenie wykresu rozrzutu x względem y. Pozwala to wizualnie sprawdzić, czy istnieje liniowa zależność między dwiema zmiennymi. Jeśli okaże się, że punkty na wykresie mogą leżeć na linii prostej, wówczas istnieje pewien rodzaj liniowej zależności pomiędzy obiema zmiennymi i założenie to jest spełnione.

Na przykład punkty na poniższym wykresie wydają się układać na linii prostej, co wskazuje, że istnieje liniowa zależność pomiędzy x i y:

Jednakże na poniższym wykresie nie wydaje się, aby istniała liniowa zależność pomiędzy x i y:

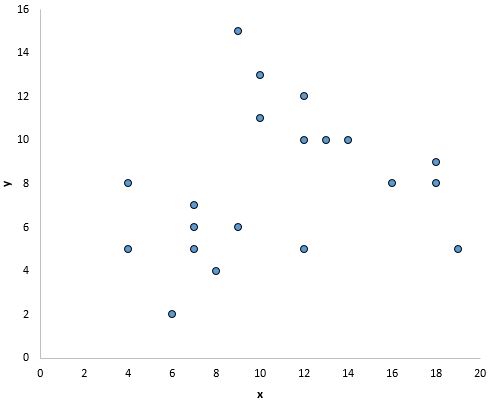
Na tym wykresie wydaje się, że istnieje wyraźna zależność między x i y, ale nie jest to zależność liniowa :

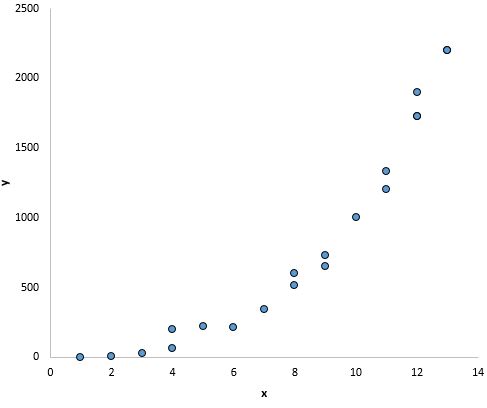
Co zrobić, jeśli to założenie nie jest przestrzegane

Jeśli utworzysz wykres rozrzutu wartości x i y i stwierdzisz, że nie ma liniowej zależności między dwiema zmiennymi, masz kilka opcji:

1. Zastosuj transformację nieliniową do zmiennej niezależnej i/lub zależnej. Typowe przykłady obejmują logarytm, pierwiastek kwadratowy lub odwrotność zmiennej niezależnej i/lub zależnej.

2. Dodaj do modelu kolejną zmienną niezależną. Na przykład, jeśli wykres x względem y ma kształt paraboliczny, sensowne może być dodanie X ² jako dodatkowej zmiennej niezależnej w modelu.

Hipoteza 2: Niepodległość

Wyjaśnienie

Kolejnym założeniem regresji liniowej jest to, że reszty są niezależne. Jest to szczególnie istotne podczas pracy z danymi szeregów czasowych. W idealnym przypadku nie chcielibyśmy, aby wśród kolejnych reszt występował trend. Na przykład pozostałości nie powinny stale wzrastać w czasie.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia, czy to założenie jest prawdziwe, jest przyjrzenie się wykresowi reszt szeregów czasowych, który jest wykresem reszt w funkcji czasu. W idealnym przypadku większość autokorelacji resztowych powinna mieścić się w 95% przedziałach ufności wokół zera, które znajdują się w przybliżeniu +/- 2 z pierwiastka kwadratowego z n , gdzie n jest wielkością próby. Można także formalnie sprawdzić, czy założenie to jest spełnione, korzystając z testu Durbina-Watsona .

Co zrobić, jeśli to założenie nie jest przestrzegane

W zależności od tego, w jaki sposób naruszone zostanie to założenie, masz kilka opcji:

• Aby uzyskać dodatnią korelację szeregową, należy rozważyć dodanie do modelu opóźnień zmiennej zależnej i/lub niezależnej.
• W przypadku ujemnej korelacji szeregowej upewnij się, że żadna ze zmiennych nie jest nadmiernie opóźniona .
• Aby uzyskać korelację sezonową, rozważ dodanie do modelu manekinów sezonowych.

Hipoteza 3: Homoskedastyczność

Wyjaśnienie

Kolejnym założeniem regresji liniowej jest to, że reszty mają stałą wariancję na każdym poziomie x. Nazywa się to homoskedastycznością . Jeżeli tak nie jest, reszty cierpią na heteroskedastyczność .

Kiedy w analizie regresji występuje heteroskedastyczność, trudno uwierzyć w wyniki analizy. W szczególności heteroskedastyczność zwiększa wariancję szacunków współczynnika regresji, ale model regresji tego nie uwzględnia. To sprawia, że znacznie bardziej prawdopodobne jest, że model regresji będzie twierdził, że składnik modelu jest istotny statystycznie, podczas gdy w rzeczywistości tak nie jest.

Jak ustalić, czy to założenie jest spełnione

Najłatwiejszym sposobem wykrycia heteroskedastyczności jest utworzenie dopasowanego wykresu wartości/reszt .

Po dopasowaniu linii regresji do zbioru danych można utworzyć wykres rozrzutu przedstawiający dopasowane wartości modelu w porównaniu z resztami tych dopasowanych wartości. Poniższy wykres rozrzutu przedstawia typowy wykres dopasowanej wartości w funkcji reszty, w której występuje heteroskedastyczność.

Zwróć uwagę, jak reszty rozprzestrzeniają się coraz bardziej wraz ze wzrostem dopasowanych wartości. Ten kształt „stożka” jest klasycznym znakiem heteroskedastyczności:

Co zrobić, jeśli to założenie nie jest przestrzegane

Istnieją trzy typowe sposoby korygowania heteroskedastyczności:

1. Przekształć zmienną zależną. Typową transformacją jest po prostu pobranie logu zmiennej zależnej. Na przykład, jeśli użyjemy wielkości populacji (zmienna niezależna) do przewidywania liczby kwiaciarni w mieście (zmienna zależna), możemy zamiast tego spróbować użyć wielkości populacji do przewidzenia logarytmu liczby kwiaciarni w mieście. Używanie logu zmiennej zależnej zamiast oryginalnej zmiennej zależnej często powoduje zniknięcie heteroskedastyczności.

2. Zdefiniuj na nowo zmienną zależną. Powszechnym sposobem redefiniowania zmiennej zależnej jest użycie stawki , a nie wartości surowej. Na przykład zamiast używać wielkości populacji do przewidywania liczby kwiaciarni w mieście, możemy użyć wielkości populacji do przewidywania liczby kwiaciarni na mieszkańca. W większości przypadków zmniejsza to zmienność, która naturalnie występuje w większych populacjach, ponieważ mierzymy liczbę kwiaciarni na osobę, a nie samą liczbę kwiaciarni.

3. Zastosuj regresję ważoną. Innym sposobem skorygowania heteroskedastyczności jest zastosowanie regresji ważonej. Ten typ regresji przypisuje wagę każdemu punktowi danych na podstawie wariancji jego dopasowanej wartości. Zasadniczo nadaje to niskie wagi punktom danych o większych wariancjach, zmniejszając ich kwadraty resztowe. Zastosowanie odpowiednich wag może wyeliminować problem heteroskedastyczności.

Hipoteza 4: normalność

Wyjaśnienie

Kolejnym założeniem regresji liniowej jest to, że reszty mają rozkład normalny.

Jak ustalić, czy to założenie jest spełnione

Istnieją dwa popularne sposoby sprawdzenia, czy to założenie jest spełnione:

1. Wizualnie zweryfikuj hipotezę za pomocą wykresów QQ .

Wykres QQ, skrót od wykresu kwantylowo-kwantylowego, to rodzaj wykresu, którego możemy użyć do określenia, czy reszty modelu mają rozkład normalny. Jeżeli punkty na wykresie tworzą w przybliżeniu prostą ukośną, wówczas spełnione jest założenie normalności.

Poniższy wykres QQ przedstawia przykład reszt, które w przybliżeniu odpowiadają rozkładowi normalnemu:

Jednakże poniższy wykres QQ przedstawia przykład przypadku, w którym reszty wyraźnie odbiegają od prostej linii ukośnej, co wskazuje, że nie są zgodne z rozkładem normalnym:

2. Założenie o normalności można także sprawdzić za pomocą formalnych testów statystycznych, takich jak Shapiro-Wilk, Kołmogorow-Smironow, Jarque-Barre lub D’Agostino-Pearson. Należy jednak pamiętać, że testy te są wrażliwe na próbki o dużej wielkości – to znaczy, że często stwierdzają, że reszty nie są normalne, gdy wielkość próbki jest duża. Dlatego często łatwiej jest po prostu użyć metod graficznych, takich jak wykres QQ, aby zweryfikować tę hipotezę.

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeżeli założenie o normalności nie jest spełnione, masz kilka możliwości:

• Najpierw sprawdź, czy wartości odstające nie mają dużego wpływu na rozkład. Jeśli występują jakieś wartości odstające, upewnij się, że są to wartości rzeczywiste, a nie błędy przy wprowadzaniu danych.
• Następnie można zastosować transformację nieliniową do zmiennej niezależnej i/lub zależnej. Typowe przykłady obejmują logarytm, pierwiastek kwadratowy lub odwrotność zmiennej niezależnej i/lub zależnej.

Dalsza lektura:

Wprowadzenie do prostej regresji liniowej
Zrozumienie heteroskedastyczności w analizie regresji
Jak utworzyć i zinterpretować wykres QQ w R