Jak obliczyć odległość gotowania w sas

Odległość Cooka służy do identyfikacji wpływowych obserwacji w modelu regresji.

Wzór na odległość Cooka to:

re _ja = (r _ja ² / p*MSE) * (h _ii / (1-h _ii ) ² )

Złoto:

• r _i jest i- ^tą resztą
• p to liczba współczynników w modelu regresji
• MSE to błąd średniokwadratowy
• h _ii to ^i- wartość dźwigni

Zasadniczo odległość Cooka mierzy, jak bardzo zmienią się wszystkie dopasowane wartości modelu po usunięciu i- ^tej obserwacji.

Im większa wartość odległości Cooka, tym większy wpływ ma dana obserwacja.

Ogólnie rzecz biorąc, każdą obserwację z odległością Cooka większą niż 4/n (gdzie n = liczba obserwacji ogółem) uważa się za mającą duży wpływ.

Poniższy przykład pokazuje, jak obliczyć odległość Cooka dla każdej obserwacji w modelu regresji w SAS-ie.

Przykład: Obliczanie dystansu kucharza w SAS

Załóżmy, że mamy następujący zestaw danych w SAS-ie:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

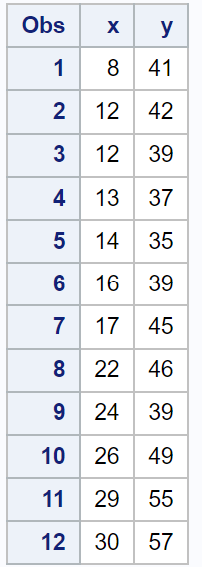
Możemy użyć PROC REG, aby dopasować prosty model regresji liniowej do tego zbioru danych, a następnie użyć instrukcji OUTPUT z instrukcją COOKD , aby obliczyć odległość Cooka dla każdej obserwacji w modelu regresji:

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

Ostateczna tabela wyników wyświetla oryginalny zbiór danych wraz z odległością Cooka dla każdej obserwacji:

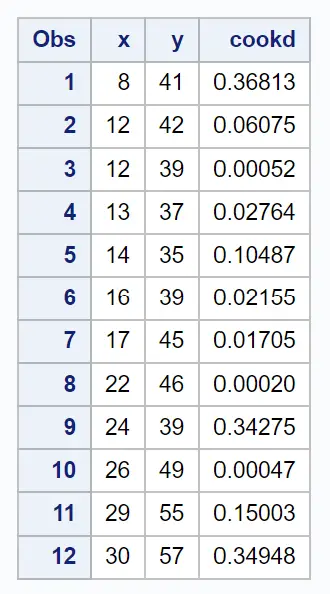
Na przykład możemy zobaczyć:

• Odległość Cooka dla pierwszej obserwacji wynosi 0,36813 .
• Odległość Cooka dla drugiej obserwacji wynosi 0,06075 .
• Odległość Cooka dla trzeciej obserwacji wynosi 0,00052 .

I tak dalej.

Procedura PROC REG również generuje w wynikach kilka wykresów diagnostycznych, na których można zobaczyć wykres odległości Cooka:

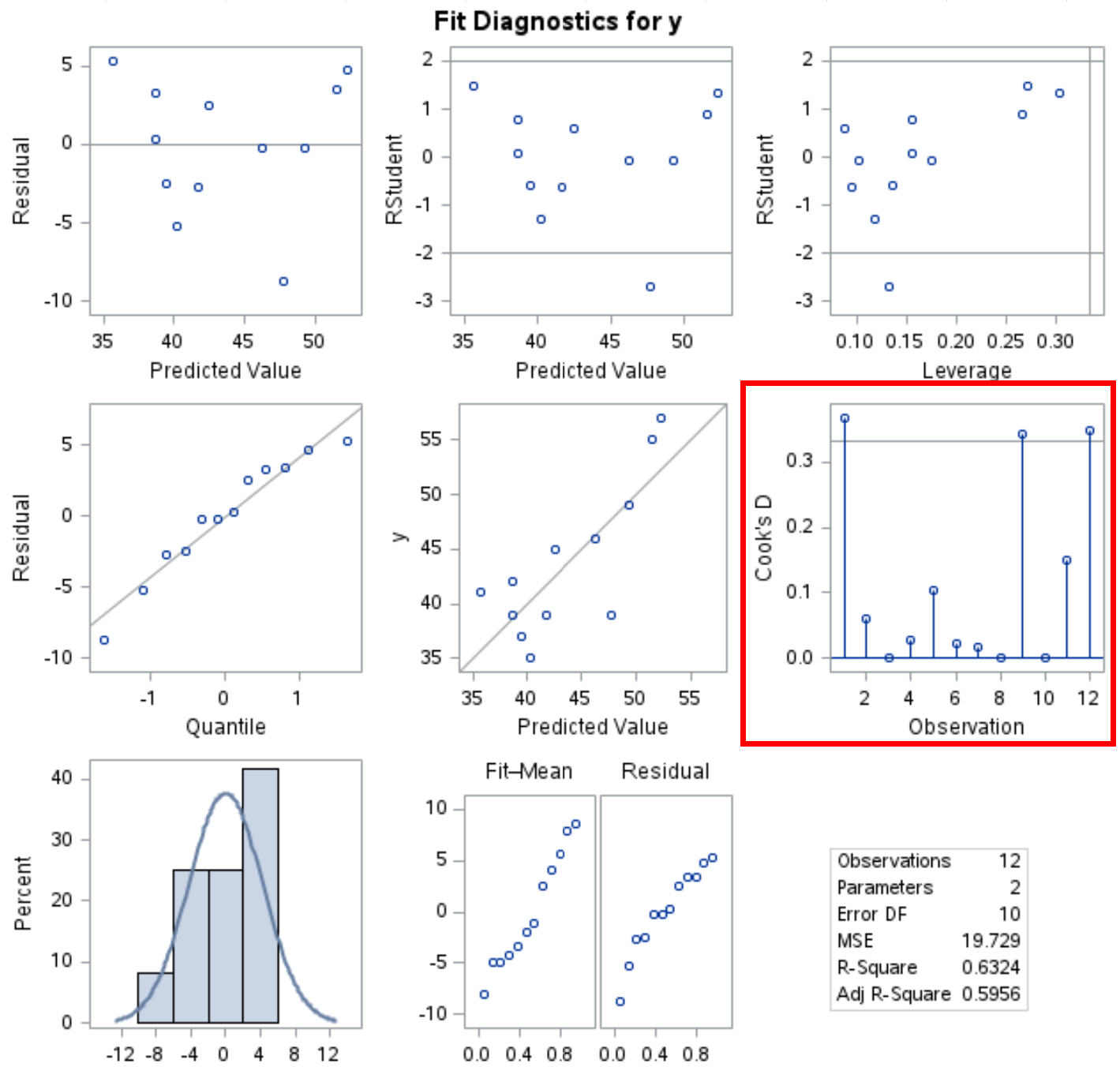
Oś x pokazuje numer obserwacji, a oś y pokazuje odległość Cooka dla każdej obserwacji.

Należy zauważyć, że linia odcięcia znajduje się na poziomie 4/n (w tym przypadku n = 12, więc granica wynosi 0,33) i widzimy, że trzy obserwacje w zbiorze danych są większe od tej linii.

Oznacza to, że obserwacje te mogą mieć duży wpływ na model regresji i być może powinny zostać bliżej zbadane przed interpretacją wyników modelu.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak utworzyć działkę resztkową w SAS-ie
Jak tworzyć histogramy w SAS-ie
Jak tworzyć chmury punktów w SAS-ie
Jak zidentyfikować wartości odstające w SAS