Zestaw walidacyjny i zestaw testowy: jaka jest różnica?

Ilekroć dostosowujemy algorytm uczenia maszynowego do zbioru danych, zazwyczaj dzielimy zbiór danych na trzy części:

1. Zbiór uczący : używany do uczenia modelu.

2. Zbiór walidacyjny : używany do optymalizacji parametrów modelu.

3. Zbiór testowy : używany do uzyskania bezstronnego oszacowania ostatecznej wydajności modelu.

Poniższy diagram przedstawia wizualne wyjaśnienie tych trzech różnych typów zbiorów danych:

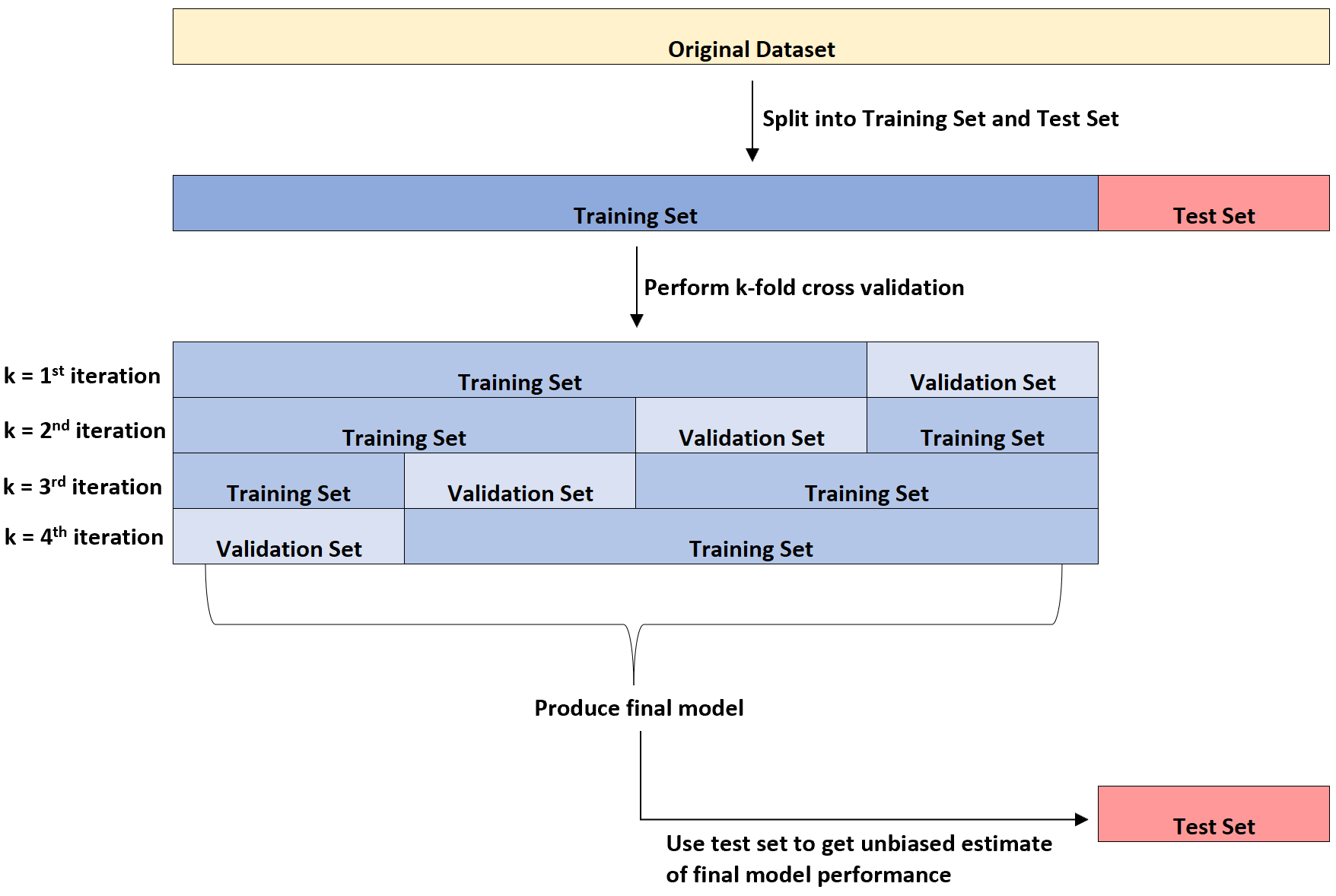
Jednym z punktów zamieszania dla uczniów jest różnica między zbiorem walidacyjnym a zbiorem testowym.

Mówiąc najprościej, zbiór walidacyjny służy do optymalizacji parametrów modelu, podczas gdy zbiór testowy służy do zapewnienia bezstronnego oszacowania ostatecznego modelu.

Można wykazać, że poziom błędu mierzony za pomocą k-krotnej walidacji krzyżowej ma tendencję do niedoszacowania prawdziwego poziomu błędu po zastosowaniu modelu do niewidocznego zbioru danych.

W związku z tym dopasowujemy ostateczny model do zbioru testowego , aby uzyskać bezstronne oszacowanie prawdziwego poziomu błędów w świecie rzeczywistym.

Poniższy przykład ilustruje w praktyce różnicę pomiędzy zbiorem walidacyjnym a zbiorem testowym.

Przykład: Zrozumienie różnicy między zestawem walidacyjnym a zestawem testowym

Załóżmy, że inwestor na rynku nieruchomości chce wykorzystać (1) liczbę sypialni, (2) całkowitą liczbę stóp kwadratowych i (3) liczbę łazienek do przewidzenia ceny sprzedaży danego domu.

Załóżmy, że ma zbiór danych zawierający te informacje na temat 10 000 domów. Najpierw podzieli zbiór danych na zbiór szkoleniowy obejmujący 8000 domów i zbiór testowy obejmujący 2000 domów:

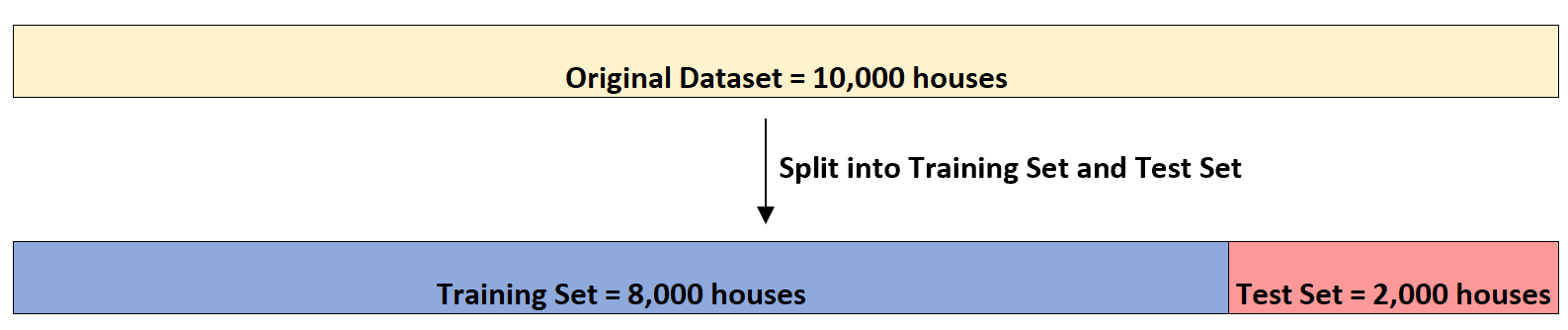
Następnie czterokrotnie dopasuje model regresji liniowej do zbioru danych. Za każdym razem będzie używać 6000 domów w zestawie szkoleniowym i 2000 domów w zestawie walidacyjnym.

Nazywa się to k-krotną walidacją krzyżową.

Zbiór szkoleniowy służy do uczenia modelu, a zbiór walidacyjny służy do oceny wydajności modelu. Za każdym razem do zbioru walidacyjnego będzie używana inna grupa 2000 domów.

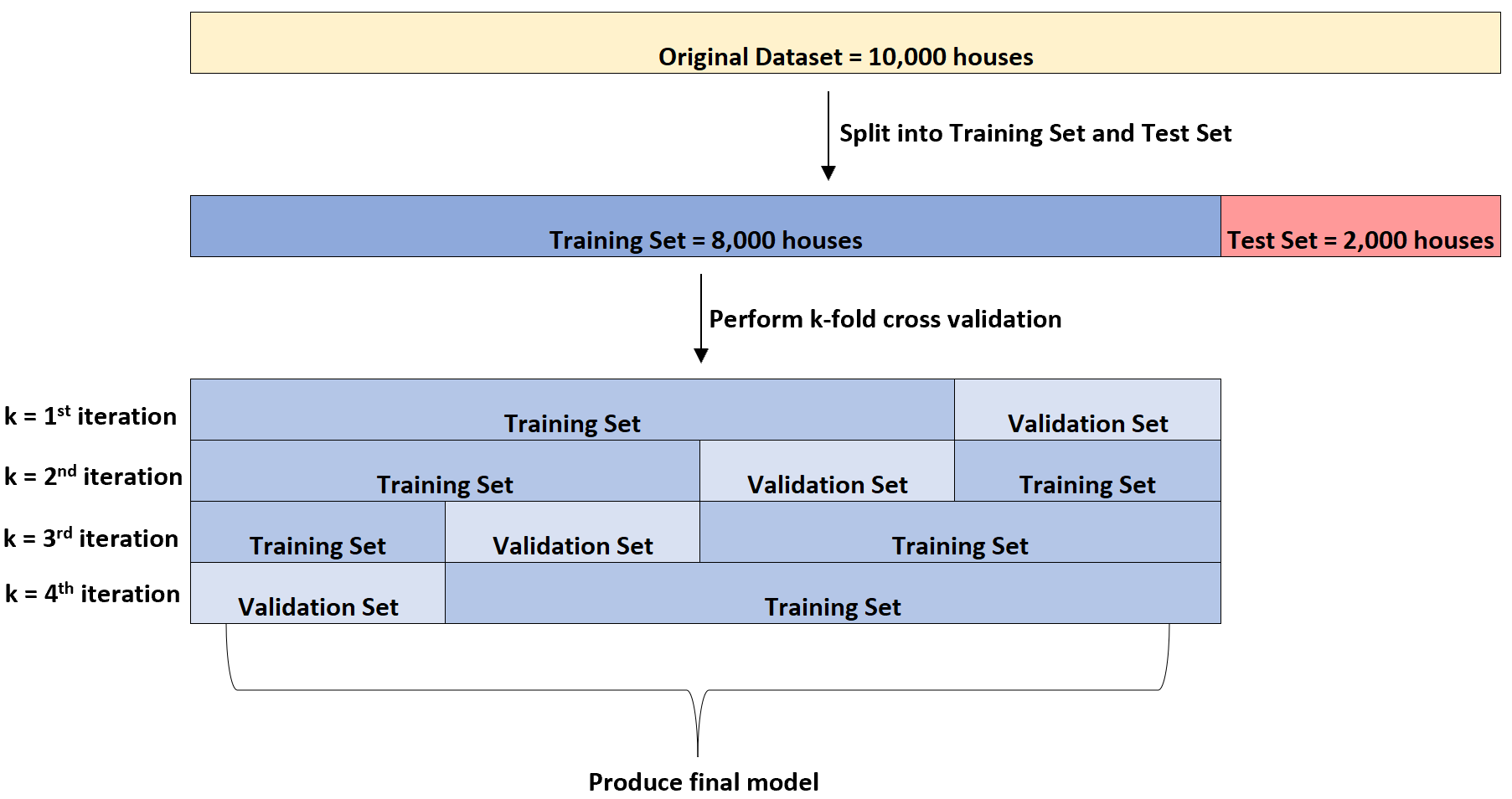
Może przeprowadzić tę k-krotną weryfikację krzyżową na kilku różnych typach modeli regresji, aby zidentyfikować model o najniższym błędzie (tj. zidentyfikować model, który najlepiej pasuje do zbioru danych).

Dopiero po zidentyfikowaniu najlepszego modelu wykorzysta zestaw testowy obejmujący 2000 domów, który zaprezentowano na początku, aby uzyskać bezstronne oszacowanie ostatecznej wydajności modelu.

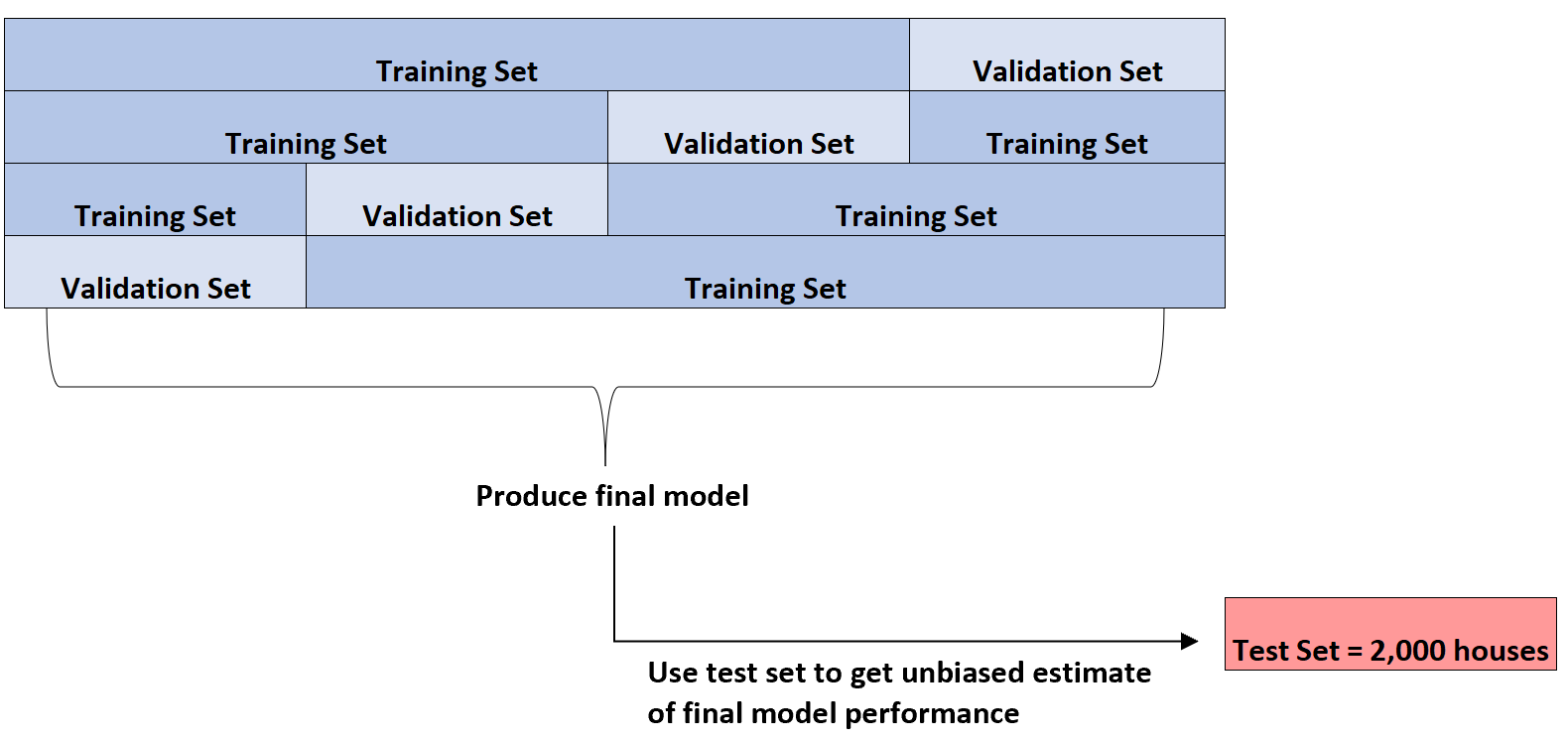
Może na przykład zidentyfikować konkretny typ modelu regresji, którego średni błąd bezwzględny wynosi 8,345 . Oznacza to, że średnia bezwzględna różnica między przewidywaną ceną mieszkania a rzeczywistą ceną mieszkania wynosi 8345 USD.

Następnie może dopasować ten dokładny model regresji do zestawu testowego obejmującego 2000 domów, który nie został jeszcze wykorzystany, i stwierdzić, że średni błąd bezwzględny modelu wynosi 8,847 .

Zatem bezstronne oszacowanie prawdziwego średniego błędu bezwzględnego modelu wynosi 8847 USD.

Dodatkowe zasoby

Prosty przewodnik po walidacji krzyżowej typu K
Jak przeprowadzić weryfikację krzyżową K-Fold w Pythonie
Jak przeprowadzić walidację krzyżową K-Fold w R