Jak interpretować wartości logarytmiczne wiarygodności (z przykładami)

Wartość wiarygodności logarytmicznej modelu regresji jest sposobem pomiaru dobroci dopasowania modelu. Im wyższa wartość logarytmicznej wiarygodności, tym lepiej model pasuje do zbioru danych.

Wartość log wiarygodności dla danego modelu może wahać się od ujemnej nieskończoności do dodatniej nieskończoności. Rzeczywista wartość wiarygodności logarytmicznej dla danego modelu jest na ogół bez znaczenia, ale jest przydatna do porównywania dwóch lub więcej modeli .

W praktyce często dopasowujemy modele regresji wielokrotnej do zbioru danych i wybieramy model o najwyższej wartości logarytmicznej wiarygodności jako model, który najlepiej pasuje do danych.

Poniższy przykład pokazuje, jak w praktyce interpretować wartości logarytmicznego wiarygodności dla różnych modeli regresji.

Przykład: interpretacja wartości logarytmicznego wiarygodności

Załóżmy, że mamy następujący zestaw danych, który pokazuje liczbę sypialni, liczbę łazienek i ceny sprzedaży 20 różnych domów w określonej okolicy:

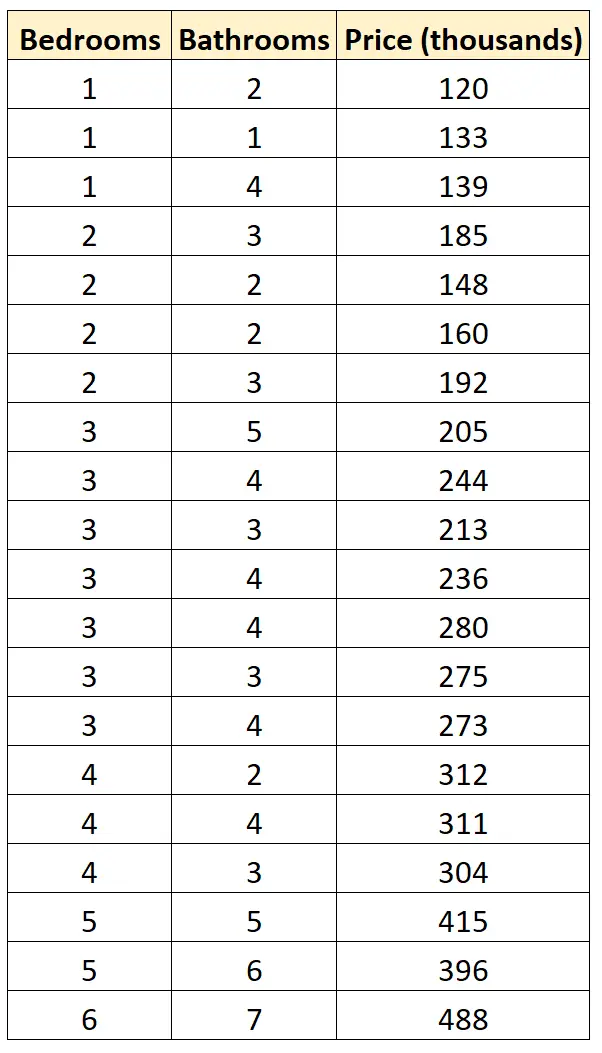
Załóżmy, że chcemy dopasować następujące dwa modele regresji i określić, który zapewnia najlepsze dopasowanie do danych:

Model 1 : Cena = β ₀ + β ₁ (liczba pokoi)

Model 2 : Cena = β ₀ + β ₁ (liczba łazienek)

Poniższy kod pokazuje, jak dopasować każdy model regresji i obliczyć wartość logarytmiczną wiarygodności każdego modelu w R:

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Pierwszy model ma wyższą wartość wiarygodności logarytmicznej ( -91,04 ) niż drugi model ( -111,75 ), co oznacza, że pierwszy model zapewnia lepsze dopasowanie do danych.

Środki ostrożności dotyczące stosowania wartości logarytmicznej wiarygodności

Obliczając wartości wiarygodności logarytmicznej, należy pamiętać, że dodanie do modelu dodatkowych zmiennych predykcyjnych prawie zawsze zwiększy wartość wiarygodności logarytmicznej, nawet jeśli dodatkowe zmienne predykcyjne nie są istotne statystycznie.

Oznacza to, że wartości wiarygodności logarytmicznej należy porównywać tylko pomiędzy dwoma modelami regresji, jeśli każdy model ma tę samą liczbę zmiennych predykcyjnych.

Aby porównać modele z różną liczbą zmiennych predykcyjnych, można przeprowadzić test współczynnika wiarygodności , aby porównać stopień dopasowania dwóch zagnieżdżonych modeli regresji.

Dodatkowe zasoby

Jak używać funkcji lm() do dopasowania modeli liniowych w R
Jak wykonać test współczynnika wiarygodności w R