Kompletny przewodnik: jak interpretować wyniki anova w sas

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Poniższy przykład pokazuje, jak interpretować wyniki jednokierunkowej analizy ANOVA w SAS.

Przykład: Interpretacja wyników ANOVA w SAS

Załóżmy, że badacz rekrutuje 30 studentów do udziału w badaniu. Studenci są losowo przydzielani do stosowania jednej z trzech metod nauki w celu przygotowania się do egzaminu.

Wyniki egzaminu dla poszczególnych uczniów przedstawiono poniżej:

Do utworzenia tego zbioru danych w SAS-ie możemy użyć następującego kodu:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Następnie użyjemy proc ANOVA do wykonania jednokierunkowej ANOVA:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Uwaga : Użyliśmy wyrażenia średnich wraz z opcjami tukey i cldiff , aby określić, że należy przeprowadzić test post-hoc Tukeya (z przedziałami ufności), jeśli ogólna wartość p z jednoczynnikowej analizy ANOVA jest statystycznie istotna.

Najpierw przyjrzymy się tabeli ANOVA w wyniku:

Oto jak interpretować każdą wartość na wyjściu:

Model DF: Stopnie swobody dla metody zmiennej. Oblicza się to jako #grupy -1. W tym przypadku istniały 3 różne metody badawcze, więc ta wartość wynosi: 3-1 = 2 .

Błąd DF: stopnie swobody reszt. Oblicza się to jako #obserwacje ogółem – #grupy. W tym przypadku były 24 obserwacje i 3 grupy, zatem wartość ta wynosi: 24-3 = 21 .

Suma skorygowana : suma modelu DF i błędu DF. Ta wartość to 2 + 21 = 23 .

Model sumy kwadratów: Suma kwadratów powiązana z metodą zmiennej. Ta wartość wynosi 175,583 .

Błąd sumy kwadratów: Suma kwadratów związanych z resztami lub „błędami”. Ta wartość wynosi 350,25 .

Skorygowana suma kwadratów ogółem : Suma modelu SS i błędu SS. Ta wartość to 525,833 .

Model średnich kwadratów: średnia suma kwadratów związana z metodą . Oblicza się to jako model SS / model DF lub 175,583 / 2 = 87,79 .

Błąd średniokwadratowy: średnia suma kwadratów związanych z resztami. Oblicza się to jako błąd SS/błąd DF, który wynosi 350,25/21 = 16,68 .

Wartość F: Ogólna statystyka F modelu ANOVA. Oblicza się to jako średni błąd kwadratowy/średni kwadratowy modelu lub 87,79/16,68 = 5,26 .

Pr >F: Wartość p powiązana ze statystyką F z licznikiem df = 2 i mianownikiem df = 21. W tym przypadku wartość p wynosi 0,0140 .

Najważniejszą wartością w zestawie wyników jest wartość p, ponieważ mówi nam, czy istnieje istotna różnica w wartościach średnich pomiędzy trzema grupami.

Przypomnijmy, że jednokierunkowa analiza ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ (hipoteza zerowa): wszystkie średnie grupowe są równe.
• H _A (hipoteza alternatywna): Przynajmniej jedna średnia grupowa różni się od pozostałych.

Ponieważ wartość p w naszej tabeli ANOVA (0,0140) jest mniejsza niż 0,05, odrzucamy hipotezę zerową.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że średni wynik egzaminu nie jest równy w przypadku trzech metod badawczych.

Aby dokładnie określić, które średnie grupowe są różne, należy odwołać się do tabeli wyników końcowych, która przedstawia wyniki testów post-hoc Tukeya:

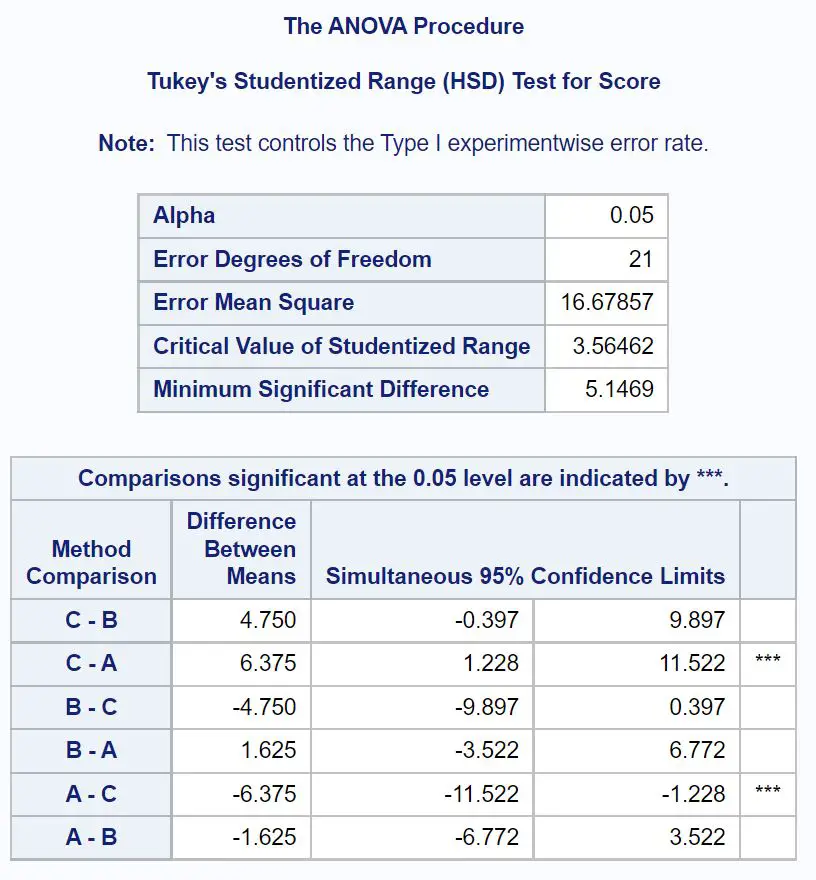
Aby dowiedzieć się, które średnie grupowe są różne, musimy sprawdzić, które porównania parami mają obok siebie gwiazdki ( *** ).

Z tabeli wynika, że istnieje statystycznie istotna różnica w średnich wynikach egzaminów pomiędzy grupą A i grupą C.

W szczególności średnia różnica w wynikach egzaminów pomiędzy grupą C i grupą A wynosi 6,375 .

95% przedział ufności dla średniej różnicy wynosi [1,228, 11,522] .

Nie ma istotnych statystycznie różnic pomiędzy średnimi pozostałych grup.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji o modelach ANOVA:

Przewodnik po korzystaniu z testów post-hoc z ANOVA
Jak wykonać jednokierunkową ANOVA w SAS
Jak wykonać dwukierunkową ANOVA w SAS